PhysicsBoi1908
- 50
- 12
- Homework Statement
- A cylinder P of radius r[SUB]p[/SUB] is being rotated at a constant angular velocity ω[SUB]p[/SUB] with the help of a motor about its axis that is fixed. Another cylinder Q of radius r[SUB]q[/SUB] Free to rotate about its axis that is also fixed is touched with and pressed on P making angle θ between their axes. Soon after the cylinders are pressed against each other, a steady state is reached and cylinder Q acquires a constant angular velocity. Find the final angular velocity of Q and comment on frictional force.
- Relevant Equations
- v= ωr
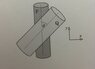
A single pair of points will be in contact between P and Q. The frictional force will try to make the velocity of these points equal.
Say the final angular velocity of Q is ωq.
The velocity of points in contact can never be equal because of difference in directions of ωq and ωp. If I break ωqrq into horizontal and vertical components though, then I can write that its horizontal component must be equal to ωprp.
Thus
ωqrqcosθ=ωprp
And so we get ωq to be:
ωq=-ω_pr_p/r_qcosθ(sinθi+cosθj)
<br />
Which is wrong. The correct answer is:<br />
<div style="text-align: center">ω<sub>q</sub>=-ω<sub>p</sub>r<sub>p</sub>cosθ/r<sub>q</sub>(sinθi+cosθj)​</div><br />
It seems that I was supposed to break ω<sub>p</sub>r<sub>p</sub> into components instead. But I don't see why I should've done that.
Last edited: