Understanding Voltage Distribution in AC Circuits

[phantomvommand]

Homework Statement

This is the electricity problem from 1983 IPhO. I am confused about a small part of the answer, and understand the rest of the solution, so you guys do not have to go through the entire solution. I am only asking about part b.

Relevant Equations

Q = CV,
Kirchoff's laws

The problem is shown below: (I am only asking about part b)

^Above is the problem.

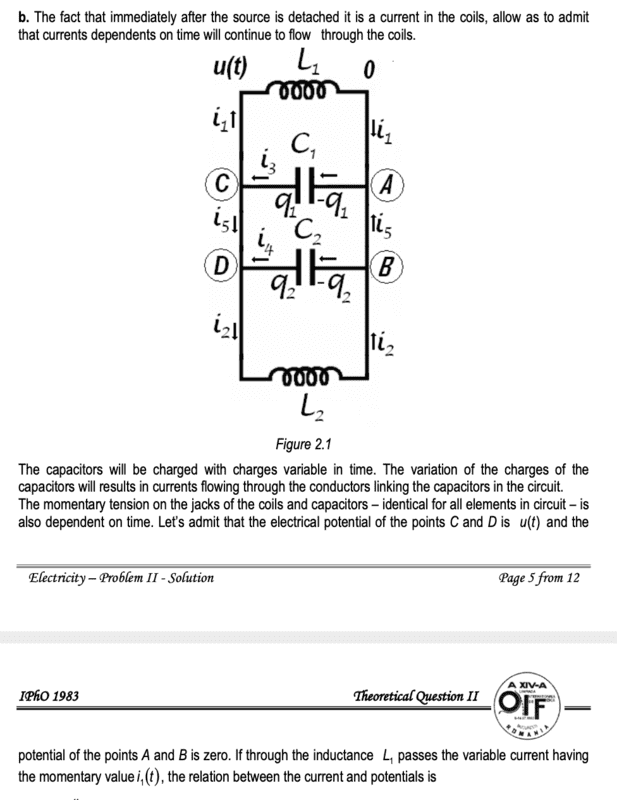
Below is the solution to part b. They have claimed that we can set potential at C = D = u(t), and A=B=0. Why is this claim true?

What I realize:
By applying Kirchoff's across ACDB, Voltage across C1 = Voltage across C2. But the claim that Voltage at C = Voltage at D seems impossible to me. How can there still be a current flowing through CD (denoted by i5), if Vc = Vd? Likewise, how can i5 exist between AB if Va = Vb = 0?

You may refer to the full solution here: https://www.jyu.fi/tdk/kastdk/olympiads/problems.html#83prob (if I have not given enough context).

Thank you!

 

[Delta2]

Thanks for posting a problem from a beautiful era, the era of my youth. 80s were the best era of my life.
Now for your question:
We can have any current between two points A and B as long as the resistance between the two points is zero. By Ohm's law we ll have $$V_{AB}=R_{AB}I_{AB}=0I_{AB}=0\Rightarrow V_A-V_B=0\Rightarrow V_A=V_B$$

 

[phantomvommand]

thanks for this... I must have been so confused :<