Bolter
- 262
- 31
- Homework Statement
- See below
- Relevant Equations
- volume flow rate = vA
Made an attempt at this Q but I'm unsure on how to do part c) or if I had even done part a) and b) right
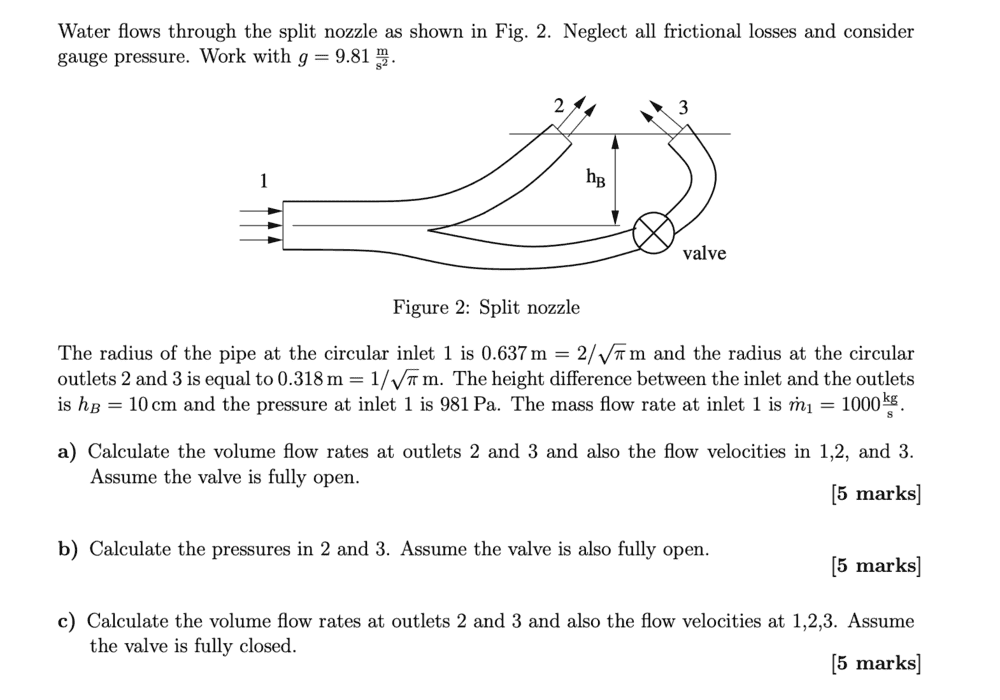

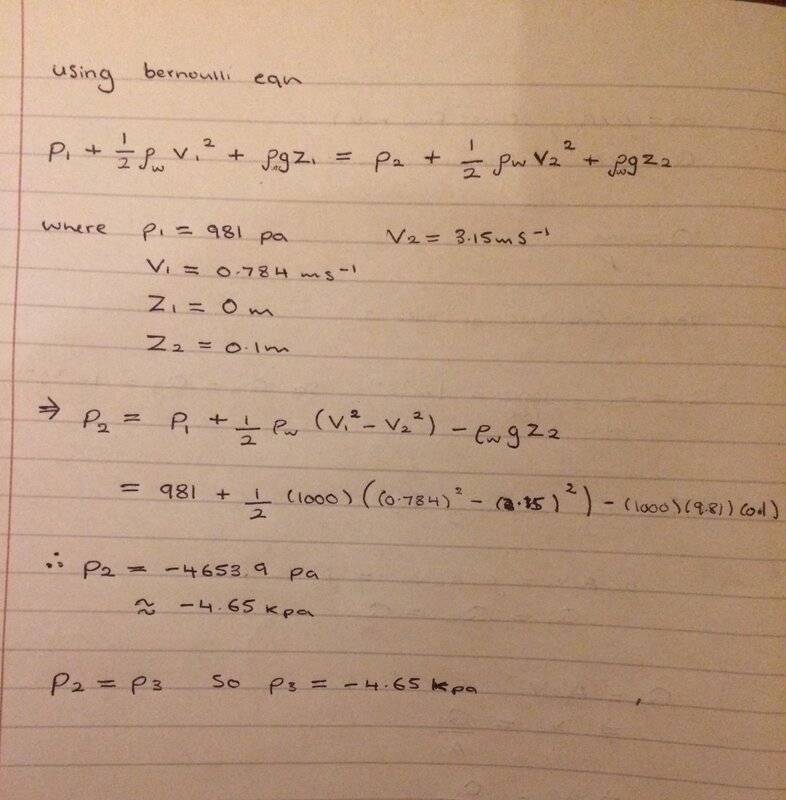
What difference does it make to the volume flow rate equation when the valve goes from open to closed?
Any help would be appreciated! Thanks
What difference does it make to the volume flow rate equation when the valve goes from open to closed?
Any help would be appreciated! Thanks