I started a response to the OP, but it went off in a math-linguistic direction while I was still drawing my diagrams of wheel bolts!
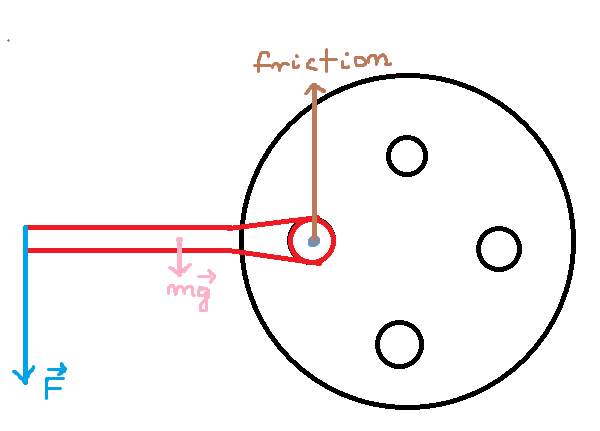
What bothered me about the original post, was the F arrow - not because I didn't think there should be a force there in that direction, nor because I thought there should be a torque or couple or moment. But friction always opposes movement between two objects in contact and I couldn't see any relative movement at that point.
I can see that the downward force on the wrench, applied to the bolt, is trying to move the bolt down. But I thought that force would be opposed, upto more than anything you are likely to apply, by the vertical reaction of the hub. Even if the hub did rotate, say because the wheel slipped, the bolt and its housing would move together. The force through the centre of the bolt perpendicular to the hub radius would still be reaction, not friction.
But, of course, it is friction that is stopping the bolt from turning in its housing. So we need to show where this friction occurs.
Despite previous discussion I've shown friction as a number of distinct arrows. It should be understood that friction occurs over the whole of the mating surfaces, so we could have an infinite number of little arrows, all pointing perpendicular to the radius at their point of action. Their sense will, as always with friction, be opposite to the direction of movement, or attempted movement until friction is overcome.
When we have linear (attempted) movement between two surfaces, all the little arrows point in the same direction - again opposite to the (attempted) movement. So the sum of them all is a single large arrow in that direction.
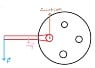
When the (attempted) movement is rotation, every little arrow has an opposite arrow on the other side of the disc, so the sum of all the little arrows is zero! There is no net force in any direction.
But all these little forces DO cause a net torque, moment, couple, or whatever you want to call it, about the centre of rotation.
Each little force multiplied by its radius give a turning force in the same direction, so these sum to a non-zero total.
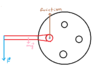
As the previous discussion has said, we can't represent this torque with a single force, but we can represent it with a pair of equal and opposite forces acting at equal and opposite distances from the centre of rotation, ie a couple. (As shown on the left part of the diagram.)
Calculating (the limiting value of) this frictional torque is not quite so easy. I'll leave that* to the excellent mathematicians who've been arguing above.
But we shouldn't need to calculate: If we "torque" it up to 120 Nm when we fit the bolts, presumably that's about the torque we should need to reverse the process.
Here I've shown only the friction between the bolt head and the wheel/hub, but there will also be frictional torque on the threads. Again, since friction is always reactive, this torque will always add to the total frictional torque.
*(Literally on the back of an envelope, I got it to be ##T = \frac {2} {3} \frac {(R^3 - R_0^3)} {(R^2 - R_0^2)} μ F_N##
where ##F_N## is the normal force between the mating surfaces - here the bolt head and the wheel/hub
##μ## the coefficient of friction between these surfaces
##R## is half the outside diameter of the bolt head and ##R_0## half the inside diameter of the bolt head
and T does not include friction elsewhere, such as between the bolt threads and the hub.. )
BTW
russ_watters said:
It's an active topic of discussion in the moderator's forum.
It was a bit rhetorical. I thought most of the participants would have read it. I intended to suggest that some should perhaps bear it in mind when thinking about their contributions here.