Relativity on Rotated Graph Paper (a graphical motivation)

(based on https://www.physicsforums.com/threads/teaching-sr-without-simultaneity.1011051/post-6588952 and https://physics.stackexchange.com/a/689291/148184 )

• In my earlier Insight Spacetime Diagrams of Light Clocks,
  I stated without proof that the areas of all light-clock diamonds are equal.
• In my article, “Relativity on Rotated Graph Paper”, Am. J. Phys. 84, 344 (2016)
  I provided algebraic proof.

In the penultimate draft, I had a non-algebraic motivating argument (which also motivates time dilation and length contraction)
that had to be left out because the article was already too long.

This argument now appears in Introducing relativity on rotated graph paper (Ch 7), my contribution to a recently published book: Teaching Einsteinian Physics in Schools
Kersting and Blair, Routledge 2021, https://doi.org/10.4324/9781003161721
(has supplementary material at the bottom: https://www.routledge.com/Teaching-Einsteinian-Physics-in-Schools-An-Essential-Guide-for-Teachers/Kersting-Blair/p/book/9781003161721 )

The storyline… starting from Einstein’s principles

The storyline goes like this:

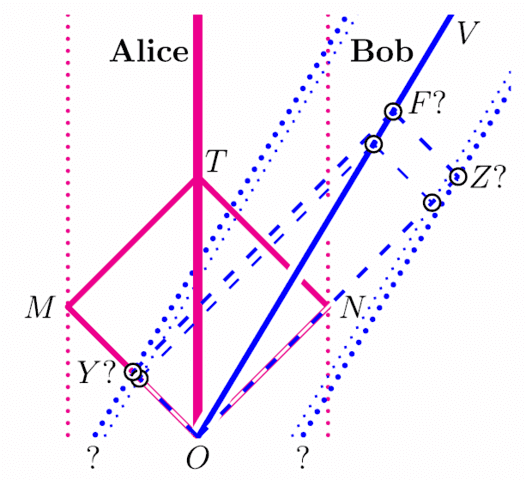
• The Speed of Light Principle and Bob’s Velocity gives the shape of moving observer Bob’s light-clock diamond (with edges parallel to the light cone, to the rotated graph paper).
  • construction:
    Draw Bob’s worldline.
    Bob’s diamonds will have a diagonal along Bob’s worldline and edges parallel to the rotated grid.
    The size of the diamonds corresponds to the spacing of the mirror worldlines, equidistant from and parallel to Bob’s worldline.
    But what determines the size of the clock diamonds? (What event F on Bob’s worldline marks the signal-reflections?)
    

• The Relativity Principle determines the size (the scaling) of Bob’s light-clock diamond.
  (This is what I call the “Calibration Problem”.)
• SIGNAL-EXCHANGE EXPERIMENT: Two inertial observers meet at an event O.
  2 seconds after they meet, they send a signal to the other.
  We expect they have the same results, in accord with the relativity principle.
  (I could have chosen “1 sec”… but the diagram is more cluttered.)

---

An example: the  $v=(3/5)c$ case

• Take $v=(3/5)c$ for simplicity.
  The attempts:

  • Assuming absolute-time… fails the Relativity Principle

    Absolute Time (construct Bob’s diamonds with the same height as Alice’s) fails the Relativity Principle.
    Alice receives at 3.2, but Bob receives at 5.
    Bob’s clock-diamonds have to be larger than these, scaled up (to take longer to tick than Alice’s clock)
    so that Alice receives later (greater than 3.2) on her clock
    and Bob receives earlier (less than 5) on his clock.
    This implies time-dilation… but by how much?
    

  • Assuming absolute-space…fails the Relativity Principle

    Absolute Space (construct Bob’s diamonds with the same cross-section length as Alice’s) fails the Relativity Principle.
    Alice receives at 5, but Bob receives at 3.2.
    Bob’s clock-diamonds have to be smaller than these, scaled-down (so that the cross-section length is shorter than Alice’s)
    so that Alice receives earlier (less than 5) on her clock
    and Bob receives later (greater than 3.2) on his clock.
    This implies length-contraction… but by how much?
    

  • Satisfying the Relativity Principle

    By trial and error (or some analysis*), we are successful.
    Alice and Bob receive at 4.
    We see the Doppler Effect since $k=(4\ \mbox{ticks})/(2\ \mbox{ticks})=2$ (as expected for $v=(3/5)c$ )
    (and equality of light-clock areas [invariance of square-interval]), in accord with Special Relativity.
    Time-Dilation and Length-Contraction and Relativity of Simultaneity are consequences,
    with the correct factors (by counting diamonds along the triangle legs).
    

  [* possible analysis: Since the round-trips are equal in both of the previous cases, we might
  expect the geometric mean $\sqrt{(3.2)(5)}=4$ to be the expected result of their signal-exchange experiment.]

Try this for $v=(4/5)c$.

Play with these using
https://www.geogebra.org/m/HYD7hB9v#material/UBXdQaz4 (make sure BOB’s diamonds are shown)
https://www.geogebra.org/m/kvfsq664 (updated)… (make sure BOB’s diamonds are shown)
[You can manually adjust Bob’s velocity and “lengths [in the lab frame]” of the light clocks.]

To obtain the textbook formula relating the time-dilation factors and relative velocity, we would to proceed along the lines of my AJP article.

But the point is that we can show (with a geometric construction and without algebra) how the Relativity Principle and the Speed of Light Principle imply the incompatibilities with Absolute Time and Absolute Space, and suggest the need for the time-dilation and length-contraction effects (as side-effects), on the way to establishing the equality of light-clock diamond areas (which is essentially the invariance of the square interval).

Further reading:

Relativity on Rotated Graph Paper 
Learn About Relativity on Rotated Graph Paper
Learn About Spacetime Diagrams of Light Clocks