Trick to Solving Integrals Involving Tangent and Secant
This little trick is used for some integration problems involving trigonometric functions is probably well-known, but I only learned it yesterday. So under the assumption that others don’t know it, I will share my insight.
When you take calculus, one of the most mysterious integrals is this one involving the secant:
∫ sec(θ) dθ = log(sec(θ) + tan(θ))
It’s not too hard to prove that it’s true (by taking the derivative of the right side), but how did anyone ever come up with this? And how are you supposed to remember it?
Well, this and related integrals can be solved by a weird substitution involving the hyperbolic trig functions. The most obvious relationship between the trig functions and the hyperbolic trig functions is implied by the names:
sinh(x) ⇒ -i sin(ix)
cosh(x) ⇒ cos(ix)
tanh(x) ⇒ -i tan(ix)
sech(x) ⇒ sec(ix)
But there is a non-obvious relationship that can be seen by looking at the identities, or looking at the graphs:
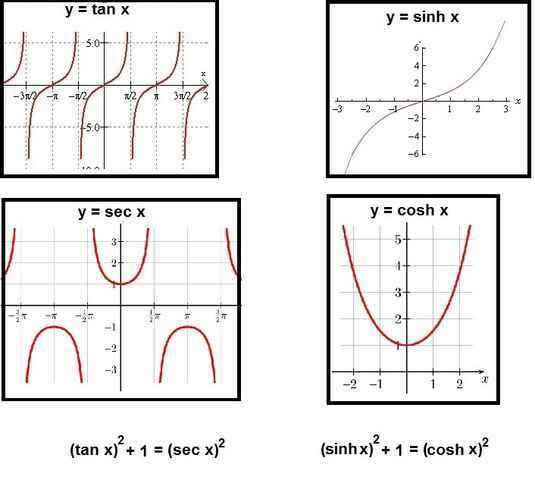
trig and hyperbolic trig functions
The shape of the tangent function on the interval from -π/2 to +π/2 is similar to that of the hyperbolic sine function on the interval from -∞ to +∞. The shape of the secant function is similar to that of the hyperbolic cosine. More importantly, the pair of functions tan and sec share the same identity with sinh and cosh:
(tan x)² + 1 = (sec x)²
(sinh x)² + 1 = (cosh x)²
So these analogies inspire the implicit variable substitution:
tan x → sinh y
We can easily show that
dx/dy = 1/(cosh y)
How does that help? Well, with this substitution:
∫ sec^n(x) dx = ∫ cosh^{n-1}(y) dy
Integrating powers of cosh is pretty straightforward (you can use integration by parts repeatedly). But the simplest case is when n=1. In that case, the integral becomes:
∫ sec(x) dx = ∫ dy = y
Looking back at our definition of y in terms of x, we get the result:
∫ sec(x) dx = arcsinh(tan x)
There’s your answer. Hmm. But the original formula involved log and not arcsinh! Not to worry–they are the same:
- arcsinh(u) = v
- sinh(v) = u
- (e^{v} – e^{-v})/2 = u
- e^{2v} – 2u e^v = 1
- Solving for e^{v} gives e^v = u + √(1+u^2
- So v = log(u + √(1+u^2))
- So arcsinh(u) = log(u + √(1+u^2))
So ∫ sec(x) dx = arcsinh(tan x) = log(tan x + √(1+(tan x)^2) = log(tan x + sec x)





Thanks, useful for my calculus teaching! :)
Very cool Daryl, thanks!
@vanhees71 Awesome, I hadn't seen this one.
I still can't give five stars though.:sorry:
Finally I could give you your 5 stars! :-).
An alternative way to integrate ##sec x## is to use the standard subsitution
$$u=tan left (frac{x}{2} right), quad mathrm{d} x=mathrm{d} u frac{1}{1+u^2}.$$
The integrand is
$$sec x= frac{1}{cos x}=frac{1}{2 cos^2 (x/2)-1}=frac{1-u^2}{1+u^2}.$$
Thus you get
$$int mathrm{d} x sec x= int mathrm{d} u frac{2}{1-u^2} = int mathrm{d} u left (frac{1}{u+1}-frac{1}{u-1} right) = ln left |frac{u+1}{u-1} right|+C$$
or finaly resubstituting
$$int mathrm{d} x sec x=ln left |frac{tan(x/2)+1}{tan(x/2)-1} right|+C.$$
I'd like to give this Insight 5 stars, but it just doesn't let me, because I'm not logged in for some reason when clicking at this specific Insight article. Anyway, it's a great trick, I hope to remember when I need it.
Fascinating!
The most commonly given proof in high school for integrating sec x is multiplying the numerator and denominator by sec x + tan x. To me it seemed like a highly unintuitive step. Integrating sec x by using partial fractions – a longer but more intuitive proof, originally discovered by Barrow is the one I prefer.
This is pretty cool too. Thanks for the insight!