Basic algebra Definition and 52 Threads

Elementary algebra encompasses some of the basic concepts of algebra, one of the main branches of mathematics. It is typically taught to secondary school students and builds on their understanding of arithmetic. Whereas arithmetic deals with specified numbers, algebra introduces quantities without fixed values, known as variables. This use of variables entails use of algebraic notation and an understanding of the general rules of the operators introduced in arithmetic. Unlike abstract algebra, elementary algebra is not concerned with algebraic structures outside the realm of real and complex numbers.
The use of variables to denote quantities allows general relationships between quantities to be formally and concisely expressed, and thus enables solving a broader scope of problems. Many quantitative relationships in science and mathematics are expressed as algebraic equations.

View More On Wikipedia.org
Recent contents Top users
  1. L

    B A question about rules of multiplication

    This might sound like a stupid question but I am just wondering why is it that x times yz equals xyz and not xyxz ? Why don't we distribute multiplication in this case ?
  2. koiuuuuuuuuuuu

    B Is 3x=15 Really That Hard to Solve?

    Can you help me with this question. 3x=15 Do you have to divide both sides by 3 which, is x=5 Am I right. If not explain please, Thank-you
  3. chwala

    Is There a Universal Standard for Order of Operations in Mathematics?

    attempt 1. 6 /2×3 = 3×3=3×3=9 attempt 2 6/2(3)= 6 divide 6 = 1. sorry i cannot see the divide symbol.
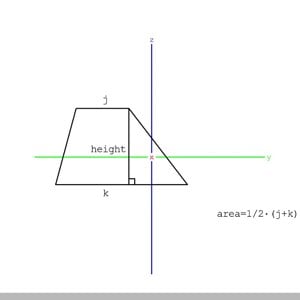
  4. Trapezoid Area Formula Origin

    Trapezoid Area Formula Origin

    How trapezoid's area formula came to be.
    • YoungPhysicist
    • Media item
    • basic algebra trapezoid
    • Comments: 0
    • Category: Basic Algebra
  5. amerikantech

    Linear equation, point slope conversion

    Homework Statement convert: Y − 200 = −4 (X − 15) to X = −0.25 ⋅ Y + 65. with a given Δy/Δx = -36/4 Homework Equations point slope, slope intercept The Attempt at a Solution I understand point slope, slope intercept, and standard form, I understand how to convert one to the other, but I...
  6. D

    B Calculating Rod Speeds with Algebraic Formulas

    I am trying to create a formula for a spreadsheet to calculate values and it has been thirty years since high school algebra. Here are the formulas I need to rearrange. w=(d/r)/t v=d/t w is an unknown constant and I have values for v1 and r1 I need the formula to spit out v2 if I input r2 in...
  7. D

    B Looking for some intuition on a basic Algebra equation

    This isn't for math homework. I'm in self study and came across something in my book that I'm seeking clarification for. The equation: $$0.3\left(50-x\right)=6$$ The solution: $$3\left(50-x\right)=60$$ $$150-3x=60$$ $$-3x=-90$$ $$x=30$$ Simple enough. My question is in regards to this: The...
  8. RabbitWho

    Moving things to the other side of the equals sign

    Homework Statement A 20gram bullet it shot out of a 10kg gun at a speed of 300 m/s What is the recoil speed of the gun (I am putting this in maths rather than physics because I understand the physics part it is just basic maths of using an equation that I am stuck with) Homework Equations G=...
  9. Ghostcrown

    Trouble with basic algebra in Calculus 1.

    It's rather strange, isn't it? I did just fine in Algebra I, and even better in Algebra II, but now that I'm in Calculus I I'm finding that my algebra skills aren't as sharp as I thought they were. Often times i'll get the calculus portions of problems correct, but when it comes down to...
  10. LiHJ

    Can x be written as both a positive and negative value in an equation?

    << Mentor Note -- OP has been advised to type their questions into the forum next time, instead of inserting images >> 1. Homework Statement Dear Mentors and PF helpers, I have a question from today's lesson. Homework EquationsThe Attempt at a Solution Is 1) and 2) both acceptable? If...
  11. R

    Basic Algebra: tan δ = 1/wCR | Confirmation Needed

    please see attached image why has our lecturer put tan δ = 1 / wCR ? if you divide the two equations to get tan wouldn't it be R/wC ? thanks for any conformation
  12. binbagsss

    Index notation/ Tensors, basic algebra questions.

    Ok I have T_{ij}=μS_{ij} + λ δ_{ij}δS_{kk}. I am working in R^3. (I am after S in terms of T) . I multiply by δ_{ij} to attain: δ_{ij}T_{ij}=δ_{ij}μS_{ij} + δ_{ij} λ δ_{ij}δT_{kk} => T_{jj}=δ_{jj}λS_{kk}+μS_{jj} * My question is , for the LH term of * I choose T_{jj} rathen than T_{ii}. I...
  13. F

    MHB Basic Algebra Question: A Diophantine Problem

    The Price of each shirt is 70 dollars and the price of each tie is 30 dollars. He spent a total amount of exactly 810 dollars and bought the maximum number of shirts. What is the ratio of the number of Shirt to Ties? Help Please!Thanks, James
  14. Greg Bernhardt

    Algebra Is Basic Algebra I by Nathan Jacobson Suitable for Self-Study?

    Author: Nathan Jacobson Title: Basic Algebra I Amazon Link: https://www.amazon.com/dp/0486471896/?tag=pfamazon01-20 Prerequisities: Contents:
  15. F

    Basic algebra ex. prob., can't work out a step

    Homework Statement Hi all, I'm not in school, but I am self-studying because I'm helping tutor relatives of mine. The book says at this point, "apply the diagonal rule". I just need a pointer, because I don't know where to go from here. The book contains the answer, and I understand the...
  16. U

    Where Did I Go Wrong in Simplifying this Algebraic Expression?

    Simplify -d^2+[9d+(2-4d^2)] -d^2+[9d+(2-4d^2)] d^2[-9d-2+4d^2] d^2+4d^2-9d-2 5d^2-9d-2 but wolfram says the answer is -5d^2-9d+2 What did I do wrong?
  17. H

    Finding the Capacity of a Jug Using Basic Algebra

    Homework Statement A man had a ten gallon keg of wine and a jug. One day, he drew off a jug full of wine and filled up the keg with water. Later on, when the wine and the water had got thoroughly mixed, he drew off another jugful and again filled up the keg with water. The keg then contained...
  18. 9

    Basic algebra: find break-even point

    Homework Statement Mike make shirts. He has fixed daily costs of $150. It costs an additional $3 to make each shirt. He would like to make a profit of $750 a day making shirts. If he can make 24 shirts a day, how much must he charge to meet his goal? Find break even point. Homework Equations...
  19. V

    Why does the solution for t in the equation Vf=Vi+at result in a negative sign?

    Ok so here is my problem: Vf=Vi+at I want to solve for t so: (Vf-Vi)/a = t right so now my problem starts how can this happen: t = -Vf/a ? The solution above comes from this site http://www.monmsci.net/~fasano/phys1/Chapter_2_10.pdf scroll down to problem 2.31 and you will find what I...
  20. G

    How many arithmetic and basic algebra errors do you make

    when i do higher maths i make a tone of basic algebra and arithmetic mistakes. i was going a basic AX = B using LU decomposition in linear algebra and I had to go back and check my basic math about 6 times before i got the right answer. is it just me or do a lot of people do this?
  21. P

    Squaring both sides of an equation: To include or not to include the minus sign?

    say the i had the equation x -3√x - 16 = 0, if I was to square every term to get rid of the root would it be: 1) x + 9x + 16 = 0 2) x - 9x - 16 = 0 Just confused if I should include the minus sign
  22. N

    A basic algebra question (no calculator)

    Homework Statement Simplify 3√-27x^6 I'm very confused on how to evaluate what -27^(1/3) is without a calculator. I think I'm fine with the other steps. if someone could explain this to me I would really appreciate it. The Attempt at a Solution = 3√-27x^6 = (-27x^6)^(1/3) =...
  23. O

    Understanding and Solving Basic Algebraic Equations

    Hi, I'm having some trouble understanding how to tackle this question, I would appreciate it if some one could enlighten me on how to do this step by step and as in depth as possible. It may seem simple to some, but I am fairly new to this sort of equation. The equation is: −5[−2(m − 3n)...
  24. Femme_physics

    Basic Algebra Simplifying a complex fraction

    This problem comes from an engineering exercise (hence the C/R which you can ignore). I want to see if I got it right. http://img51.imageshack.us/img51/3989/mama1h.jpg http://img851.imageshack.us/img851/3401/mam2.jpg
  25. T

    Basic algebra concept is puzzling me

    basic algebra concept is puzzling me... Homework Statement I don't understand why √10-5 + √5 = 2√5 Could someone please explain this to me real quick...totaly forgot why this is :P Homework Equations none The Attempt at a Solution here I am! thoughts about it and I am still...
  26. A

    How Does Simplifying Quadratic Equations Affect Their Solutions?

    1) When you simplify a quadratic equation (or others) to make it positive or to make the a coefficient equal to 1, do you divide by whatever number you need to make it one or do you factor it out? e.g. 0 = -x^2 + 4x + 21 0 = x^2 - 4x - 21 or 0 = -(x^2 - 4x - 21) 2) When you...
  27. 2

    Why Do Terms in the Energy Equation Not Cancel as Expected?

    I have an equation relating potential energy1 plus gravitational energy1 = potential energy2 plus gravitational energy2 1/2 mv21 + mg1 = 1/2 mv22 + mg2 Now cancelling out the terms I have v21 + 2gy1 + v22 2gy2 Now I don't understand why mg in the second term of both expressions don't cancel...
  28. W

    Mastering Archery Adjustments: Solving for B with Known Variables A, C, and D

    Hi, It seems I've forgotten more of my algebra than I thought. I am putting together a spreadsheet to help a few archers determine how to change their point of aim for up- and downhill shots. I would like to reduce/rearrange the following expression so that A and B are not found on the same...
  29. J

    A very challenging question regarding in basic algebra group theory?

    1.Why Aut(G)=S_G implies G is trivial? I search through the internet and no answer.2.Here is another very difficult conception question which has different answers from my professor and wikipedia: Difference between Symmetry group,automorphism group and Permutation group? From...
  30. KevinMWHM

    Solving Basic Algebra Question 1: x - (-6) = 12

    1. x - (-6) = 12 To simplify, I want to get rid of the (-6). So wouldn't I say 2. x - (-6) +6 = 12 + 6 x = 18? The book I'm using says to add (-6) to both sides but doesn't a neg + neg still equal a neg? I've been flawless to this point, what's confusing me? The books answer 2. x...
  31. S

    How can I break down the steps and solve my basic algebra homework problems?

    I'm so far behind because I've been out of College for so long and I've forgotten Basic Algebra. Can anyone help me break down the steps and solve my homework problems?
  32. T

    Solving for a and b: Fast Method for a^4 + b^4 Calculation

    Homework Statement Given that a-b = 5 and ab = 2, what is the value of a^4 + b^4? Homework Equations The Attempt at a Solution Doing the math I know that a_{1} = \frac{5+\sqrt{33}}{2} a_{2} = \frac{5-\sqrt{33}}{2} b_{1} = \frac{-5+\sqrt{33}}{2} b_{2} = \frac{-5-\sqrt{33}}{2}...
  33. M

    Basic algebra responsible for brain fart

    Homework Statement I'm trying to solve for x in a chemical equilibrium problem (college chem). Once x is found I have no problem finding equilibrium concentrations. What's important is below. Homework Equations 5.10 = [(1+x)/(1-x)]^2 --------> x=.387 (right answer) The Attempt at a...
  34. A

    How Do These Algebraic Expressions Equate in an ODE Problem?

    Homework Statement I'm doing an ODE problem, and I have a set of solutions for it, but I do not understand how \frac{y+1}{y-1} = Cx^2 can equal y = \frac{1+Cx^2}{1-Cx^2} Many Thanks!
  35. E

    What Is the Best Algebra Refresher Book for a Calculus Student?

    I am currently enrolled in Calculus I and am doing fine, the class is very easy as far as calculus concepts go but I struggle with the algebra. It's been 4-5 years since I took algebra so I don't remember a whole lot and really don't want to take the class over. With that said, are there any...
  36. C

    From point A to point B, basic algebra.

    Homework Statement I'm not sure how to get from point A to point B. It seems simple enough, but I'm just not seeing it! Homework Equations point A: \frac{81}{n^4} \ [\frac{n(n+1)}{2}]^2 \ - \ \frac{54}{n^2} \ [\frac{n(n+1)}{2}] point B: \frac{81}{4} \ (1 + \frac{1}{n})^2 \ - \ 27(1 +...
  37. P

    Master Basic Algebra with Knapp's Comprehensive Textbook

    Hi, I wonder if I'm posting my question at a right place, but does anybody know if this is a good textbook for abstract algebra, especially for someone who's taking a "serious" math course for the first time? BASIC ALGEBRA by Anthony W. Knapp...
  38. M

    Trouble with very basic algebra question

    Homework Statement Determine all x in R such that the following hold: 1) (x+4/x-2) < x 2) |x+4/x-2| < x 3) |2x| > |5-2x| Homework Equations We have the triangle inequality, |a + b| \leq |a| + |b|, which also implies the relation ||a| - |b|| \leq |a-b|. Also, relations such...
  39. K

    How to Simplify a Series with Basic Algebra?

    \sum (2^(2n)-(-7)^n)/(11^n) The book has that expression equal to \sum (4/11)^n - \sum (-7/11)^n I'm not seeing how the first part changes to (4/11)^n. Wouldn't it be (2^2+2^n) & not 4^n? Or is there something else I'm missing?
  40. B

    Factoring Equations with Real Roots

    Homework Statement Not sure how to factor this equation: x^4-x^3-x^2+4=0 btw , I do not have a TI 83 calculator
  41. K

    How Do You Separate Complex Equations into Real and Imaginary Parts?

    Homework Statement Write z^3 + 5 z^2 = z + 3i as two real equations Homework Equations z=a+bi? The Attempt at a Solution I've been just playing around with this. I expanded, grouped the real and imaginary parts. I'm really just think I'm groping around desperately in the dark. I think...
  42. B

    Some basic algebra (using Isomorphism Theorems)

    Homework Statement Let G be a group with a normal subgroup N and subgroups K \triangleleft H \leq G. If H/K is nontrivial, prove that at least one of HN/KN and (H\cap N)/(K\cap N) must be nontrivial. Homework Equations The Three (or Four) Isomorphism Theorems. The Attempt at...
  43. K

    Fairly basic algebra question - but it's bugging me now

    Hi, I'm just going through some notes on linear interpolation, but this bit has got me confused - I think it's an easy work through on gradients etc, but my maths seems to be failing me (mature student here so go easy on me :shy: ) Ok here goes (see attached images - not sure about latex...
  44. A

    Solve Abu Kamil's Algebra Puzzle from 9th/10th Century

    "One says that ten is divided into three parts, and if the small one is multiplied by itself and added to the middle one multiplied by itself, it equals the large one multiplied by itself, and when the small is multiplied by the large, it equals the middle multiplied by itself." This is a...
  45. quasar987

    Confusion with very basic algebra

    I'm trying to find the points t in (0,2\pi) such that sint=sin4t. So I use the fact that sinA=sinB <==> A=B+2n\pi (n\in\mathbb{Z}), which yields t=2n\pi/3 (n\in\mathbb{Z}). The only solutions of this in (0,2\pi) are 2\pi/3 and 4\pi/3. However, there are 7 intersection points, says the "indirect...
  46. B

    Simplify Your Limit Problem with Basic Algebra Techniques"

    Okay, basic question. I'm working a limit problem and trying to factor part of my fraction: t3 + 3t2 - 12t + 4 Isn't there a way to combine like terms or something? I feel embarrassed asking this lol.
  47. P

    Simplifying Basic Algebra Equations: An Explanation and Example

    basic algebra question please help :( when combining the two equations Vb-0.5FAC = 10 Hb -0.866FAC = -2 It brings the answer 1.732Vb - Hb = 19.32 can someone plx explain to me how this answer came about
  48. D

    Finding GCF of 3 Terms: 102k^5m^2, 51k^4m, 153k^2m^2

    hey guys, getting back into some basic algebra (so hope you don't mind a real newbie) and was doing a factoring tutorial on the web, and came across this. The work for finding the GCF of three terms is shown below. 102k^5m^2 51k^4m 153k^2m^2 First find the GCF of the coefficients...
  49. K

    How to Solve Basic Algebra Questions: Tips and Tricks

    I have a few nagging questions that are preventing me from solving calculus problems.. Can someone give me a hand? ---------- Question 1 e^xy' = (4x+1)y^2 From the equation above, is it possible to do this: \frac{y'}{y^2} = \frac{4x+1}{e^x} Aren't you supposed to divide one...
  50. N

    Basic Algebra: Showing E = .5(k/a) Without The Conjugate

    Can someone explain to me why E = .5(k/a)(e^2 - 1)/(1 - e^2) = .5(k/a) The conjugate won't work, how do I show this?
Back
Top