Coordinates Definition and 1000 Threads
-
2
Undergrad Cartesian coordinates to Polar coordinates (dx,dy question)
The usual change of variables in this case (mentioned in the title of this topic) is this: ##x = rcos(t)## ##y = rsin(t)## When I rewrite (say my integral) in polar coordinates I have to change ##dxdy## to ##rdrdt## My question is why can't I just compute dx and dy the usual way (the already... -
M
Undergrad Velocity in plane polar coordinates
Hi, I have a problem with the following explanation of velocity in plane polar coordinates. I don't understand why the magnitude of Δer is approximately equal to Δθ. Thanks -
Graduate Momentum operator in curvilinear coordinates
This paper is about momentum operator in curvilinear coordinates. The author says that using \vec p=\frac{\hbar}{i} \vec \nabla is wrong and this form is only limited to Cartesian coordinates. Then he tries to find expressions for momentum operator in curvilinear coordinates. He's starting...- ShayanJ
- Thread
- Coordinates Curvilinear Curvilinear coordinates Momentum Operator
- Replies: 82
- Forum: Quantum Physics
-
W
Two Signs for Rate of Change of Angle in Polar Coordinates
Homework Statement I didn't know if this was considered "advanced" physics, but it's an intermediate classical mechanics course so I'll just post my question here. Basically, if you have a cardioid ##r(\theta)=k(1+\cos(\theta))##, you can show that the ##\dot{\theta}=\frac{v}{\sqrt{2kr}}##...- whoareyou
- Thread
- Angle Change Coordinates Polar Polar coordinates Rate Rate of change
- Replies: 13
- Forum: Advanced Physics Homework Help
-
B
Finding flux through ellipsoid in Cylindrical Coordinates
Homework Statement Using Cylindrical coordinates, find the total flux through the surface of the ellipsoid defined by x2 + y2 + ¼z2 = 1 due to an electric field E = xx + yy + zz (bold denoting vectors | x,y,z being the unit vectors) Calculate ∇⋅E and then confirm the Gauss's Law Homework...- BrianA.
- Thread
- Coordinates Cylindrical Cylindrical coordinates Ellipsoid Flux
- Replies: 3
- Forum: Advanced Physics Homework Help
-
M
Undergrad Finding area in polar coordinates
I've attached the solution to this post. The question is essentially just asking to find the area in one loop for r = cos[3(theta)]. This seems like a fairly simple question (and answer). I've solved and understand the general integration, but I am just a little uncertain on why exactly... -
P
Graduate Double integral in Rectangular coordinates for anything circular
This is the equation for the cone A \sqrt{x^2 + y^2} The double integral \iint A \sqrt{x^2 + y^2} \space dy \space dx \space \space \space\text {From x= -1 to 1 and y=} -\sqrt{1-x^2} \space to \space \sqrt{1-x^2} \text{ is very difficult to evaluate. I've tried polar coordinate substitution...- PaultheRiemann
- Thread
- Circular Coordinates Double integral Integral Rectangular
- Replies: 5
- Forum: Calculus
-
A
Graduate A question of history concerning Rindler Coordinates
Shalom 1. Does anybody know where it is possible to read the original publication of Wolfganng Ridler (May he live long and be blessed) about Rinder coordinates? (acclerated observer in flat spacetime) When was it published? when was the decision to name it after him? 2. Is there any...- Ammah
- Thread
- Coordinates History
- Replies: 7
- Forum: Special and General Relativity
-
C
Separation of Variables Spherical Coordinates
Homework Statement So I'm doing a question from one of my past exams as attached, there are no copy right issues with this document that I know of and have asked my lecturer who wrote the exam and he said I am welcome to upload it. The question is 1)b)iv), my attempt is attached. I end up with...- cooev769
- Thread
- Coordinates Poisson Separation Separation of variables Spherical Spherical coordinates Variables
- Replies: 1
- Forum: Advanced Physics Homework Help
-
M
Area of circle in polar coordinates
Homework Statement r=2cos(theta) I want to find the area using polar integration. Homework Equations area=(1/2)r^2 from 0-pi The Attempt at a Solution When I plug everything in I get 2pi as the answer. I'm in multivariable calculus so this is very frustrating. What am I doing wrong, I don't...- Malabeh
- Thread
- Area Circle Coordinates Polar Polar coordinates
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-

MATLAB [MATLAB] Modeling gravity using polar coordinates Argh
I've been using MATLAB (ode45) to simulate the mechanics of a rocket under the forces of gravity, drag, and internal thrust.y I've recently refactored my simulation to include 2d space, orientation of the rocket, etc. (So I can try to make it orbit, finding optimal ascent profiles, etc)...- ellipsis
- Thread
- Coordinates Gravity Matlab Modeling Polar Polar coordinates
- Replies: 4
- Forum: MATLAB, Maple, Mathematica, LaTeX
-
A
Graduate Transforming Spherical Angles to Cartesian Coordinates for Beam Dynamics
Hello I have this problem - From a generator, I get a compton scattering with the electrons theta and phi angles. where I having the following equations for a particle px = E_particle * sin (theta) * cos (phi); py = E_particle * sin (theta) * sin (phi); pz = E_particle * cos (theta)...- Alkass
- Thread
- Angles Beam Cartesian Cartesian coordinates Coordinates Dynamics Spherical
- Replies: 10
- Forum: High Energy, Nuclear, Particle Physics
-
A
How Do You Prove the Time Derivatives of Polar Unit Vectors?
Homework Statement Prove: $$\frac{d\hat{r}}{dt} = \dot{\phi} \hat{\phi }$$ and $$\frac{d\hat{\phi}}{dt} = -\dot{\phi} \hat{r }$$Homework EquationsThe Attempt at a Solution I solved this for an Analytical Mechanics assignment a month ago, and completely forgot how it goes.. $$\hat{r} ⊥...- A2Airwaves
- Thread
- Analytical mechanics Coordinates Polar Polar coordinates
- Replies: 4
- Forum: Introductory Physics Homework Help
-
S
Find the volume of the region D using spherical coordinates
Homework Statement The problem and its solution are attached as TheProblemAndSolution.jpg. Homework Equations V(D) = ∫∫∫_D ρ^2 sinθ dρ dϕ dθ The Attempt at a Solution How exactly does the solution get cos α = 1/√(3)? Also, when the solution goes from the step with two integrals to the step...- s3a
- Thread
- Coordinates Spherical Spherical coordinates Volume
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
J
Spherical coordinates of Partial Differential Equation
Homework Statement I have a PDE and I need to solve it in spherical domain: $$\frac{\partial F(r,t)}{\partial t}=\alpha \frac{1}{r^2} \frac{\partial}{\partial r} r^2 \frac{\partial F(r,t)}{\partial r} +g(r,t) $$ I have BC's: $$ \frac{\partial F}{\partial dr} = 0, r =0$$ $$ \frac{\partial...- jhartc90
- Thread
- Coordinates Differential Differential equation Partial Partial differential equations Spherical Spherical coordinates
- Replies: 16
- Forum: Engineering and Comp Sci Homework Help
-
S
Curl of Z-unit vector in spherical coordinates
Homework Statement There is a sphere of magnetic material in a uniform magnetic field \vec H_0=H_0\vec a_z, and after some calculations I got the magnetic moment vector \vec M_0=M_0\vec a_z, where M_0 is something that isn't important to my question. I am unsure if this magnetic moment vector...- SalcinNossle
- Thread
- Coordinates Cross product Curl Magnetic fields Spherical Spherical coordinates Vector
- Replies: 3
- Forum: Advanced Physics Homework Help
-

Graduate Light Cone Coordinates Explained
Hi guys, I'm trying to understand light cone coordinates for which I uploaded this picture. The light cone coordinates are given by x^{+}= \frac{1}{\sqrt{2}} (x^{0}+x^{1}) x^{-}= \frac{1}{\sqrt{2}} (x^{0}-x^{1}) Now how should I think of this? I guess the space curves do only life in the space...- JonnyMaddox
- Thread
- Cone Coordinates Light Light cone
- Replies: 1
- Forum: Special and General Relativity
-

Describing the motion of a particle using polar coordinates
1. Problem Consider a particle that feels an angular force only of the form: F_θ = 3mr'θ'. Show that r' = ± (Ar^4 + B)^(1/2), where A and B are constants of integration, determined by the initial conditions. Also, show that if the particle starts with θ' ≠ 0 and r' > 0, it reaches r = ∞ in a...- NATURE.M
- Thread
- Coordinates Motion Particle Polar Polar coordinates
- Replies: 10
- Forum: Introductory Physics Homework Help
-
F
Circular Motion using polar coordinates - Mechanics
Homework Statement A block of mass M is on a frictionless table that has a hole a distance S from the block. The block is attached to a massless string that goes through the hole. A force F is applied to the string and the block is given an angular velocity w0 , with the hole as the origin, so...- fishking2
- Thread
- Circular Circular motion Coordinates Mechanics Motion Polar Polar coordinates
- Replies: 11
- Forum: Introductory Physics Homework Help
-
U
Graduate How do I account for a Jacobian when changing coordinates for two particles?
I am computing matrix elements of a two body quantum-mechanical potential, which take the form V_{k l m n} = \int d^3 r_1 d^3 r_2 e^{-i k \cdot r_1} e^{-i l \cdot r_2} V( | r_1-r_2 | ) e^{i m \cdot r_1} e^{i n \cdot r_2} To do this integral, I make the change of coordinates...- UVCatastrophe
- Thread
- Coordinates Fourier transform Jacobian Two body problem
- Replies: 1
- Forum: Calculus
-
S
Convert this integral from cartesian coordinates to polar coordinates
Homework Statement The problem and its solution are attached as TheProblemAndTheSolution.jpg. If you don't want to view the attached image, the cartesian-coordinate version that the problem wants me to convert to a polar-coordinate version is the following (let "int" = "integral").: int int (1...- s3a
- Thread
- Cartesian Cartesian coordinates Convert Coordinates Integral Polar Polar coordinates
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
H
Graduate Blackbody emission in 2D coordinates
The spectral radiance of a blackbody has units of W·sr-1·m-2·Hz-1. How do I deal with these units if I want to think about a 2D problem of radiation in Cartesian coordinates? I assume that instead of a sphere of emission (which would result in artificial decrease in intensity with the inverse...- Hypatio
- Thread
- 2d Blackbody Coordinate system Coordinates Emission Radiation
- Replies: 3
- Forum: Thermodynamics
-
E
Iterated integral in polar coordinates
Homework Statement Use polar coordinates to find the volume of the solid inside the hemisphere z=sqrt(16-x^2-y^2) and inside the cylinder x^2+y^2-4x=0 Homework Equations z=sqrt(16-x2-y2) x2+y2-4x=0 x=rcos(Θ) y=rsin(Θ) z=√(16-r2) The Attempt at a Solution ∫∫ r√(16-r2) dr dΘ The problem is...- e^(i Pi)+1=0
- Thread
- Coordinates Integral Polar Polar coordinates
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

Line Integral - Stokes theorem
Homework Statement Hello I was given the vector field: \vec A (\vec r) =(−y(x^2+y^2),x(x^2+y^2),xyz) and had to calculate the line integral \oint \vec A \cdot d \vec r over a circle centered at the origin in the xy-plane, with radius R , by using the theorem of Stokes. Another thing, when...- AwesomeTrains
- Thread
- Coordinates Curl operator Integral Line Line integral Stokes Stokes theorem Theorem Vector field
- Replies: 13
- Forum: Calculus and Beyond Homework Help
-

Graduate Which Local Coordinates Are Best Suited for Different Problems and Applications?
In my, er, studies I've encountered descriptions of what I understand to be various ways to go from global to local coordinates. These are: tetrads, Riemann Normal Coordinates and Fermi Normal coordinates. Until now I haven't investigated much further than that, mostly because I've not been...- m4r35n357
- Thread
- Coordinates Local
- Replies: 4
- Forum: Special and General Relativity
-
P
High School What is the Negative of a Polar Coordinate?
Hi, Say I have a variable 'x' which has the polar value 10@-75°, would '-x' be -10@+75° or 10@+75° as I am a touch confused as to which bit I have to invert- Physicist3
- Thread
- Coordinates Negative Polar Polar coordinates
- Replies: 2
- Forum: General Math
-
P
Does the gradiant change when stretching coordinates?
Homework Statement Well, if you have given a gradiant in cartisian coordinate system? what happened to the gradiant if we stretched the coordinates by factor of 2? Homework EquationsThe Attempt at a Solution I think gradiant should be the same as it's the rate of change of some function.- physicsfreak88
- Thread
- Change Coordinates
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
K
Poisson Summation in Heat Equation (Polar Coordinates)
Homework Statement I'm currently trying to follow a derivation done by Shankar in his "Basic Training in Mathematics" textbook. The derivation is on pages 343-344 and it is based on the solution to the two dimensional heat equation in polar coordinates, and I'm not sure how he gets from one...- kamion42
- Thread
- Coordinates Heat Heat equation Laplacian Poisson Polar coordinates Summation
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

MHB Find the coordinates of the expression
Find the coordinates of the expression (cos x + sin x)^3 in the basis {1, sin x, cos x, sin 2x, cos 2x, sin3x, cos3x}. I don't understand where to start since I am dealing with cos and sin now. :confused:- Logan Land
- Thread
- Coordinates Expression
- Replies: 4
- Forum: Linear and Abstract Algebra
-

MHB Find coordinates of f′, f′′, f′′′ in the basis
Consider the polynomial f(x) = x^5 − 5x^4. (a) Find coordinates of f′, f′′, f′′′ in the basis {1, x, x2, x3, x4, x5} I no f ' = 5x^4-20x^3 f " = 20x^3-60x^2 and f "' = 60x^2-120x but from there where to begin? do I make a matrix of like the following? 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0...- Logan Land
- Thread
- Basis Coordinates
- Replies: 20
- Forum: Linear and Abstract Algebra
-
K
Graduate Spherical Coordinates Confusion: Which Set is Correct?
I am accustomed to ##x=rcos(\theta)sin(\phi)## ##y=rsin(\theta)sin(\phi)## ##z=rcos(\phi)## ##-\pi<\theta<\pi##, ##-\pi/2 < \phi < \pi/2## but see some people using these instead ##x=rcos(\theta)cos(\phi)## ##y=rsin(\theta)cos(\phi)## ##z=rsin(\phi)## ##-\pi<\theta<\pi##, ##-\pi/2 < \phi <...- kkz23691
- Thread
- Confusion Coordinates Spherical Spherical coordinates
- Replies: 4
- Forum: Differential Geometry
-
V
Laplace's Equation in Cylindrical Coordinates (Potential)
Homework Statement A hollow cylinder with radius ##a## and height ##L## has its base and sides kept at a null potential and the lid on top kept at a potential ##u_0##. Find ##u(r,\phi,z)##. Homework Equations Laplace's equation in cylindrical coordinates...- V0ODO0CH1LD
- Thread
- Coordinates Cylindrical Cylindrical coordinates Laplace's equation Partial differential equations Potential
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
K
Undergrad Transform Cylindrical coordinates into Cartesian Coordiantes
I've learned that a vector in coordinate system can be expressed as follows: A = axAx+ayAy+azAz. ai, i = x, y, z, are the base vectors. The transformation matrix from cylindrical coordinates to cartesian coordiantes is: Ax cosΦ -sinΦ 0 Ar Ay = sinΦ cosΦ...- kexanie
- Thread
- Calculus Cartesian Coordinates Cylindrical Cylindrical coordinates Linear algebra Transform
- Replies: 3
- Forum: Linear and Abstract Algebra
-
I
Graduate Line integral around a circle, using polar coordinates
Given the force (derived from a potential in planar polar coordinates) F(p,w) = 2p+sin(w)e_p+cos(w)e_w Where e_p and e_w are unit vectors How do I calculate the line integral over a circumference that is defined as: p = 2 0 ≤ w ≤ 2pi Using the definition of a line integral \int_0^{2pi} \... -
J
Graduate Goldstein Mechanics example motion of one particle in polar coordinates
I have a course next semester on Classical Mechanics (mostly Lagrangian problems), for a second time. I'm ok for the theoretical preparation, but I'm trying to work ahead on problems and exercises, which was badly explained and without much of any resources. So, one of the sources to exercise on... -
J
Double integral change of variable polar coordinates question
Homework Statement evaluate the double integral of cosh(6x^2+10y^2) dxdy by making the change of variables x=rcos(theta)/sqrt(3) and y=rsin(theta)/sqrt(5) let D be the region enclosed by the ellipse 3x^2+5y^2=1 and the line x=0 where x>0. Homework EquationsThe Attempt at a Solution first I...- jamesdocherty
- Thread
- Change Coordinates Double integral Integral Polar Polar coordinates Variable
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
R
Solving Laplace Equation in Cylindrical Coordinates - Potential Outside Cylinder
The potential on the side and the bottom of the cylinder is zero, while the top has a potential V_0. We want to find the potential outside the cylinder. Can I use the same boundary conditions as for case of inside cylinder potential? What is different?- ricky123
- Thread
- Coordinates Cylinder Cylindrical Cylindrical coordinates Laplace Laplace equation Outside Potential
- Replies: 3
- Forum: Advanced Physics Homework Help
-
A
Cross Products in Spherical Coordinates: Is A x B True?
Is A x B = | i j k | also true for Spherical Coordinates? | r1 theta1 phi1 | | r2 theta2 phi2 | Or I have to convert them to Cartesian Coordinates and do the cross product and then...- aiaiaial
- Thread
- Coordinates Cross Spherical Spherical coordinates
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
C
Graduate Rindler Coordinates: Signals That Never Arrive
Hi everybody, I know that there are a lot of threads in this forum about Rindler coordinates but none of them have helped me :confused: I'll explain you my problem. First of all, my coordinates (x^0,x) (Cartesian coord., where x^0=ct) are related to the Rindler coordinates (\omega ^0,\omega)...- Cancer
- Thread
- Coordinates Signals
- Replies: 13
- Forum: Special and General Relativity
-
E
Spherical Coordinates Question
Homework Statement I'm feeling a bit ambivalent about my interpretation of spherical coordinates and I'd appreciate it if someone could clarify things for me! In particular, I'd like to know whether or not my derivation of the coordinates is legitimate. Homework Equations Considering...- eyesontheball1
- Thread
- Coordinates Spherical Spherical coordinates
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-

Divergence in cylindrical/spherical coordinates
Homework Statement I'm just having trouble understanding a step in my notes from class.. We're talking about how to derive the divergence in other coordinate systems. Homework Equations So, we are deriving this divergence formula in spherical coordinates \oint \vec{A}\cdot d\vec{A} = \int...- deedsy
- Thread
- Coordinates Divergence Online classes
- Replies: 1
- Forum: Introductory Physics Homework Help
-
M
Graduate Physical Interpretation of Coordinates in GR
What is the relationship between the differentiable manifold that is space-time and the physical space around us? How does one relate the three seemingly Cartesian coordinates around us, those which we can measure out with a ruler, to the coordinates of the Lorentzian manifold? If i say, measure...- MrBillyShears
- Thread
- Coordinates Gr Interpretation Physical
- Replies: 3
- Forum: Special and General Relativity
-
P
Graduate Units for Coordinates - Understanding the Debate
I was reading "Time scales in the context of general relativity" Bernard Guinot, and a few other papers whose names I forget, and was surprised that there was apparently some desire by some physicists to give coordinates units. It seems that the current recommended practice is that...- pervect
- Thread
- Coordinates Units
- Replies: 8
- Forum: Special and General Relativity
-

Mechanics in cartesian coordinates
Homework Statement A cannon shoots a ball at an angle θ above the horizontal ground. (a) Neglecting air resistance, use Newton's second law to find the ball's position as a function of time. (Use axes with x measured horizontally and y vertically.) (b) Let r(t) denote the ball's distance...- Ascendant78
- Thread
- Cartesian Cartesian coordinates Coordinates Mechanics
- Replies: 3
- Forum: Introductory Physics Homework Help
-
M
Polar Coordinates [Finding the velocity]
Homework Statement The projectile A is being tracked by the radar at O. At a given instant, the radar readings are θ = 30degrees, R = 2000m, dR/dt = 200 m/s, and d^2R/dt^2 = 20 m/s^2. Determine the speed of the projectile at that instant. THE ANSWER AT THE BACK IS 299.7m/s [PLEASE SEE...- MrMechanic
- Thread
- Coordinates Polar Polar coordinates Velocity
- Replies: 8
- Forum: Introductory Physics Homework Help
-
A
Curvilinear basis in spherical polar coordinates
Homework Statement As a part of my self study I am trying to find the covariant basis vectors in the spherical polar coordinates. Since I have never done anything like this before I would appreciate if someone could tell me whether I am on the rigth track. Homework Equations...- asdfghhjkl
- Thread
- Basis Coordinates Curvilinear Polar Polar coordinates Spherical
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-

Torque about a point given coordinates in three dimensions
Homework Statement Let \vec{F}=2\hat{i}-3\hat{j} act on an object at point (5,1,3). Find the torque about the point (4,1,0) Homework Equations \tau = \vec F \times \vec r The Attempt at a Solution Please tell me if my procedure is correct. Let the object occupy point A at (5,1,3) and let...- squelch
- Thread
- Coordinates Dimensions Point Torque
- Replies: 9
- Forum: Introductory Physics Homework Help
-
E
MHB Notation for vector coordinates in a given basis
Sorry for a long post. I am looking for a clear and concise way to explain how to compute coordinates when changes of basis or linear operators are involved. I would like to avoid the summation notation as much as possible and use the definition of matrix multiplication only in the beginning...- Evgeny.Makarov
- Thread
- Basis Coordinates Notation Vector
- Replies: 1
- Forum: Linear and Abstract Algebra
-
A
Graduate Derivation of LLG equation in polar coordinates
The torque contribution due to the uniaxial anisotropy is given by the equation below \frac{\Gamma}{l_m K} = (2 \sin\theta \cos\theta)[\sin\phi e_x - \cos\phi e_y] (3) This contribution can be taken in the LLG equation to derive the LLG equation in polar coordinates \frac{\partial...- apervaiz
- Thread
- Coordinates Derivation Polar Polar coordinates
- Replies: 3
- Forum: Atomic and Condensed Matter
-
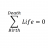
Solving Homework: Polar Coordinates Issue on Volume
Homework Statement My answer seems to differ from the books answer, so I'm wondering where something has gone wrong. Find the volume inside the prism bounded by the planes ##y = x##, ##y = 0##, ##x = \frac{a}{\sqrt{2}}##, ##z = 0## and the cone ##az = h\sqrt{x^2 + y^2}##. Homework...- STEMucator
- Thread
- Coordinates Polar Polar coordinates
- Replies: 9
- Forum: Calculus and Beyond Homework Help