Domain Definition and 704 Threads
-
M
MHB An Artinian integral domain is a field
Hey! :o I want to show that an Artinian integral domain is a field. Let $R$ be an Artinian integral domain and $a\in R$ with $a\neq 0$. Can we take then the sequence $(a)\supseteq (a)^2\supseteq (a^3)\supseteq \dots $ ? (Wondering) Since $R$ is an Artinian integral domain we have that...- mathmari
- Thread
- Domain Field Integral
- Replies: 4
- Forum: Linear and Abstract Algebra
-

Solve Laplace equation on rectangle domain
Homework Statement I'm having issues with a Laplace problem. actually, I have two different boundary problems which I don't know how to solve analytically. I couldn't find anything on this situations and if anybody could point me in the right direction it would be fantastic. It's just Laplace's...- Dor
- Thread
- Boundary conditions Domain Laplace Laplace equation Rectangle Seperation of variables
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
A
Finding the Domain of a Trigonometric Function
Homework Statement Find the domain of this function and check with your graphing calculator: f(x)=(1+cosx)/(1-cos2x) Homework EquationsThe Attempt at a Solution i get to (1+cosx)/(1+cosx)(1-cosx) which is factored. so then setting each one to zero one at a time i figure out that cosx = -1 and...- Astraithious
- Thread
- Domain Function Functions Trig Trig functions Trig identities
- Replies: 6
- Forum: Precalculus Mathematics Homework Help
-
S
MHB Math Notation: How to explicitly specify the domain of a function symbolically?
How can I specify the domain of a function symbolically? Assume I have a very simple linear function. $f(x)=2x$ If I want to say that the domain of this function is all the real numbers, how would I write this with symbols? Do I need to use set-builder notation? What would the set-builder...- samir
- Thread
- Domain Function Notation
- Replies: 11
- Forum: General Math
-
S
Is xy>0 Sufficient to Determine the Domain of f(x, y) = xy√(x²+y)?
Homework Statement Find the domain of the function: f(x,y) = xy*√(x2+y) Homework Equations The domain is the set of all input values for which the function is defined. The Attempt at a Solution D = {(x,y): xy>0} I plugged the function into Wolfram and it gave the result: D = {(x,y): x2+y ≥...- says
- Thread
- Domain Function
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
S
MHB Modifying values to lie within existence domain
Given three parameters: $$a= \frac{(k-3)^2 \sqrt{v}}{s}, \ \ b = \frac{v}{s}(w-10s), \ \ c = s \sqrt{v}.$$ which exact values I know (that is, I know $v,s,k$ and $w$ exactly). I need to guarantee that $a<0$ (this is always satisfied in my calculations!) and $$0<b<1.08148a^2$$ For instance, if... -
S
Find the domain of the function
Homework Statement Find domain of f(x, y) = ln ((x2+2x+y2) / (x2−2x+y2)) Homework EquationsThe Attempt at a Solution Because the function is a natural ln, the restriction on the function is that everything inside the brackets has to >0, otherwise the function is undefined. I worked on the...- says
- Thread
- Domain Function
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
M
Help -- Time Domain Power, Volt-Amperes in lagging circuit
Please find attached a spreadsheet trying to plot an inductive/resistive circuit in the time domain and show instantaneous power and Volt Amperes. Logic tells me power can not go negative, but I am not sure my power plot is correct. Can someone please review the spreadsheet and chart to tell me...- mdaugird
- Thread
- Circuit Domain Power Time Time domain
- Replies: 18
- Forum: Electrical Engineering
-
C
Find and Sketch the Domain of a Function
Homework Statement ƒ(x,y) = √y + √[25-x2-y2] Homework Equations Quadratic The Attempt at a Solution The expression for f(x,y) is defined as long as x2 + y2 ≥ 25 and y ≥ 0 because of the square roots we can't have negative numbers. {(x,y) ∈ ℝ2 : y ≥ 0 and x2 + y2 ≥ 25} I'm not sure how I'd...- cosmos42
- Thread
- Calculus Calculus 3 Domain Function Sketch
- Replies: 1
- Forum: Precalculus Mathematics Homework Help
-

Integral Domain, r^2 = r proof that r = 0 or 1
Homework Statement Let r be an element of an integral domain R such that r^2 = r. Show that either r = 0_R or 1_R Homework Equations integral domain means no zero divisors. The Attempt at a Solution This is fundamental as 0 and 1 solve r^2 = r and are the only solutions. However, I'm not...- RJLiberator
- Thread
- Domain Integral Proof
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
J
Run-time error M6201: math -log: DOMAIN error
Hi all, I am facing the problem while executing my fortran (77) program. please help me how to fix it. As I understood, the error means that the domain of log function has included zero values or negative values...But I could not understand...In my case... there are no zero or negative...- js6201
- Thread
- Domain Error Log
- Replies: 1
- Forum: Engineering and Comp Sci Homework Help
-
N
D'Alembert solution of wave equation on semi infinite domain
Homework Statement Wave equation: ytt=yxx Initial conditions: Y(x,0) =f(x) = x (0 ≤ x < 1) 2.5(5-x) (1 ≤ x < 3) 0 (Otherwise) and yt(x,0) = 0 Boundary condition: y(0,t) =0 Semi infinite domain: 0 ≤ x < infinity Homework Equations d'Alembert solution...- Name15
- Thread
- D'alembert Domain Infinite Pde Wave Wave equation
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-
M
MHB Finding the Domain of a Function
How do you find the Domain of \sqrt{(x^2 + 4)/(x^2 - 4)} ?- megacat8921
- Thread
- Domain Function
- Replies: 3
- Forum: General Math
-

Local max and min (including a domain)
I have this function: f(x) = √3x + 2Cos(x) I have to find the local maxima and minima,where -π ∠ or equal to x ∠ or equal to 2π. 1: Differentiate the function given. f'(x) = 3/(2√x) -2Sin(x) 2: Find where f'(x) is undefined or = 0 to get critical points. 3: Find f''(x) [The second...- King_Silver
- Thread
- Domain Local Max
- Replies: 17
- Forum: Calculus
-

What Are the Implications of Domain Wall Problems in L=kρσ Interactions?
So I have learned that an interaction term in a Lagrangian like: L= kρσ can result in "domain wall" problems between the fields ρ and σ. I imagine this means that it can result in particles spontaneously changing mass, spin, or some other property, violating conservation laws. Is that why this...- DuckAmuck
- Thread
- Domain Wall
- Replies: 1
- Forum: Beyond the Standard Models
-
T
Optimizing Across Noisy Domain
Are there any established methods for optimizing across a 2D surface with noise? I am trying to find the maximum across a 2D surface, but the surface is extremely noisy. Ideally, I would numerically optimize a function without resorting to computing the entire surface, filtering the surface...- tangodirt
- Thread
- Domain
- Replies: 5
- Forum: General Math
-

How does ifft(fft(x)) form the correct bijection with domain?
I think my question is more appropriate here than in the computation section. My question is: (In the context of inverse fast-fourier transforms and fast-fourier transforms) Knowing ifft(fft(x)=x might be trivial as it is almost a definition; associating it with a domain ##t## is perfectly...- davidbenari
- Thread
- Bijection Domain Form
- Replies: 1
- Forum: General Math
-

Sketching Transfer function in time domain
Homework Statement $$ y(s) = \frac {s}{(s+1)(2s+1)} u(s) $$ Where ##u(s)## is the step function ##\frac {1}{s}## Find the output at t=0 and t= infinity Homework EquationsThe Attempt at a Solution My question is kind of basic, so I know the final and initial value theorem $$ \lim_{s \to 0}...- gfd43tg
- Thread
- Domain Function Time Time domain Transfer function
- Replies: 2
- Forum: Engineering and Comp Sci Homework Help
-
Y
Integration in Frequency Domain
How to integrate $$\int_{-0.5}^{0.5} {\bigg({\frac{1}{4-2e^{-j2{\pi}f}}}\bigg)}^2 df$$- yukari1310
- Thread
- Domain Frequency Frequency domain Integration
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
S
MHB Given a range value, find the correspoding domain value
Here is the problem: If -1 is a range value for the function f(x) = -6x + 11, find the domain value. thank you for your help- sharkman1
- Thread
- Domain Range Value
- Replies: 3
- Forum: General Math
-
C
Finding solution of equation in complex domain?
(1+a)n = (1-a)n I tried following: (1+a)n = (1-a)n [(1+a)/(1-a)]n=1 but what can i do next?- cdummie
- Thread
- Complex Domain
- Replies: 4
- Forum: General Math
-

Domain and range of a function of several variables
Homework Statement Find the domain and range of the following function: f(x, y) = ln(x+y) Homework EquationsThe Attempt at a Solution I know that the natural log ln(x) is only defined when x>0, so does that mean that ln(x+y) is only defined when x+y>0? Also, would the range just be all positive...- yango_17
- Thread
- Domain domain and range Function Range Variables
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-

A path which its domain is a general compact set.
How is a general path called instead of being a continuous function from an interval to some topological space, where we replace the domain from an interval to a compact set, is there a name for such a function? Perhaps I should add that the compact set is also convex.- MathematicalPhysicist
- Thread
- Compact Domain General Path Set
- Replies: 6
- Forum: Topology and Analysis
-
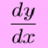
Finding domain of function (need an explanation for 2 Qs)
i need help with finding the domain for a function where there is a square root , here is the picture of such questions : http://imgur.com/YcqadOe please see the picture, there are two questions in it, 35 and 37 let's start with question 35, this is how i try to solve it : x^2 - 5x > 0 x...- iwantcalculus
- Thread
- Domain Explanation Function
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

How do I solve this multiple integral in the given domain?
Homework Statement Hi, I have a problem with the following exercise. Let C={(x,y,z)∈ℝ3 : x2+y2+z2≤1, z≥√(3x2+8y2)} be a subset of ℝ3. Calculate ∫∫∫C z dxdydz.Homework Equations Spherical coordinates, given by x=ρsinΦcosθ, y=ρsinΦsinθ, z=ρcosΦ, and cylindrical coordinates which are x=ρcosα...- Aner
- Thread
- Domain Integral Multiple
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
K
What is a frequency domain and s domain?
What is a frequency domain and how can we understand the same in practical world? How is it related to complex plain sight domain?- KittuTarun
- Thread
- Domain Frequency Frequency domain
- Replies: 1
- Forum: General Math
-
B
MHB Finding Domain of f(x)=\frac{1}{x^{2}-x-6}
I'm supposed to find the domain of this function, I know I'm supposed to set the denominator equal to 0 but I don't know what to do after that, please help! $$f(x)=\frac{1}{x^{2}-x-6}$$ I can't figure out how to make this look like a real fraction but it's supposed to be 1 over x squared minus...- badatmath
- Thread
- Domain
- Replies: 5
- Forum: General Math
-
P
Is the Domain of an Antiderivative Always a Subset?
Isn't the domain of the derivative of a function a subset of the domain of the function itself? Does this mean that the domain of an integrand is always a subset of the corresponding indefinite integral?- PFuser1232
- Thread
- Antiderivative Domain
- Replies: 2
- Forum: Calculus
-
K
MHB Is {0} Considered the Smallest Integral Domain?
What is the smallest (most trivial) integral domain? {0,1} is an integral domain but is {0} an integral domain with unity = 0 and zero = 0? If {0} is not an integral domain then why not?- Kiwi1
- Thread
- Domain Integral
- Replies: 1
- Forum: Linear and Abstract Algebra
-
M
How do I calculate an area of joint uniform distribution with domain
This technically isn't a coursework or homework problem: I have a uniform Joint density function for the lifetimes of two components, let's call them T1 and T2. They have a uniform joint density function, both are positive it follows, and the region is 0<t1<t2<L and L is some positive constant...- mattclgn
- Thread
- Area Distribution Domain Joint Uniform Uniform distribution
- Replies: 3
- Forum: Set Theory, Logic, Probability, Statistics
-

MHB How Do GCDs Coincide in Principal Ideals According to Rotman's Proposition 3.41?
I am reading Joseph J.Rotman's book, A First Course in Abstract Algebra. I am currently focused on Section 3. Polynomials I need help with the a statement of Rotman's concerning the definition of a gcd in a general domain ... the definition The relevant section of Rotman's text reads as...- Math Amateur
- Thread
- Domain
- Replies: 1
- Forum: Linear and Abstract Algebra
-
E
Phase shift in frequency domain
Hello, I'using Matlab to simulate phase shift in frequency domain (FD). I have got real and imaginary parts of the signal after FFT. I'd like to use phase shift in FD. This works: Y=fft(y); YY=Y.exp(-i*2*pi*nk/N*samples_delay); result=ifft(YY); But in my DSP I can't use the formula above and...- Eng_Pat
- Thread
- Domain Dsp Fft Frequency Frequency domain Matlab Phase Phase shift Shift
- Replies: 3
- Forum: Electromagnetism
-

What is the Domain of l/g Without first calculating (l/g)(x)
Homework Statement Write down Dl/g without first calculating (l/g)(x) Homework Equations g(x)=-(1/2)x-3 l(x)=√(2-x)-3 The Attempt at a Solution g(x)=-(1/2)x-3 Dg = {x∈ℝ} l(x)=√(2-x)-3 Dl = {x∈ℝ:x≤2} Dg/l = {x∈ℝ:x≤2}- Jaco Viljoen
- Thread
- Domain
- Replies: 9
- Forum: Precalculus Mathematics Homework Help
-
F
Marginal stabilty in s domain
I'm trying to get a better understanding of marginal stability and the s domain in general. According to my textbook, a system that is marginally stable has poles that are conjugates of each other on the jω axis, and their magnitude are the resonant frequency for which if a sinusoid of that...- FrankJ777
- Thread
- Domain Marginal
- Replies: 1
- Forum: Other Physics Topics
-
R
How frequency domain topic should be taught in the academic course?
This is a soft question but I think it's a real fact.The Frequency domain has made revolution in the field of Mathematics,Physics,Digital Signal and image Processing etc. Some of concepts which are very difficult to analyse in spatial or time domain can be very easily understood in the frequency...- ramdas
- Thread
- Academic Course Domain Fourier Frequency Frequency domain Topic Transformation
- Replies: 4
- Forum: STEM Educators and Teaching
-
B
MHB What is the Solution to $4\sin(x)+3\cos(x)\geq0$ in Terms of Domain and Range?
I need explanation- bahadeen
- Thread
- Domain domain and range Range
- Replies: 2
- Forum: General Math
-

Domain and range of composite functions?
hey! How do you work out the domain and range of fg(x), do you work out what range of g(x) will fit the domain of f(x)? I have no clue. Thanks- CAH
- Thread
- Composite Domain domain and range Functions Range
- Replies: 4
- Forum: General Math
-
T
Domain and range of multivariable functions
Homework Statement Specify the domain and range of f(x, y) = arccos(y − x2). Indicate whether the domain is (i) open or closed, and (ii) bounded or unbounded. Give a clear reason in each case.Homework EquationsThe Attempt at a Solution y-x2 >= -1 y >= x2 -1 y-x2 <= 1 y <= x2 +1 I sketched it...- TheRedDevil18
- Thread
- Domain domain and range Functions Multivariable Range
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
K
MHB Showing a simple function is continuous on a restricted domain
**Motivation:** I am studying for an exam over Chapters $1-3$ of *Real Analysis* by Royden and Fitzpatrick, 4th edition. I am stuck on understanding some of Proposition $11$, which I have reproduced below: **Proposition 11:** Let $f$ be a simple function defined on $E.$ Then for each...- kalish1
- Thread
- Continuous Domain Function
- Replies: 1
- Forum: Topology and Analysis
-

Domain and how it relates to a Level Curve
Homework Statement Find the domain of the function f(x,y) = 1/sqrt(x^2-y). Sketch the level curves f=1, f=1/2, f=1/3. Homework EquationsThe Attempt at a Solution Domain is rather simple to find: x^2>y AND x^2-y cannot equal 0. Level curves are also simple to find. They are simply parabolas...- RJLiberator
- Thread
- A level Curve Domain
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-

Convert the domain of the Tan function to interval notation?
Homework Statement Hey guys. So basically I'm doing some Calc I homework and I'm working on the domain of this function: g(x) = √tan(2x+π) Homework Equations Now to determine the domain, I know that the function under the root cannot be negative. The Attempt at a Solution So after...- Tsubaki
- Thread
- Convert Domain Function Interval Notation Tan
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

What is the domain of ascsin(x+y)
Hey Try to figure out the way to find domain of the function ascsin (x+y) without using the formula can someone give the clue how I should start ? Always confuse about inverse of trigonometry function. Thanks in advance.- Mahathepp
- Thread
- Domain
- Replies: 4
- Forum: Precalculus Mathematics Homework Help
-
F
MHB How to find domain of function in implicit form
What is the domain of $$y^2-2y=x^2-x-1$$? I don't know how to find it for implicit functions.- find_the_fun
- Thread
- Domain Form Function Implicit
- Replies: 6
- Forum: General Math
-
S
Selection of domain and codomain for wave function
A wave function is a function in a Hilbert space of functions. When representing a physical sytem, what are the conventions for defining the domain and codomain of the wave function? For example, is the domain always the scalar variable representing time? Is the codomain a set of finite...- Stephen Tashi
- Thread
- Domain Function Wave Wave function
- Replies: 17
- Forum: Quantum Physics
-

Every field is an integral domain?
Okay, so if r,s are elements of R and rs = 0 then either r or s has to equal zero. I'm just confused because it seems that if rs = 0 then we can show that both r and s must be zero... I don't know what I'm doing wrong.. rs = 0 r^-1(rs) = r^-1(0) = 0 1s = 0 s = 0 and then: rs = 0 r(ss^-1) =...- PsychonautQQ
- Thread
- Domain Field Integral
- Replies: 2
- Forum: Linear and Abstract Algebra
-
R
Why the transfer function is represented in S Domain?
Hi all, I would like to know why the Transfre function of the system is represented in S Domain instead of doing all the math in time domain itself. I studied a course on control systems and i wonder why s- domain is taken instead of other domains like Z- domain and others. Please refer belwo...- Raj
- Thread
- Control systems Domain Function Transfer function
- Replies: 2
- Forum: Other Physics Topics
-
B
MHB Where Does the Convolution Theorem Come From?
Hi Folks, I have an article which explains the modulation of 2 signals given by X_1(f) e^{-j 2 \pi f t_i} and X_2(f) e^{-j 2 \pi f t_i} The only difference between the 2 signals is a time delay, however i don't see a phase difference in either expression It states the convolution of these...- bugatti79
- Thread
- Domain Noise Signal
- Replies: 11
- Forum: General Math
-

MHB Finding Domain & Range of $$y=\sqrt{x^2+y^2}$$
I was thinking about a function whose domain and range are absolutely one point , then I'm stuck in finding the domain and range of the following function .. could anyone help $$y=\sqrt{x^2+y^2}$$- Maged Saeed
- Thread
- Domain domain and range Range
- Replies: 8
- Forum: General Math
-

MHB Is $C[x,y,z]/<y-x^2,z-x^3>$ an Integral Domain?
Hi! (Smile) Can I justify like that, that $C[x,y,z]/<y-x^2,z-x^3>$ is an integral domain? We show that $ker(\phi)=<y-x^2,z-x^3>$. From the theorem of isomorphism, we have that $C[x,y,z]/<y-x^2,z-x^3> \cong im(\phi)$ $im(\phi)$ is a subring of $\mathbb{C}[x]$ $\mathbb{C}[x]$ is an...- evinda
- Thread
- Domain Integral
- Replies: 1
- Forum: Linear and Abstract Algebra
-
A
Prime Ideal & Noetherian Integral Domain
I am reading a graduate-level Abstract Algebra lemma on noetherian integral domain, I am bring it up here hoping for pointers. The original passage is in one big-fat paragraph but I broke it down here for your easy reading. Let me know if I forget to include any underlying lemmas, thank you for...- A.Magnus
- Thread
- Abstract algebra Domain Integral Prime
- Replies: 17
- Forum: Linear and Abstract Algebra