What is Integral: Definition and 1000 Discussions

In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with differentiation, integration is a fundamental, essential operation of calculus, and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others.
The integrals enumerated here are those termed definite integrals, which can be interpreted formally as the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Conventionally, areas above the horizontal axis of the plane are positive while areas below are negative. Integrals also refer to the concept of an antiderivative, a function whose derivative is the given function. In this case, they are called indefinite integrals. The fundamental theorem of calculus relates definite integrals with differentiation and provides a method to compute the definite integral of a function when its antiderivative is known.
Although methods of calculating areas and volumes dated from ancient Greek mathematics, the principles of integration were formulated independently by Isaac Newton and Gottfried Wilhelm Leibniz in the late 17th century, who thought of the area under a curve as an infinite sum of rectangles of infinitesimal width. Bernhard Riemann later gave a rigorous definition of integrals, which is based on a limiting procedure that approximates the area of a curvilinear region by breaking the region into thin vertical slabs.
Integrals may be generalized depending on the type of the function as well as the domain over which the integration is performed. For example, a line integral is defined for functions of two or more variables, and the interval of integration is replaced by a curve connecting the two endpoints of the interval. In a surface integral, the curve is replaced by a piece of a surface in three-dimensional space.

View More On Wikipedia.org
Recent contents Top users
  1. E

    Why is the integral of a(x) different from the integral of a(t)?

    Hello! First time poster, please treat me well! :wink: I've already solved the problem below on my second attempt with the help of kinetic energy but I want to know why my first attempt gives a wrong answer. 1. Homework Statement A force in the +x-direction with magnitude F(x) = 18.0 N -...
  2. Math Amateur

    MHB Understanding Irreducible Elements in Integral Domains - Peter's Questions

    Joseph A. Gallian, in his book, "Contemporary Abstract Algebra" (Fifth Edition) defines an irreducible element in a domain as follows ... (he also defines associates and primes but I'm focused on irreducibles) ... I am trying to get a good sense of this definition ... My questions are as...
  3. Math Amateur

    I Definition of an irreducible element in an integral domain

    Joseph A. Gallian, in his book, "Contemporary Abstract Algebra" (Fifth Edition) defines an irreducible element in a domain as follows ... (he also defines associates and primes but I'm focused on irreducibles) ... I am trying to get a good sense of this definition ... My questions are as...
  4. F

    A On the equivalence of operator vs path integral in QFT

    I have read many textbooks and googled google times for a clear explanation, but I could not find one. How does raising and lowering -annihilation/ creation-(is that energy or particle number?) translate to transition probabilities of path integral.
  5. P

    A Closed form for series over Exponential Integral

    Is there a closed form for the constant given by: $$\sum_{n=2}^\infty \frac{Ei(-(n-1)\log(2))}{n}$$ (Where Ei is the exponential integral)? Could we generalize it for: $$I(k)=\sum_{n=2}^\infty \frac{Ei(-(n-1)\log(k))}{n}$$ ? My try: As it is given that k will be a positive integer, I have...
  6. D

    A How to Solve the Fourier Integral in Eq. (27) Involving Position Vectors?

    Where , rho 1 and rho 2 are two dimensional position vectors and K is a two dimensional vector in the Fourier domain. I encountered the above Eq. (27) in an article and the author claimed that after integration the right hand side gives the following result: I tried to solve this integral but...
  7. X

    Surface Integral of Outward Normal Vector over a Spherical Surface

    Homework Statement Let n be the unit outward normal of a spherical surface of Radius R, let the surface of the sphere be denoted by S. Evalute Surface integral of nndS Homework EquationsThe Attempt at a Solution I have evaluated the surface integral of ndS and found it to be 0. but am not...
  8. Oedipus

    I Closed form solution for this integral

    After series of algebraic simplifications, I ended up with the following integral: ##\int_0^\infty \exp(-Kx) \arctan(x) dx ## As far as I searched, there is no closed form solution for the integral. But, K is my design variable that I need to optimize later. To do this, I need to take K out of...
  9. J

    I Multi-dimensional Integral by Change of Variables

    Hi All, $$\int{\exp((x_2-x_1)^2+k_1x_1+k_2x_2)dx_1dx_2}$$ I can perform the integration of the integral above easily by changing the variable $$u=x_2+x_1\\ v=x_2-x_1$$ Of course first computing the Jacobian, and integrating over ##u## and ##v## I am wondering how you perform the change of...
  10. Mr Davis 97

    I Integrating a Complex Integral using Substitution and Simplification

    I am trying to evaluate the integral ##\displaystyle \int \frac{x}{1+\cos^2x}dx##. I have started by multiplying both the numerator and the denominator by ##\frac{\sin^2x}{\cos^4x}##, to get ##\displaystyle \int \frac{x\frac{\sin^2x}{\cos^4x}}{1+\tan^2x}dx##, and the denominator simplifies to...
  11. Math Henry

    Differentiation question

    Homework Statement [/B] Summarizing: two civilizations hate each other, one of the civilizations throws a curse at the second. The second civilization succumbs to chaos and has a change in Population each week of ΔP= -√P. That is: Pn = Pn-1-√Pn-1 Homework Equations [/B] Considering that the...
  12. Isaac0427

    B Summation vs Integral for Wavefunction Superposition

    When taking the superposition of wavefunctions with definite values of any observable (I'll just use momentum, but I am assuming it would work for any variable), I have seen the integral be used: ##\psi = \int_{-\infty}^{\infty}\phi(k)e^{ikx}dk## and the sum be used: ##\psi =...
  13. P

    I Solve Challenging Integral with Proven Techniques | x>1 Integer Solution

    Hello. I am having a lot of trouble trying to solve/analyse this integral: $$\displaystyle \int_2^\infty \frac{x+y}{(y)(y^2-1)(\ln(x+y))} dy$$ I have tried everything with no result; it seems impossible for me to work with that natural logarithn. I have also tried to compute it, as it...
  14. J

    How can I find this surface integral in cylindrical coordina

    Homework Statement A vector field $\vec F$ is defined in cylindrical polar coordinates $\rho , \theta , z$ by $\vec F = F_0(\frac{xcos (\lambda z)}{a}\hat i \ + \frac{ycos(\lambda z)}{a}\hat j \ + sin(\lambda z)\hat k) \ \equiv \frac{F_0 \rho}{a}cos(\lambda z)\hat \rho \ + F_0sin(\lambda...
  15. D

    Calculus Calculus of variation textbook 'not under a single integral'

    I have to find functions that maximise certain criterea. The problem can however not be put "under a single integral", for example I've to find ##f(t)##, ##g(t)## that maximise: ## \int_0^{t_e}f(t)^2dt\int_0^{t_e}g(t)^2dt - (\int_0^{t_e}f(t)g(t)dt)^2 ## With ## -1 \leq f(t)\leq1## and ## -1...
  16. TheSodesa

    Number of subdivisions in a Riemann integral (DFT)

    Homework Statement This is a combination of two questions, one being the continuation of the other 3) Calculate the DFT of the sequence of measurements \begin{equation*} \{ g \}_{k=0}^{5} = \{ 1,0,4,-1,0,0 \} \end{equation*} 4a) Draw the DFT calculated in question 3 on the complex plane. 4b)...
  17. K

    A Integral of squared univariate PDF

    Hi all, I was trying to find an answer, but couldn't, what is the integral of the squared probability density function? It doesn't seem to be equal to the square of cumulative distribution function, but how to tackle it? ∫(f(x))2dx = ? Can we transform it into, say, ∫f(x)dF(x)? and then...
  18. ShayanJ

    A Path integral formula for a state with non-trivial time dependency

    Consider a system with a time-dependent Hamiltonian. We know that the evolution of the state of this system, is given by ## \displaystyle |\Psi(t_1)\rangle=T \exp\left( -i \int_{t_0}^{t_1} dt H(t) \right) |\Psi(t_0)\rangle ##. Do you think you can prove that the path integral formula for the...
  19. N

    MHB Integral: Solving the Difficult One

    Consider the following: \int \left(\frac{x-1}{x+1}\right)^4\,dx I am unable to solve this.
  20. binbagsss

    Integral quick q , integrate ((1-x)/(1+x))^1/2

    Homework Statement How do I go about integrating ##(\frac{1-x}{1+x})^{\frac{1}{2}} ##? Homework Equations above The Attempt at a Solution im not really sure. could integrate by partial fractions if it was to the power of ##1##, only thing i can think of thanks in advance
  21. grandpa2390

    Why does this integral cut off the z component?

    Homework Statement Please don't make me post the entire question. If so, can I take a picture of the example in my textbook? I am looking at an example in my textbook where we are to check Stoke's theorem After doing the cross-product of del cross v I get (4z^2-2x)[x hat] + (2z^2)[z hat]...
  22. O

    A The meaning of an integral of a one-form

    So I understand that the integral of a differential form ω over the boundary of some orientable manifold Ω is equal to the integral of its exterior derivative dω over the whole of Ω. And I understand that one can pull back the integral of a 1-form over a line to the line integral between the...
  23. T

    Integrating with respect to area? Past paper question

    This isn't exactly homework or coursework, it is a past paper question that I cannot find a solution to (my university doesn't like releasing answers for some reason unknown to me). The question is attached as an image (edit: the image displays while editing but not in the post, so I'll try to...
  24. R

    MHB Surface Integral of $F$ Over Region V

    Let V be the region bounded by the hemisphere z=1-sqrt(1-x^2-y^2) and the plane z=1, and let S be the surface enclosing V. consider the vector field $F= x(z-1)\hat{\imath}+y(z-1)\hat{\jmath}-xy\hat{k}$.
  25. R

    MHB Calculate $\int sze^z dS$ on Unit Sphere

    calculate $\displaystyle \int sze^z dS$ where S is the protion of the unit sphere centered at the origin such that x,y <0, z>0.
  26. kolleamm

    B Difference between integral and a function

    Online it says that the integral is the opposite of the derivative. So x^2 is the integral of 2x. So if f(x) = x^2 , does that mean that the integral is just the function itself? Basically whatever f(x) equals? Thanks in advance
  27. binbagsss

    Inequality quick question context cauchy fresnel integral

    Homework Statement please see attached, I am stuck on the second inequality. Homework Equations attached The Attempt at a Solution I have no idea where the ##2/\pi## has come from, I'm guessing it is a bound on ##sin \theta ## for ##\theta## between ##\pi/4## and ##0## ? I know ##sin...
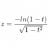
  28. substitute materials

    I Path integral implies superluminal motion?

    In the path integral formalism, where we treat a photon as if it takes every possible path, aren't the possible paths limited by the speed of light? If we were to perform the double slit experiment, and shield the detector after a specified time frame to limit the time for a photon to make the...
  29. I

    Mathematica Numerical solution of integral equation with parameters

    Hello! Could you tell me about how to take the next numerical calculation in mathematica? (perhaps there are special packages). I have an expression (in reality slightly more complex): ## V=x^2 + \int_a^b x \sqrt{x^2-m^2} \left(\text Log \left(e^{-\left(\beta...
  30. Anne Leite

    How to Convert Maxwell's Equations into Integral Form

    Homework Statement I'd like to know how to convert Maxwell's Equations from Differencial form to Integral form. Homework Equations Gauss' Law Gauss' Law for Magnetism Faraday's Law The Ampere-Maxwell Law The Attempt at a Solution Convert using properties of vector analysis (as Divergence and...
  31. A

    MHB What is the Intuition Behind Integral Over in Commutative Algebra?

    Could somebody write me the intuition behind the concept of "Integral Over"? Please do not write me its formal definition, I can easily get it from textbook. What I am also looking for is its motivation behind it. Please give me also examples. For your convenience, the formal definition...
  32. Alettix

    Antiderivative of 1/x: ln(x) or ln(|x|)?

    Homework Statement Calculate the integral: ## \int_{a}^{b} \frac{1}{x} dx ## Homework Equations - The Attempt at a Solution In high school we learned that: ## \int_{a}^{b} \frac{1}{x} dx = ln(|x|) + C ## because the logarithm of a negative number is undefined. However, in my current maths...
  33. Rectifier

    Is There a Constant Lower Bound for the Integral Test of Convergence?

    The problem I am trying to show that the following integral is convergent $$ \int^{\infty}_{2} \frac{1}{\sqrt{x^3-1}} \ dx $$The attempt ## x^3 - 1 \approx x^3 ## for ##x \rightarrow \infty##. Since ## x^3 -1 < x^3 ## there is this relation: ##\frac{1}{\sqrt{x^3-1}} > \frac{1}{\sqrt{x^3}}##...
  34. Rectifier

    Primitive function - smart substitution

    The problem $$ \int \frac{x}{\sqrt{x^2+2x+10}} \ dx $$ The attempt ## \int \frac{x}{\sqrt{x^2+2x+10}} \ dx = \int \frac{x}{\sqrt{(x+1)^2+9}} \ dx## Is there any smart substitution I can make here to make this a bit easier to solve?
  35. Rectifier

    Solving Integral Equations: Find x from 1-x+ ∫^x_1 (sin t/t) dt

    The problem I want to find ##x## which solves ## 1-x+ \int^x_1 \frac{\sin t}{t} \ dt = 0 ## The attempt ##\int^x_1 \frac{\sin t}{t} \ dt = x -1 ## I see that the answer is ##x=1## but I want to be able to calculate it mechanically in case if I get similar problem with other elements. Any...
  36. Rectifier

    Integral Inequality: Prove x-1 > Int(sin(t)/t) for x>1

    The problem Show that ## 1-x+ \int^x_1 \frac{\sin t}{t} \ dt < 0## for ## x > 1 ## The attempt I rewrite the integral as ##\int^x_1 \frac{\sin t}{t} \ dt < x-1 ## This is about where I get. Can someone give any suggestions on how to continue from here?
  37. A

    I Integral of the momentum (with respect to time)

    Hi everybody ! Can anyone help me with this problem: Which is the (indefinite) integral with respect to time of the momentum of a particle of rest mass ##m_0##? ##\int \dfrac{m_0\;\mathbf{v}}{{\sqrt{1-\dfrac{\mathbf{v}\cdot\mathbf{v}}{c^2}}}}\;dt## where ##m_0## is invariant with respect to...
  38. Rectifier

    Understanding the Riemann Sum - Integral Connection

    The problem I want to calculate $$\sum^n_{k=1} \frac{4}{1+ \left(\frac{k}{n} \right)^2} \cdot \frac{1}{n}$$ when ##n \rightarrow \infty## The attempt ## \sum^n_{k=1} \underbrace{f(\epsilon)}_{height} \underbrace{(x_k-x_{k-1})}_{width} \rightarrow \int^b_a f(x) \ dx ##, when ##n \rightarrow...
  39. Rectifier

    Efficient Integration of Step Function with Variable Denominator

    The problem I want to calculate ## \int^6_{-6} \frac{g(x)}{2+g(x)} \ dx ## for the step function below.The attempt I started with rewriting the function as with the help of long-division ## \int^6_{-6} \frac{g(x)}{2+g(x)} \ dx = \int^6_{-6} 1 \ dx - 2\int^6_{-6} \frac{1}{g(x)+2} \ dx## I know...
  40. P

    MHB What is the value of the triple integral for the given solid and region?

    Evaluate the integral \iiint\limits_{ydV}, where V is the solid lying below the plane x+y+z =8 and above the region in the x-y plane bounded by the curves y=1, x=0 and x=\sqrt{y}.
  41. mamadou

    I How do we compute an integral with a dot product inside ?

    I was trying to solve a problem involving work , as we know : w = \int_{a}^{b} \vec{f}.d\vec{s} but in my problem the path was cyrcular , so how to evaluate this kind of integral ?
  42. F

    Surface Integral Homework: Is the Author's Solution Wrong?

    Homework Statement Is the solution provided by the author wrong ? Stokes theorem is used to calculate the line integral of vector filed , am i right ? Homework EquationsThe Attempt at a Solution To find the surface integral of many different planes in a solid , we need to use Gauss theorem ...
  43. karush

    MHB Integral of a rational function

    $\textsf{evaluate}$ \begin{align} \displaystyle {I}&={\int{\frac{x+2}{x^2+1}dx}}\\ &=\int{\frac{x}{x^{2}{+1}}dx{\ +\ 2}\int{\frac{1}{x^{2}{+1}}}}{\ }dx\\ u&=x^{2}+1 \therefore \frac{1}{2x}du=dx\\ x&=\sqrt{u-1}\\ \end{align} ...? $\textit{calculator answer.?}$ $\dfrac{\ln\left(x^2+1\right)}{2}...
  44. Rectifier

    Antiderivative of a rational function

    I am trying to find primitives to the rational function below but my answer differs from the answer in the book only slightly and now, I am asking for your help to find the error in my solution. This solution is long since I try to include all the steps in the process. The problem $$ \int...
  45. J

    MHB Integral of Fresnel functions

    I have been working on this for several days but getting nowhere. Any help would be great. \begin{align} &\int_0^x dy\,y^2 \cos(y^2) C^2 \!\!\left(\!\frac{\sqrt{2}\,y}{\sqrt\pi}\!\right) \end{align} In reality only the first one is causing me troubles, however I have pasted the entire...
  46. bwest121

    How do I calculate this integral?

    Homework Statement We're given the gaussian distribution: $$\rho(x) = Ae^{-\lambda(x-a)^2}$$ where A, a, and ##\lambda## are positive real constants. We use the normalization condition $$\int_{-\infty}^{\infty} Ae^{-\lambda(x-a)^2} \,dx = 1$$ to find: $$A = \sqrt \frac \lambda \pi$$ What I want...
  47. ShayanJ

    A Path integral formula for vacuum to vacuum amplitude

    I'm reading the path integral chapter of Schwartz's "Quantum Field theory and the Standard model". Something seems wrong! He starts by putting complete sets of states(field eigenstates) in between the vacuum to vacuum amplitude: ## \displaystyle \langle 0;t_f|0;t_i \rangle=\int D\Phi_1(x)\dots...
  48. BiGyElLoWhAt

    Solving for the Green's Function and Using It to Solve an Differential Equation

    Homework Statement Find the green's function for y'' +4y' +3y = 0 with y(0)=y'(0)=0 and use it to solve y'' +4y' +3' =e^-2x Homework Equations ##y = \int_a^b G*f(z)dz## The Attempt at a Solution ##\lambda^2 + 4\lambda + 3 = 0 \to \lambda = -1,-3## ##G(x,z) = \left\{ \begin{array}{ll} Ae^{-x}...
  49. BiGyElLoWhAt

    Green's Function and integral

    Homework Statement Find the green's function for y'' +2y' +2y = 0 with boundary conditions y(0)=y'(0)=0 and use it to solve y'' + 2y' +2y = e^(-2x) Homework Equations ##y = \int_a^b G(x,z)f(z)dz## The Attempt at a Solution I'm going to rush through the first bit. If you need a specific step...
  50. Rectifier

    Integration with variable substitution

    Hello, I am having trouble with solving the problem below The problem Find all primitive functions to ## f(x) = \frac{1}{\sqrt{a+x^2}} ##. (Translated to English) The attempt I am starting with substituting ## t= \sqrt{a+x^2} \Rightarrow x = \sqrt{t^2 - a} ## in $$ \int \frac{1}{\sqrt{a+x^2}}...
Back
Top