What is Integral: Definition and 1000 Discussions

In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with differentiation, integration is a fundamental, essential operation of calculus, and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others.
The integrals enumerated here are those termed definite integrals, which can be interpreted formally as the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Conventionally, areas above the horizontal axis of the plane are positive while areas below are negative. Integrals also refer to the concept of an antiderivative, a function whose derivative is the given function. In this case, they are called indefinite integrals. The fundamental theorem of calculus relates definite integrals with differentiation and provides a method to compute the definite integral of a function when its antiderivative is known.
Although methods of calculating areas and volumes dated from ancient Greek mathematics, the principles of integration were formulated independently by Isaac Newton and Gottfried Wilhelm Leibniz in the late 17th century, who thought of the area under a curve as an infinite sum of rectangles of infinitesimal width. Bernhard Riemann later gave a rigorous definition of integrals, which is based on a limiting procedure that approximates the area of a curvilinear region by breaking the region into thin vertical slabs.
Integrals may be generalized depending on the type of the function as well as the domain over which the integration is performed. For example, a line integral is defined for functions of two or more variables, and the interval of integration is replaced by a curve connecting the two endpoints of the interval. In a surface integral, the curve is replaced by a piece of a surface in three-dimensional space.

View More On Wikipedia.org
Recent contents Top users
  1. W

    Mathematica Is the integral for current correct?

    Hi, I am using Mathematica to calculate density of states and current of the Green's function times self energy in most simple form. I am not sure if I am getting current integral over energy implemented correctly. Shouldnt first current plot be a line with a slope? Below is my code...
  2. B

    I How to calculate Miits (quench integral)?

    How to find the value of miits integral for calculations of the propagation of normal zonei in superconductors?
  3. karush

    MHB 206.08.08.10 integral from --\infty

    \tiny{206.08.08.10 } \begin{align*} \displaystyle I&= \int_{-\infty}^{0}\frac{dx}{(x+2)^{1/3}}\\ &=-\infty\\ \end{align*} why does this go to $-\infty$
  4. B

    A Integral representation of Euler constan

    I am working on the integral representation of the Euler-Mascheroni constant and I can't seem to understand why the first of the two integrals is (1-exp(-u))lnu instead of just exp(-u)lnu. It is integrated over the interval from 1 to 0, as opposed to the second integral exp(-u)lnu which is...
  5. S

    I Solving Complex Integral Paths - Real Line Poles

    Hello! If I have a real integral between ##-\infty## and ##+\infty## and the function to be integrated is holomorphic in the whole complex plane except for a finite number of points on the real line does it matter how I make the path around the poles on the real line? I.e. if I integrate on the...
  6. Anshul23

    Highschool graduate dealing with a triple integral?

    I recently came across a problem in Irodov which dealt with the gravitational field strength of a sphere. Took some time to get my head around it and figure how to frame a triple integral, but it felt good at the end. Am I going to start seeing triple integrals in the freshman year tho? If so...
  7. DavideGenoa

    I Differentiation under the integral in retarded potentials

    Hello, friends! I know, thanks to @Hawkeye18 who proved this identity to me, that, if ##\phi:V\to\mathbb{R}## is a bounded measurable function defined on the bounded measurable domain ##V\subset\mathbb{R}^3##, then, for any ##k\in\{1,2,3\}##, $$\frac{\partial}{\partial r_k}\int_V...
  8. M

    I Understanding a Time Integral for x1 and x2

    Hello everyone. Iam trying to get my head around a solution for an integral but I can't figure out how its done. I have given the following : x1'(t) = 0 x2'(t) =tx1(t) Where " ' " indicates the derivative. Talking the time integral the result is given by: x1(t) = x1(t0) x2(t) =...
  9. Z

    B Solving Indefinite Integrals: A Beginner's Guide

  10. S

    Integral Equation (or I think so) Calculus I problem

    Homework Statement Find a continuous funciton ##f## such that $$ f(x) = 1+ \dfrac{1}{x} \int_{1}^{x} f(t)dt $$ I think I solved it but I would like to see if it's right. Well, first of all, by the fundamental theorem of calculus I know that $$ \left( \int_{1}^{x} f(t)dt \right) ' = f(x) $$...
  11. SamRoss

    B Not following an integral solution

    In the image below, why is the third line not \frac {ln(cosx)} {sinx}+c ? Wouldn't dividing by sinx be necessary to cancel out the extra -sinx that you get when taking the derivative of ln(cosx)? Also, wouldn't the negatives cancel?
  12. H

    B Definite integrals with +ve and -ve values

    I understand that if you have a function in which you want to determine the full (i.e. account for positive and negative values) integral you need to break down your limits into separate intervals accordingly. Is there any way in which you can avoid this or is it mathematically impossible? If...
  13. S

    I Prove Complex Integral: $\int_m^\infty\sqrt{x^2-m^2}e^{-ixt}dx$

    Hello! I found a proof in my physics books and at a step it says that: ##\int_m^\infty\sqrt{x^2-m^2}e^{-ixt}dx \sim_{t \to \infty} e^{-imt}##. Any advice on how to prove this?
  14. C

    REDUZE for Feynman integral tensor reduction

    I was wondering if anyone knows how to set up a procedure in REDUZE that will decompose tensor integrals appearing in QCD loop calculations into a sum of scalar topologies with the tensor structure factored out? I've had a look at the appropriate manual but I am not entirely sure how to...
  15. R

    Line integral of vector field from Apostol calculus

    Homework Statement Here are the three problems that i couldn't solve from the book Calculus volume 2 by apostol 10.9 Exercise 2. Find the amount of work done by the force f(x,y)=(x^2-y^2)i+2xyj in moving a particle (in a counter clockwise direction) once around the square bounded by the...
  16. The_eToThe2iPi

    I Limitations of the Lebesgue Integral

    So I'm studying a course on measure theory and we've learned that the Lebesgue integral of a real function is (loosely) defined as the total area over the x-axis minus the total area under the x-axis. This seems to me to be limited because these areas can both be infinite but their difference...
  17. R

    How to properly solve question 2,4,5?

    1. Homework Statement Guys I am struggling with question 2,4,5 I had upload the question and my attempt. I had been re doing for several times with same answer not match with the model answer, please show me the correct way of solving it Homework EquationsThe Attempt at a Solution
  18. R

    Integral simplification using Bessel functions

    Homework Statement I need to simplify the following integral $$f(r, \theta, z) =\frac{1}{j\lambda z} e^{jkr^2/2z} \int^{d/2}_0 \int^{2\pi}_0 \exp \left( -\frac{j2\pi r_0 r}{z\lambda} \cos \theta_0 \right) r_0 \ d\theta_0 dr_0 \tag{1}$$ Using the following integrals: $$\int^{2\pi}_0 \cos (z...
  19. C

    Improper integral with spherical coordinates

    Homework Statement I have a question. I have a function f(x,y,z) which is a continuous positive function in D = {(x,y,z); x^2 + y^2 +z^2<=1}. And let r = sqrt(x^2 + y^2 + z^2). I have to check whether the following jntegral is convergent. x^2y^2z^2/r^(17/2) * f(x,y,z)dV. Homework Equations...
  20. P

    MHB Luca's question via email about a line integral....

    I am assuming that this line integral is along the straight line from $\displaystyle \begin{align*} (0,0,0) \end{align*}$ to $\displaystyle \begin{align*} \left( 5, \frac{1}{2}, \frac{\pi}{2} \right) \end{align*}$, which has equation $\displaystyle \begin{align*} \left( x, y, z \right) = t\left(...
  21. harpazo

    MHB How do I evaluate this triple integral for 2ze^(-x^2) over the given bounds?

    Evaluate the triple integral. Let S S S = triple integral The function given is 2ze^(-x^2) We are integrating over dydxdz. Bounds pertaining to dy: 0 to x Bounds pertaining to dx: 0 to 1 Bounds pertaining to dz: 1 to 4 S S S 2ze^(-x^2) dydxdz S S 2yze^(-x^2) from y = 0 to y = x dxdz S...
  22. harpazo

    MHB Volume for Triple Integral

    Use a triple integral to find the volume of the solid bounded by the graphs of the equations. x = 4 - y^2, z = 0, z = x I need help setting up the triple integral for the volume. I will do the rest.
  23. R

    Line integral problems in Apostol calculus

    Homework Statement A two dimensional force field f is give by the equation f(x,y)=cxyi+x^6 y^2j, where c is a positive constant. This force acts on a particle which must move from (0,0) to the line x=1 along a curve of the form y=ax^b where a>0 and b>0 Homework Equations Find a value of a(in...
  24. R

    Is there any way to calculate this integral?

    I have done it by the parametric form of σ, but if I change σ to implicit form that is G(x,y,z)=x^2+y*2+z^2-R^2=0 I don't know how continue. The theory is: where Rxy is the projection of σ in plane xy so it's the circumference x^2+y^2=R^2
  25. S

    B Some help understanding integrals and calculus in general

    So in differential calculus we have the concept of the derivative and I can see why someone would want a derivative (to get rates of change). In integral calculus, there's the idea of a definite integral, which is defined as the area under the curve. Why would Newton or anyone be looking at the...
  26. Q

    Mathematica Mathematica: Convolution Integral

    Hi all! I'm new to Mathematica. I have written a code for performing a convolution integral (as follows) but it seems to be giving out error messages: My code is: a[x_?NumericQ] := PDF[NormalDistribution[40, 2], x] b[k_?NumericQ, x_?NumericQ] := 0.0026*Sin[1.27*k/x]^2 c[k_?NumericQ...
  27. Pushoam

    I Corollaries of the fundamental integral theorems

    Can anyone please tell me significance of these corollaries of fundamental integral theorems? I can prove these corollaries but I don't understand why do we need to learn it? Do these corollaries have some physical significance? (a)$$\iiint_V(\nabla T)d^3 x=\oint_S T d\vec a$$ here S is the...
  28. C

    Integral with transformations and bounded by x + y + z = 1

    Homework Statement I have a question. I need to know the integral dxdydz/(y+z) where x>=0, y>=0, z>=0.Homework Equations It is bounded by x + y + z = 1. The transformations I need to use are x=u(1-v), y=uv(1-w), z=uvw. The Attempt at a Solution y+z = uv. J = uv(v-v^2+uv) So I get the integral...
  29. yecko

    Solve Improper Integral Homework - Get Help Now!

    Homework Statement https://holland.pk/uptow/i4/7d4e50778928226bfdc0e51fb64facfb.jpg Homework Equations improper integral The Attempt at a Solution (attached) Whats wrong with my calculation? I cannot figure it out after hours... Thank you very much!
  30. Mr Davis 97

    How Do You Choose the Correct Polar Coordinates for Surface Integrals?

    Homework Statement Solve the surface integral ##\displaystyle \iint_S z^2 \, dS##, where ##S## is the part of the paraboloid ##x=y^2+z^2## given by ##0 \le x \le 1##. Homework EquationsThe Attempt at a Solution First, we make the parametrization ##x=u^2+v^2, \, y=u, \, z = v##, so let...
  31. K

    A Difficult cosh integral using Leibniz rule?

    I was wondering if I could get some pointers on how to at least start on this. In quantum mechanics we are using the WKB approximation, and we end up with a definite integral that looks like this: ∫(1 - a(cosh(x))-2)1/2 dx = ∫(1/cosh(x)) (1 - a(cosh(x))2)1/2 dx where a is a positive constant...
  32. grandpa2390

    How did my professor get this integral

    Homework Statement derive maxwell distribution function in case of 1-d and 2-d classical gas Homework EquationsThe Attempt at a Solution [/B] The constant K can be solved from normalization. ##\int_{-∞}^{∞} F(V_x)dV_x = 1## substituting ##F(V_x)=Ke^{+/- kV_x^2}## ##1 = K\int_{-∞}^{∞}...
  33. harpazo

    MHB Iterated Integral in Polar Coordinates

    Evaluate the iterated integral by converting to polar coordinates. Let S S = interated integral symbol S S xy dy dx The inner integral limits are 0 to sqrt{2x - x^2}. The outer integral limits are 0 to 2. Solution: I first decided to rewrite sqrt{2x - x^2} in polar form. So, sqrt{2x -...
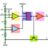
  34. Alexanddros81

    Why an integral vanishes? Angular momentum of a rigid body

    Hi. I am revising my Mechanics: Dynamics by reading the Beer 10th edition textbook and Pytel 2nd edition In Pytel pg 358 art. 17.3 the angular momentum about the mass center of a rigid body in general motion is being calculated...
  35. S

    I Complex integral of a real integrand

    I am trying to do the following integral: $$\int_{\pi f}^{3\pi f} dx \sqrt{\cos(x/f)}.$$ Wolfram alpha - http://www.wolframalpha.com/input/?i=integrate+(cos(x))^(1/2)+dx+from+x=pi+to+3pi gives me $$\int_{\pi f}^{3\pi f} dx \sqrt{\cos(x/f)} = 4f E(2) = 2.39628f + 2.39628if,$$ where E is the...
  36. K

    How Does the Fundamental Theorem of Calculus Apply to Derivatives of Integrals?

    Homework Statement Homework Equations $$F(x)=\int_a^x f(x),~~F'(x)=f(x)$$ The Attempt at a Solution In F'(x), x is at the end of the domain a-x, so, in my function ##~\cos(x^2)~## i also have to take the end of the domain, and it's 2x, so F'(x)=cos(4x2), but it's not enough. The answer is...
  37. R

    Integral form of Particular solution question

    Homework Statement I'm fine with the first part. Part b) is causing me trouble http://imgur.com/xA9CG5G Homework EquationsThe Attempt at a Solution I tried subbing in the solution y1 into the given equation, but I'm not sure how to differentiate this, i thought of using integration by parts...
  38. A

    Integral of unit impulse function?

    Homework Statement let's use this symbol to denote the unit impulse function δ When integrating the unit impulse function (from negative infinity to infinity) ∫δ(t) dt I know that this results in a value of 1 and is only nonzero at the point t = 0. However for example take this integral into...
  39. K

    Why 1/2 is Coefficient in CK Sum for Integrals

    Homework Statement Why specifically 1/2 is the coefficient in CK? the sum, basically, doesn't change except for the coefficient. i can choose it as i want. I understand the sum must equal the integral but i guess that's not the reason Homework Equations Area under a curve as a sum...
  40. T

    Another Improper Integral Using Complex Analysis

    Homework Statement $$\int_{-\infty}^\infty \space \frac{cos(2x)}{x-3i}dx$$ Homework EquationsThe Attempt at a Solution $$\int_{-R}^R \space \frac{e^{2ix}}{x-3i}dx + \int_{C_R} \space \frac{e^{2iz}}{z-3i}dz = 2\pi i\sum\space res \space f(z)$$ Then using Jordan's Lemma, as ##R\to\infty## the...
  41. T

    Improper Integral Using Complex Analysis

    Homework Statement Compute the Integral: ##\int_{-\infty}^\infty \space \frac{e^{-2ix}}{x^2+4}dx## Homework Equations ##\int_C \space f(z) = 2\pi i \sum \space res \space f(z)## The Attempt at a Solution At first I tried doing this using a bounded integral but couldn't seem to get the right...
  42. M

    Integral of absolute value of a Fourier transform

    Homework Statement Hi guys, I am going to calculate the following integral: $$\int_0^{f_c+f_m} |Y(f)|^2\, df$$ where:$$Y(f)=\frac{\pi}{2} \alpha_m \sum_{l=1}^{L} \sqrt{g_l}\left [ e^{-j(\omega \tau_l - \theta_m)} \delta(\omega - \omega_0) + e^{-j(\omega \tau_l + \theta_m)} \delta(\omega +...
  43. C

    Residue Theorem: Finding the Integral of z^3e^(-1/z^2) over |z|=5

    Homework Statement use the residue theorem to find the value of the integral, integral of z^3e^{\frac{-1}{z^2}} over the contour |z|=5 The Attempt at a Solution When I first look at this I see we have a pole at z=0 , because we can't divide by zero in the exponential term. and a pole of...
  44. JulienB

    Calculating Planck's integral for finite range of wavelength

    Homework Statement Hi everybody! I am asked to calculate how much of the total radiated power of a light bulb at temperature ##T=2300##K is contained within ##400##nm and ##750##nm. I am also given the average emissivity of tungsten ##\epsilon_\text{ave}=0.288## and the emissivity within the...
  45. K

    Integral of a area under a straight line as summation

    Homework Statement Homework Equations Summs: $$1+2+3+...+n=\frac{n(n+1)}{2}$$ $$1^2+2^2+3^2+...+n^2=\frac{n(n+1)(2n+1)}{6}$$ The Attempt at a Solution $$\Delta x=\frac{b}{n}$$ $$S_n=f\left( \frac{\Delta x}{2} \right)\Delta x+f\left( \Delta x+\frac{\Delta x}{2} \right)\Delta x+...+f\left(...
  46. A

    How Do You Determine Integration Limits for Convolution Integrals?

    Homework Statement Hi all, I hope you all can help me so I'm studying for my signals course and I encounter this example in the book, and the answer is there but the solution isn't... The convolution integral exists for 3 intervals and I could evaluate the first two just fine... however I can't...
  47. J

    MATLAB Octave integral computation help

    Hello, I'm having some trouble with my octave coding and would appreciate any input on where the issue lies. The coding is as follows: age = [0:1:100]; %this is the age matrix, represented by a time = [0:1:100]; %this is the time matrix...
  48. Emmanuel_Euler

    A What is the relationship between cos(cosx) and Bessel functions?

    Hi everyone, my friend challenged me to solve this definite integral...integral from -2pi to 2pi ((sin(2sinx)+cos(2cosx))dx, i proved by using definite integral properties that this integral equals to integral from -2pi to 2pi cos(2cosx)dx, can you give me any ideas how to solve this?? I know...
  49. dumbdumNotSmart

    Heat equation integral - Fourier Series coefficient is zero

    Homework Statement WE have a thermally insulated metallic bar (from enviroment/surroundings) . It has a temperature of 0 ºC. At t=0 two thermal sources are applied at either end, the first being -10 ºC and the second being 10 ºC. Find the equation for the temperature along the bar T(x,t), in...
  50. Vitani11

    Calculate the volume integral of divergence over a sphere

    Homework Statement For the vector field F(r) = Ar3e-ar2rˆ+Br-3θ^ calculate the volume integral of the divergence over a sphere of radius R, centered at the origin. Homework Equations Volume of sphere V= ∫∫∫dV = ∫∫∫r2sinθdrdθdφ Force F(r) = Ar3e-ar2rˆ+Br-3θ^ where ^ denote basis (unit vectors)...
Back
Top