You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What is Microcanonical ensemble: Definition and 18 Discussions
In statistical mechanics, the microcanonical ensemble is a statistical ensemble that represents the possible states of a mechanical system whose total energy is exactly specified. The system is assumed to be isolated in the sense that it cannot exchange energy or particles with its environment, so that (by conservation of energy) the energy of the system does not change with time.
The primary macroscopic variables of the microcanonical ensemble are the total number of particles in the system (symbol: N), the system's volume (symbol: V), as well as the total energy in the system (symbol: E). Each of these is assumed to be constant in the ensemble. For this reason, the microcanonical ensemble is sometimes called the NVE ensemble.
In simple terms, the microcanonical ensemble is defined by assigning an equal probability to every microstate whose energy falls within a range centered at E. All other microstates are given a probability of zero. Since the probabilities must add up to 1, the probability P is the inverse of the number of microstates W within the range of energy,
P
=
1
/
W
,
{\displaystyle P=1/W,}
The range of energy is then reduced in width until it is infinitesimally narrow, still centered at E. In the limit of this process, the microcanonical ensemble is obtained.
View More On Wikipedia.org
The primary macroscopic variables of the microcanonical ensemble are the total number of particles in the system (symbol: N), the system's volume (symbol: V), as well as the total energy in the system (symbol: E). Each of these is assumed to be constant in the ensemble. For this reason, the microcanonical ensemble is sometimes called the NVE ensemble.
In simple terms, the microcanonical ensemble is defined by assigning an equal probability to every microstate whose energy falls within a range centered at E. All other microstates are given a probability of zero. Since the probabilities must add up to 1, the probability P is the inverse of the number of microstates W within the range of energy,
P
=
1
/
W
,
{\displaystyle P=1/W,}
The range of energy is then reduced in width until it is infinitesimally narrow, still centered at E. In the limit of this process, the microcanonical ensemble is obtained.
View More On Wikipedia.org
-

Microcanonical ensemble generalized pressure
In the discussion of the pressure in macrocanonical ensemble, I found in textbook that: ##dW = \bar p dV## (##dW## is in fact d_bar W, yet I can't type the bar) The derivation goes like: ##\bar p = \frac{1}{Z} \sum_{r} e^{-\beta E_r} (-\frac{\partial E_r}{\partial V}) = ... = \frac{1}{\beta}...- Mayan Fung
- Thread
- Replies: 2
- Forum: Mechanics
-
L
Why is the entropy calculated differently in the microcanonical ensemble?
I have a problem to understand why this problem is microcanonical ensemble problem? And why entropy is calculated as S(E,N,V)=\ln \Gamma(E,N,V) When in microcanonical ensemble we spoke about energies between ##E## and ##E+\Delta E##.- LagrangeEuler
- Thread
- Replies: 8
- Forum: Advanced Physics Homework Help
-
C
Phase space volume with a potential (microcanonical ensemble)
I don't know how to solve that integral, and to calculate the number of microstates first, then aply convolution and then integrate to find the volume of the phase space seems to be more complicated. Any clue on how to solve this? Thank you very much.- Cleo
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-

Partition Function of N particles in an assymetrical box
Homework Statement Consider a gas sufficiently diluted containing N identical molecules of mass m in a box of dimensions Lx, Ly, Lz. Calculate the probability of finding the molecules in any of their quantum states. Calculate the energy of each quantum state εr, as a function of the quantum... -

Demon algorithm for microcanonical ensemble
I simulated a microcanonical ensemble of 10 ideal gas particles in one dimension and yielded the expected normal distribution of velocities. However, I still did not get how the algorithm works. The demon has non-negative energy content and the demon together with the system constitutes a closed...- gre_abandon
- Thread
- Replies: 3
- Forum: Atomic and Condensed Matter
-
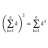
Microcanonical partition function - Dirac delta of operators
Homework Statement Why is it that the microcanonical partition function is ##W = Tr\{\delta(E - \hat{H})\}##? As in, for example, Mattis page 62? Moreover, what's the meaning of taking the Dirac delta of an operator like ##\hat{H}##? Homework Equations The density of states at fixed energy is...- ddd123
- Thread
- Replies: 2
- Forum: Advanced Physics Homework Help
-

Microcanonical ensemble question
So from what I understood from some coure notes I've been reading, a microcanonical ensemble is a situation where we have an isolated system in thermal equilibrium with a constant given N,V,E - particles, volume,total energy. I'm a bit confused. How I understood 'ensemble' is as a set of all...- Coffee_
- Thread
- Replies: 3
- Forum: Classical Physics
-
S
Microcanonical ensemble density matrix
Ref: R.K Pathria Statistical mechanics (third edition sec 5.2A) First it is argued that the density matrix for microcanonical will be diagonal with all diagonal elements equal in the energy representation. Then it is said that this general form should remain the same in all representations. i.e...- Seban87
- Thread
- Replies: 20
- Forum: Quantum Physics
-
S
Microcanonical ensemble density matrix
Ref: R.K Pathria Statistical mechanics (third edition sec 5.2A) First it is argued that the density matrix for microcanonical will be diagonal with all diagonal elements equal in the energy representation. Then it is said that this general form should remain the same in all representations. i.e...- Seban87
- Thread
- Replies: 2
- Forum: New Member Introductions
-
N
Microcanonical Ensemble: Unequal Weighting of Points
Hello, I was wondering if it is a well known fact that the microcanonical ensemble (i.e. W = \int \delta(\mathcal H(\vec x, \vec p) - E) \mathrm d \vec x \mathrm d \vec p) does not weight every point equally, in the sense that in the integral (which was just quoted) some points on the energy...- nonequilibrium
- Thread
- Replies: 1
- Forum: Mechanics
-
D
Microcanonical ensemble, density operator
hi, usually the density operator for the microcanonical ensemble is given by \rho = \sum_n p_n|n><n| where |n> are energy eigenstates and p_n is the probability that our system is in this state. p_n = const. if the energy corresponding to |n> is in the energy inteval (E,E+∆E)...- Derivator
- Thread
- Replies: 6
- Forum: Quantum Physics
-
E
Microcanonical ensemble for system of harmonic oscillators
Homework Statement A system consists of 3N (N >> 1) independent, identical, but distinguishable one-dimensional oscillators. This is relevant in that the atoms in a solid are sitting around their equilibrium positions. Assume that every atom constitutes an independent oscillator and all...- everyday847
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
F
Ideal gas in the microcanonical ensemble - a subtle point?
Hi all, I was brushing up on statistical ensembles, and I found something apparently weird in microcanonical treatment of the ideal "classical" gas. I'm mainly following K. Huang's Statistical Mechanics. So there's a first approach to the problem in which the MC entropy is evaluated via an...- FranzDiCoccio
- Thread
- Replies: 14
- Forum: Classical Physics
-
F
Ideal gas in the microcanonical ensemble: I'm puzzled
Hi all, this is about problem 8.2 in Huang's Statistical Mechanics. I think I've been able to solve it, but the solution raised a question about the Maxwell-Boltzmann distribution. So first I provide my solution to the problem, then discuss the apparently weird point. Homework...- FranzDiCoccio
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
N
Microcanonical ensemble question
Homework Statement The entropy in the microcanonical ensemble is defined in terms of omega(E), the number of states such that total energy be E. compute (as a function of total energy E,total number of particles N and magnetic field h) N+ the number of particles i with sigma= +1 and N- where...- Nathan Davies
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
L
Forming an Ice Sheet on a Lake: Microcanonical Ensemble
Homework Statement An ice sheet forms on a lake. The air above the lake is at \Delta T (<0), while the water below the ice sheet is at 0°C. Assume that the heat of fusion of the water freezing on the lower surface is conducted through the sheet to the air above. How much time does it take to...- luisgml_2000
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
S
Microcanonical ensemble with four spin 1
Four spin1 particles are rigidly fixed at four corners of a square. 1. What will be the entropy. 2. A field is now applied that produces an energy difference between m=0 and m=1,-1 states of each of each particle. Take m=0 as the ground state and find the free energy at temperature T. 3. Find...- souvik.manoj
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
P
Microcanonical ensemble => constant entropy?
Homework Statement In a microcanonical ensemble is entropy constant? Since there is only one macrostate of energy. The Attempt at a Solution I think so.- pivoxa15
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help