Approximate LCDM Expansion in Simplified Math (Part 2)

Part 2: Time and Distance

In Part 1 we have seen how one of the simplest ways of expressing the fractional expansion rate of the universe, i.e. the Hubble value H, is with this equation:

2.1 [itex]H = (0.44 S^3+1)^{0.5}[/itex] zeit^-1

Here S is the ‘stretch factor’, which is the inverse of the scale factor a, i.e. S=1/a. By convention, S have a present value of 1.0; hence the present Hubble value H₀ = (1.44)^0.5 = 1.2 zeit^-1.  But what is the relationship between H and cosmological time?

Cosmological Time

Because of the instantaneous “interest on interest” nature of cosmic expansion, it follows an exponential pattern (e^Ht), provided that H remains constant over time. Presently H is still decreasing, so cosmological time is approximated by the following natural logarithmic equation:^[1]

(2.2) [itex]\large t = \frac{1}{3}\ln(\frac{H+1}{H-1})[/itex] zeit.

Let us put our present H₀ = 1.2 zeit^-1 in here (using Google or some other calculator) and check that we get the 0.8 zeit that we expect.

[itex]t_{now} = \frac{1}{3}\ln(\frac{2.2}{0.2})\approx 0.8[/itex] zeit.

Suppose we observe the redshift from a specific galaxy as z=1, which means that the light has left it when the wavelength stretch factor was S = z+1 = 2. Plugging S = 2 into eq. 2.1, we find that H = 2.13 zeit^-1 when the light was emitted. The cosmic time was

[itex]t_{then} = \frac{1}{3}\ln(\frac{2.13+1}{2.13-1})\ = 0.34[/itex] zeit after the start of the present expansion.^[2]

The light from that galaxy obviously took 0.8 – 0.34 = 0.46 zeit to reach us – it is the so-called ‘lookback time’.

Now that we have a feeling for the relationships, what is better than viewing it on a graph? Here you see the parameters mentioned so far (against time).

Fig: 2.1: Scale factor (a) , Stretch factor (S) and Hubble value (H) against time

You can see our present time (0.8 zeit) clearly where the red and blue curves cross, i.e. where both S and a are unity. You can also see how H starts high and asymptotically approaches unity. The graphs were plotted using LightCone 7zeit, a variant of the standard LightCone 7.

I have ‘sneaked in’ the curve for the scale factor (a=1/S), but I did not give a direct relationship of it against time yet. You get it by solving eqs. 2.1 and 2.2 simultaneously, which is not a simple exercise at all. Fortunately, mathematics comes to the rescue and we have a nifty solution for a(t), i.e. the scale factor as a function of time:

(2.3) [itex]\Large a(t) = \frac{\sinh^{2/3}(\frac{3}{2}t)}{1.3} [/itex]

where sinh is the hyperbolic sine function. The ‘hypersine’ is obviously related to the natural logarithm ln(x) and the natural exponent (e^x). The factor 1.3 is just scaling to make a_now = 1 at t_now = 0.8 zeit, as is the convention. The importance of a(t) is that its curve shows how a decelerating expansion gradually changed over to an accelerating expansion. The inflection point can be visually judged to lie between 0.4 and 0.5 zeit. It is actually at 0.44 zeit.

Proper Distance

Proper distance in cosmology is like measuring distance on a hypothetical frozen view of the cosmos, i.e. with expansion stopped. Obviously, we cannot stop expansion, so how do we find proper distance? There are various methods, but once we have the present and long-term Hubble values (H₀ and H_∞), we only need to measure the redshift of a source and then calculate its proper distance from where we are.

Because of the non-linear expansion, there is no precise analytical solution for the proper distance (that I know of). We have to numerically integrate into small steps, but fortunately the definite integral is rather neat:

(2.4) [itex]\large D_{now} = \int_1^S{\frac{dS}{H}} = \int_1^S{\frac{ds}{\sqrt{0.44S^3+1}}}[/itex]

We have substituted H from eq. 2.1 in here, so that we have a distance in terms of the observable S = z+1. For calculation, you can use your favorite integrator, but a rather cool web-based one is available at

http://www.numberempire.com/definiteintegralcalculator.php.

For our previous sample galaxy at S=2, I entered 1/sqrt(0.443x^3+1) into the Function box, with 1 in the “From” and 2 in the “To” boxes and then clicked “Compute” – it returned the answer as 0.64, which in our cas has the units lightzeit. So we receive the light when the proper distance to the galaxy is D_now = 0.64 lzeit. Since we have used stretch S = 2, the proper distance when the photons left the galaxy was half of 0.64, i.e. 0.32 lzeit; so we say that D_then = 0.32 lzeit for this galaxy.  Recall that the light left that galaxy at t = 0.34 zeit, i.e. 0.46 zeit ago. Here is a graph of D_now and D_then.

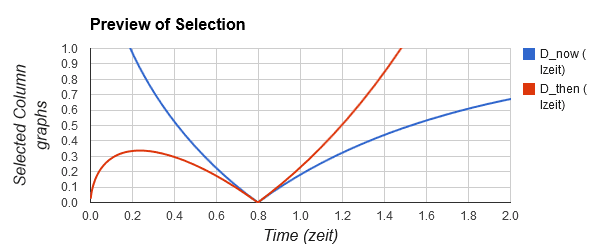
Fig. 2.2: Present proper distance (D_now, also called the comoving distance) and the proper distance when light was emitted, or will be received (D_then, also called the past and future lightcones).

The red D_then curve is also known as the cosmological lightcone. To the left of 0.8 zeit it represents our past lightcone and to the right of 0.8 zeit our future lightcone. Near t = 0.0 the universe was very dense and objects we now observe were actually very, very close to our space locality. Distances then grew much faster than the progress that photons could make in our direction and ancient photons were at first dragged away from us. At around t = 0.23 zeit, the fractional expansion rate dropped enough to allow photons to make progress and eventually reach our telescopes.

To summarize, we have now looked at a further three rather easy equations that allow us to calculate the most common values for the standard cosmological model.

Part 3 will deal with the Hubble radius and two cosmological horizons that we should take notice of.

End-notes

[1] The function e^Ht gives the factor by which cosmic distances increase in a time interval t, provided that H remains constant over this time interval. In the far future, H will be a constant, but in the early universe H changed significantly over periods longer than a million years. Hence the more complex general solution.

[2] To verify that the approximations are valid, I used the LightCone 7zeit calculator for a ‘one-shot’ calculation with S_upper=2 and S_step=0.

[3] The D_then lightcone is where the LightCone 7 calculator got its name from.