Assessing the Physics in Edmond Hamilton’s “The Second Satellite”

This article won’t contain much about physics that typical readers of this site don’t already know. However,  deconstructing improper physics in literature and film can be a good exercise for physics teachers to share with their students. I’ll focus on one story, in particular, Edmond Hamilton’s The Second Satellite.

Second Satellite Key Points

1. The article focuses on Edmond Hamilton‘s 1930 short story “The Second Satellite“
2. The protagonist of the story concludes that the aviators disappeared due to their planes being swept up by a secondary moon orbiting close to the Earth
3. The story provides clues to determine the orbit and properties of the planet but when pieced together, they don‘t add up
4. The calculated orbital period of the satellite is 6 hours and the predicted height of the satellite is 18,000 km
5. From Earth, the satellite would look very large, taking up the entire sky when overhead
6. Gravity on the satellite would be 1/166th of Earth‘s gravity and it likely wouldn‘t have a bound atmosphere
7. The tidal force of the satellite on Earth is 5,000 times that of the moon and would obliterate the planet
8. Hamilton likely made up numbers as he went along without much concern for accuracy

Just for a bit of context, I’ll explain why I came to think about this particular story. One of the things I do to help myself fall asleep is to listen to audiobooks of public-domain science fiction short stories. I play the stories from my phone, visualize them in my head, and eventually (ideally) pass out. It can take me months to get through a single story because I keep falling asleep before they’re finished. I find these audiobooks on Librivox.org in their sci-fi collection and typically read things that are read by Gregg Margarite. A lot of these stories were written for pulp magazines between the 30s and the 60s and often feature anachronisms based on the knowledge of the time, envisioning space travel before Sputnik or assuming that the Cold War would continue into the era of interstellar exploration. Not all of these stories are good, but to fall asleep, they don’t necessarily have to be.

Lately, I have been listening to a story called The Second Satellite, written by Edmond Hamilton in 1930 and appearing in Astounding Stories of Super Science. At the time I was writing this article, I still hadn’t gotten to the end, and I’ve been on it for quite some time. You can read the story here or listen to it here. The story is about some aviators who are trying to break the altitude record, getting above 30 miles in their fictional technology aircraft. Some of the aviators have inexplicably disappeared, and the protagonist surmises that it’s because their planes were swept up by a secondary moon that orbits very close to the Earth. They go up and try to find it and end up landing on the moon. Then it gets a little weird, they find that it’s inhabited by a race of frog vampires that enslave green humans for their blood.

 

Throughout the story, several clues are given to determine the orbit and properties of the planet. However, when you try to piece all of these together, they don’t add up.

The story starts with a discussion about the four aviators that had disappeared. It is stated that they disappeared over Baja California, Sweden, Long Island, and Australia. The protagonist concludes that these lie on a Great Circle, a circle with the same circumference as the equator. From this, he concludes that this is consistent with the planes getting swept up by the satellite. I used a website called scribblemaps.com to draw Great Circles on a map…it’s pretty hard to get them to go through the points you want. While I could get a straight line (on a rectangular projection) through the four locations of interest (Australia being big enough to give some leeway), I was unable to get a Great Circle to Sweden.

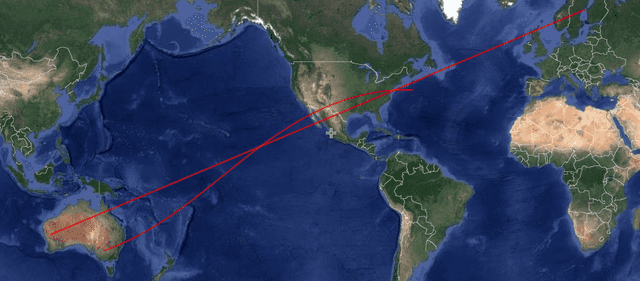
Trying to draw a great circle (curved) that goes between Australia, Baja California, Long Island, and Sweden.

Then, he states that two planes disappeared within three hours of one another, one over Baja and one over Sweden. He claims these are on opposite sides of the Earth, although they are 10,000 km or a quarter of a circumference apart. Anyway, he uses this to conclude that the orbital period of the satellite must be six hours. Those of you familiar with the ISS know that it is 400 kilometers up and orbits in about 90 minutes. Those of you also familiar with orbital dynamics know that a more distant orbit takes longer, so you could conclude that the moon should be higher up than the ISS. You can use Kepler’s or Newton’s Laws to figure out how high a six-hour orbit around the Earth would be:

$$T^2=(R+h)^3\frac{4\pi}{GM}$$

This should be about 18,000 km if my calculations are correct. In the story, all the planes disappear when trying to break the altitude record, and this happens at forty miles (70 km) altitude. A slight underestimate given the predicted orbital period, but fortunate for the story.

How would this planet look from Earth? In the story, a character asks how this moon could exist if nobody has ever seen it. The protagonist suggests that it must be moving so fast that nobody would ever manage to glimpse it, like the bullet from a rifle. Let’s see if this holds up. First of all, we can calculate the speed based on the height and period, it’s just 2$\pi$ (6380 km + 40 miles)/6 hours=1.8 km/s. I believe this is the speed of a fast bullet but is much slower than the actual orbital velocity of something at that height (around 8 km/s).

When the protagonists are on the satellite and are captured by the frog vampires, somebody mentions “Our little world is but a tenth or less the size of your great Earth which it circles.” Let’s assume that this refers to the radius or diameter so that it has 1% of the area of the Earth (about half the size of Canada) and 0.1% of the volume. This gives it a diameter of 1274 km, about a third that of the moon. So already, you have something that is 36% as wide as the moon but that is about 1/60th the distance. You can imagine it would look pretty large it would take up the entire sky when overhead, and about 11 degrees (20 times the width of the sun and the moon) when viewed from the center of the Earth. The sun and moon appear to cover their distance in about four minutes, whereas this would take about twelve minutes to completely pass overhead. I feel like people would notice that. Probably for the sake of narration, we should take that “a tenth or less” bit quite liberally.

The orbital arrangement in the story.

What about gravity on this moon? In the story, they are described as being able to jump very high  (“But unheeding in their eagerness this strange effect of the satellite’s lesser gravitational power, they moved on, each step a giant, clumsy leap. “) and are super strong (“Norman, though, was relying on the fact that on the second satellite, with its far lesser gravitational influence, their Earth-muscles gave them enormous strength. “). If it has a similar composition as the Earth, it wouldn’t necessarily have the same density, because the Earth’s mass compresses material in its interior (this is called Central Condensation), it would probably have a similar density as the moon, which is about 60% that of Earth’s (about 3.3 kg/L). Applying Newton’s law to find the gravitational field, we find that this is about 1/166 of Earth’s gravity. They’d be more than able to jump, they’d be able to fly. However, the escape velocity is still over 800 m/s, and according to Randall Monroe’s gravity well height calculator it would be about 38 km deep…coincidentally almost reaching the Earth. It would likely not have a bound atmosphere as it does in the story.

What gravitational effects would this have on the Earth? Well, having an object with a thousandth of its mass just beyond its surface would shift the center of mass of the Earth-satellite system to about a thousandth of its radius, about 6 km, so there’s no risk of the surfaces touching. The main effect, I imagine, would be the tides. In a previous article, I mentioned that tidal forces, arising from the gravitational field gradient across an object, scale with the inverse cube instead of the inverse square of the distance. That is why the moon’s tidal influence on the Earth is twice as strong as the sun’s. Let’s calculate the influence that this second satellite would have:

$$\Delta g = \frac{GM}{R^2}-\frac{GM}{(R+L)^2}\approx 2\frac{GM}{R^3}L$$

With L in this case being the diameter of the Earth. For the moon’s influence, we have about $2×10^{-6}$ m/s/s. For the moon in the story, the tidal field is about 0.01 m/s/s, or 5,000 times that of the moon (although my long-distance approximation here might not be valid). It wouldn’t just cause high tides, it would obliterate the planet. The Earth would have a similarly obliterating effect on the moon. Hamilton made this moon way, way too big.

According to an unsourced line on his Wikipedia page, Hamilton was quite a smart guy, entering university at age 14 but dropping out at 17. If I were to hazard a guess, I’d say he just made up numbers as he went along without too much concern for their technical accuracy, trying to write a fanciful story. The story itself, what I’ve heard of it so far, isn’t terrible, although it’s not especially great.

There is a lot of good science fiction out there where you can tell the authors have done a lot of homework getting the technical details right. Neal Stephenson and Greg Egan are examples that come to mind. One could imagine basing a homework assignment on some of the orbital dynamics that arise in Stephenson’s Seveneves, for example. However, it can also be fun and educational to just pick apart something that is not right, as we’ve done here.