Addressing the “Classical Physics Is Wrong” Fallacy
One of the common questions or comments we get on PF is the claim that classical physics or classical mechanics (i.e. Newton’s laws, etc.) is wrong because it has been superseded by Special Relativity (SR) and General Relativity (GR), and/or Quantum Mechanics (QM). Such claims are typically made by either a student who barely learned anything about physics or by someone who has not had a formal education in physics. There is somehow a notion that SR, GR, and QM have shown that classical physics is wrong, and so, it shouldn’t be used.
There is a need to debunk that idea, and it needs to be done in the clearest possible manner. This is because the misunderstanding that results in such an erroneous conclusion is not just simply due to lack of knowledge of physics, but rather due to something more inherent in the difference between science and our everyday world/practices. It is rooted in how people accept certain things and not being able to see how certain ideas can merge into something else under different circumstances.
Before we deal with specific examples, let’s get one FACT to straighten out:
Classical physics is used in an overwhelming majority of situations in our lives. Your houses, buildings, bridges, airplanes, and physical structures were built using the classical laws. The heat engines, motors, etc. were designed based on classical thermodynamics laws. And your radio reception, antennae, TV transmitters, wi-fi signals, etc. are all based on the classical electromagnetic description.
These are all FACTS, not a matter of opinion. You are welcome to check for yourself and see how many of these were done using SR, GR, or QM. Most, if not all, of these, would endanger your life and the lives of your loved ones if they were not designed or described accurately. So how can one claim that classical physics is wrong, or incorrect, if they work, and work so well in such situations?
What actually is true is that we discovered a more accurate, and more general description of our world. In this description, it turns out that classical physics appears as a “simplification” or “approximation” whereby it becomes more and more valid as various parameters approach the common, everyday, terrestrial values. And this is an extremely important point to remember because since classical physics works under our ordinary situation, any new theory or description must somehow converge and look like the classical physics description under such ordinary conditions. Otherwise, this new theory must show that it produces the same set of results as classical physics for all of our known phenomena that classical physics can already accurately described.
So in this part of the article, I will show two specific examples where the more general theory of SR and QM merge smoothly into the classical physics form when one adopts the appropriate approximation. This means that at some limit, both SR and QM descriptions will be the same as the classical description.
Table of Contents
Example 1: Special Relativity Velocity Addition
The first example is from SR and deals with the velocity addition in different inertial reference frames. This is illustrated in the figure below:

The reference frame S’ is moving with velocity v with respect to reference frame S. A vessel is moving with velocity v’ with respect to S’ frame. What is u, the velocity of that vessel with respect to frame S?
The “normal” way to find this velocity is using what is known as Galilean transformation. Here, since both v and v’ and in the same direction, the velocity of the vessel with respect to S frame is a simple addition, i.e.
u = v + v’ (1)
Keep that result in mind.
Now let’s look at how we do this in SR, which is the more general description of such kinematics. Here, we use what is known as the Lorentz transformation. Using the figure from above as before, the velocity u of the vessel in S frame is:
 (2)
(2)
where c is the speed of light in a vacuum.
Now, this looks different than the Galilean transformation that we are used to in Eq. 1. This works for reference frame S’ at any velocity v, even if it approaches c. At that value, Eq. 1 does not work, and the velocity addition that we are used to fails miserably.
However, what happens when v«c, i.e. when reference frame S’ moves much slower than the speed of light? This is what we normally encounter, i.e. someone moving in a vehicle or an airplane. For v«c, Eq. 2 simplifies quite a bit. Without having to do any kind of Taylor series expansion on the denominator of Eq. 2, we can already see that the ratio vv’/c^2 « 1, i.e. it is a very small fraction less than one (v’ cannot be greater than c). This means that, to a good approximation, the denominator of Eq. 2 is essentially just 1.
When that happens, Eq. 2 then simplifies to u = v + v’, which is exactly Eq. 1! We got back our familiar result when we apply the more general equation (Eq. 2) to our normal, terrestrial condition! This means that all of the velocity addition equations and concepts that we already know using Galilean transformation are derivable from the more general Lorentz transformation equations. The Lorentz transformation is the more accurate, more encompassing description of velocity addition, while the Galilean transformation, which is what we know and are familiar with, is simply a special case for when the other reference frame is moving much slower than the speed of light. Eq. 1 isn’t wrong. It has a limited range of situations when it is valid or accurate enough.
Example 2: Quantum Mechanics Rate of Change of Momentum
In classical Newtonian mechanics, for an object with mass m, we know about Newton’s Second Law that relates the force F and the resulting acceleration a, which is
F = ma
This familiar equation can actually be written in a more general form, which is in terms of the time rate of change of momentum p, i.e.
F = dp/dt (3)
We also know that force F can be related to the potential energy (V) gradient, i.e.
F = – dV/dx (in 1D) (4)
So that is from the classical mechanics’ side. Let’s look at what it says on the QM side. Here, we use the Ehrenfest theorem, which says:
 (5)
(5)
Here, H is the Hamiltonian, Q is an operator representing any observable, the square bracket represents the commutator, while the angled bracket represents the average value. These are all the standard notations used in QM.
So what if we want to find the time rate of change of the momentum, p? In QM, p is an operator representing the observable momentum. Thus, Eq. 5 becomes
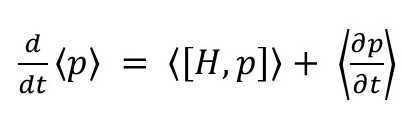 (6)
(6)
From here, it requires quite a bit of knowledge on how to perform the commutator and take the average. You may read the full derivation of it here. In the end, what you end up with is:
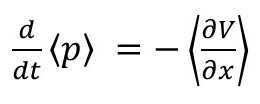 (7)
(7)
This says that the time rate of change of the average value of the momentum p is equal to the average of the gradient of the potential energy V. But this equation is equivalent to Eq. 3 and 4 from classical mechanics! They have identical forms!
It says that what we typically measure in our everyday lives are really the “average” values of many, many, many values at the QM level. The QM description has made the connection to the classical description under the condition that the QM observables have been averaged. Again, as in the case of velocity addition, we get back the classical description from a more general starting point, in this case, a QM description, upon applying a particular condition to the QM picture. It shows that the classical picture is not wrong. It is the average over a large number of QM observables.
Moral of the Story
- Classical physics WORKS for our ordinary situation, so it HAS to be valid at some level.
- Classical physics has been shown to be derivable from SR and QM under special conditions that apply to our ordinary situation.
- Any theory MUST have the ability to show that it merges to the classical description when applied to an ordinary situation.
- This can only be shown mathematically. It cannot be shown convincingly via hand-waving or qualitative arguments. It is the equivalent mathematical form that shows that one theory can derive the other.
What this implies here is that, if there are more general and more accurate theories beyond QM, SR/GR, then those theories must also show that they can be “simplified” into the mathematical forms of QM and SR/GR. Subsequent, more general theories must show that they can derive the mathematical forms of existing, already-working theories. The inability to do that will be a fatal flaw in any new theory.
I mentioned towards the beginning of this article that the inability to comprehend this concept of a more general idea merging and agreeing with something less general may have something to do with the differences between science and our everyday lives. It is unusual for many people to accept the possibility that a simplistic, less sophisticated, and apparently different idea is actually a subset of a more general principle. The fact that one can actually start with a more general principle, apply certain criteria, and then get a seemingly different concept, is not something a lot of people are familiar with, or would even accept.
It is why for someone not trained in physics, the idea that classical mechanics can actually be derived from seemingly a different animal of QM or SR/GR would not even cross his/her mind. Yet, in science/physics, this is quite common. We always show how new ideas and theories will turn into the old, tested, and well-known ideas and theories under the appropriate parameters. It is very seldom that old theories are discarded wholesale.
PhD Physics
Accelerator physics, photocathodes, field-enhancement. tunneling spectroscopy, superconductivity








It is not part of the theory (as initially proposed by Newton) that the theory is only intended to apply up to a certain limit.Of course not, the Newtonian limit is part of relativity and QM, not part of Newtonian mechanics. I have read the context and your statements repeatedly show this misunderstanding.
The second and much more minor point is that Newton is not the final authority on what Newtonian mechanics is. It is named after him because he started it, but its development continued long after him. He started it, not finished it. Many things that we recognize today as being parts of Newtonian mechanics were from the work of others, not Newton.Indeed – Dirac had an interesting view on this (we don't discuss philosophy here but I cant resist – Kuhn – watch out):
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.485.9188&rep=rep1&type=pdf
Thanks
Bill
I am glad that we now agree. Although if you agree with my first paragraph then I cannot see how you could claim that it is “happenstance”Like a lot of things in this thread it has to be read in context but basically what I was saying was that the fact that Newton's theories (as originally proposed by Newton) make predictions which are approximately accurate only up to a certain limit is a "happenstance". It is not part of the theory (as initially proposed by Newton) that the theory is only intended to apply up to a certain limit.
But the start of your article is, I think, more polemical and you are exaggerating to redress the opposite extreme of how you perceive "people who have asked on this forum think"And like I said, that is now a matter of semantics and personal preference. I stated that based on many years of observations of members here in this forum when we repeatedly dealt with such topics.
Zz.
I agree with everything you say (except your first sentence!) and that is exactly my point.I am glad that we now agree. Although if you agree with my first paragraph then I cannot see how you could claim that it is “happenstance”
Unfortunately, this is now semantics. But this is not how people who have asked this on this forum think, because they are under the impression that we should NOT be using Newton's laws, under ANY limits, because it has been shown to be "wrong" by QM and SR/GR. THAT is the argument that I'm countering against.
Zz.I think you make that point very well here:
"Moral of the Story
Classical physics WORKS for our ordinary situation, so it HAS to be valid at some level.
Classical physics has been shown to be derivable from SR and QM under special conditions that apply to our ordinary situation.
Any theory MUST have the ability to show that it merges to the classical description when applied to ordinary situation."
For each of the three points you are careful to stress the limits ("at some level", "our ordinary situation", "to ordinary situation")
But the start of your article is, I think, more polemical and you are exaggerating to redress the opposite extreme of how you perceive "people who have asked on this forum think"
Exactly, but I’m not sure this point comes out clearly in your article. To say that
1. Newton was wrong (about a lot of things)
is not incompatible with saying that
2. It just so happens that within certain limits (which limits we now are aware of and he wasn’t) parts of his theory are mathematically correct to a very good approximation and very useful in fields of engineering."no incompatible" means "compatible"?
If that is so, then I do NOT seem those two as being compatible. To say that Newton's laws are wrong, and then to turn around and use it, is an inconsistent act.
To say that it is accurate over a certain limit, and then to turn around and use it within those limits, is NOT an inconsistent act.
Unfortunately, this is now semantics. But this is not how people who have asked this on this forum think, because they are under the impression that we should NOT be using Newton's laws, under ANY limits, because it has been shown to be "wrong" by QM and SR/GR. THAT is the argument that I'm countering against.
Zz.
-"Classical physics is used in an overwhelming majority of situations in our lives." so what? do examples prove that a theory is correct?No it doesn't – nothing can prove any theory correct and classical mechanics is no exception. All theories are just provisional.
But I think before forming an opinion you need to read Landau – Mechanics.
It is based on the principle of least action which must be true if QM is true providing you are dealing with the regime such that close paths cancel – only stationary paths do not cancel – they reinforce – this is from Feynman's path integral approach which is logically equivalent to usual QM. In Landau, assuming just that and symmetry you basically get classical mechanics. Does that make classical mechanics correct – of course not – but if its wrong then we have a rot in QM and that would be very revolutionary indeed. In fact we have reason to believe QM at levels we can currently reach would be unlikely to be wrong:
https://arxiv.org/pdf/quant-ph/0401062.pdf
Again QM is just provisional, like any theory – but what Wienberg's paper shows is if it is wrong there is something basically wrong with some very fundamental things we think is true about our world – so fundamental it should have been picked up by now – but doubt is one of the essential basics of science so one never knows – it just if this is wrong it would be very very revolutionary.
Thsnks
Bill
You are missing two points. The first and most important is that the Newtonian limit is not a feature of Newtonian mechanics, it is a feature of subsequent theories. The Newtonian limit does not belong to Newtonian mechanics, it belongs to relativity and it belongs to QM. If those two theories did not possess a Newtonian limit then they would be wrong. The existence of a Newtonian limit for relativity and QM is not a necessary condition for Newtonian physics to be right, it is a necessary condition for QM and relativity to be right. It is certainly not happenstance since the founders of relativity and QM worked hard to include a Newtonian limit in their theories since they recognized the necessity.
The second and much more minor point is that Newton is not the final authority on what Newtonian mechanics is. It is named after him because he started it, but its development continued long after him. He started it not finished it. Many things that we recognize today as being part of Newtonian mechanics was from the work of others, not Newton.I agree with everything you say (except your first sentence!) and that is exactly my point. Most of the controversy arises because people are using the phrases “Newtonian Mechanics” and “Classical Physics” with different understood meanings without declaring what definition they are using.
’m just querying your use of the words “Newtonian limit”. This is a modern concept, not one that Newton recognised.You are missing two points. The first and most important is that the Newtonian limit is not a feature of Newtonian mechanics; it is a feature of subsequent theories. The Newtonian limit does not belong to Newtonian mechanics; it belongs to relativity and it belongs to QM. If those two theories did not possess a Newtonian limit then they would be wrong. The existence of a Newtonian limit for relativity and QM is not a necessary condition for Newtonian physics to be right; it is a necessary condition for QM and relativity to be right. It is certainly not happenstance since the founders of relativity and QM worked hard to include a Newtonian limit in their theories; they recognized the necessity.
The second and much more minor point is that Newton is not the final authority on what Newtonian mechanics is. It is named after him because he started it, but its development continued long after him. He started it, not finished it. Many things that we recognize today as being parts of Newtonian mechanics were from the work of others, not Newton.
I am not sure what you mean. In the limit v<<c and weak gravity we recover Newton’s three laws and his law of gravitation. What more is there?Newton did not regard his theory as limited to v<<c and did not regard his theory as limited to weak gravity.
I’m just querying your use of the words “Newtonian limit”. This is a modern concept, not one that Newton recognised.
I think a lot of the controversy about whether Classical physics is “wrong” is caused by different people using the same words with different meanings.
One group means by Classical Physics “that part of (or those circumstances in which) Newton’s theory produces predictions which we now know to be still approximately correct” – this group is outraged by the idea that anyone should seem to write off Classical Physics as simply “wrong”
The other group means by Classical Physics “Newton’s theories taken as a whole” – this group can’t understand why the other group is so outraged by any suggestion that Newton’s theories may not be wholly correct.
Each group can be tempted to exaggerate its position in order to try to redress the balance!
I think you are unconsciously using (as many people do) the words “Newtonian limit” to mean the whole of Newton’s theories. But it is only a subset of Newton which approximately corresponds to a subset of relativity.I am not sure what you mean. In the limit v<<c and weak gravity we recover Newton’s three laws and his law of gravitation. What more is there?
No, it is not happenstance. It is a necessary condition for future theories to be considered valid. To be valid, both relativity and QM must unavoidably have a Newtonian limit. Not as a matter of coincidence but precisely because Newtonian physics has a large body of experimental validation.
If they did not have a Newtonian limit then they would have been immediately discarded. They would have been falsified by all of the experiments that validate Newtonian physics.I think you are unconsciously using (as many people do) the words “Newtonian limit” to mean the whole of Newton’s theories. But it is only a subset of Newton which approximately corresponds to a subset of relativity. The boundary of the subset of Newton’s theory is a happenstance conditioned by the limits of the experimental opportunities he happened to have available to him.
Ultimately it is a happenstance.No, it is not happenstance. It is a necessary condition for future theories to be considered valid. To be valid, both relativity and QM must unavoidably have a Newtonian limit. Not as a matter of coincidence but precisely because Newtonian physics has a large body of experimental validation.
If they did not have a Newtonian limit then they would have been immediately discarded. They would have been falsified by all of the experiments that validate Newtonian physics.
The aim of a theory in empirical science is not to be "mathematically correct" and it is unclear what you would even mean by something like that. What matters is if the theory makes correct predictions or not.
.Yes, by mathematically correct I meant approximately correct predictions in terms of *measurement*. Not in the sense of getting your sums right!
Measurement is not all of Physics. There are also concepts. Newton’s predictions for the effects of gravity may be approximately correct in terms of measurement in certain circumstances, but GR regards his idea of gravity being a force as incorrect (in all circumstances).
you are defining “classical limit” as meaning “that part of Newton’s theory which is approximately mathematically correct”The aim of a theory in empirical science is not to be "mathematically correct" and it is unclear what you would even mean by something like that. What matters is if the theory makes correct predictions or not.
Also, "approximately" and "mathematically correct" would typically not be two words that mathematicians would like to string together in a sentence. That 2 = 2.000123 is not approximately mathematically correct, it is wrong.
It doesn't "just so happen". It's a necessary feature of any theory that it looks like Newton in the classical limit because the real world looks like Newton in the classical limit. If it doesn't look like Newton it doesn't look like the real world.It is only *necessary* in the weak sense that you are defining “classical limit” as meaning “that part of Newton’s theory which is approximately mathematically correct”. It is necessary only because of your definitions. Ultimately it is a happenstance.
It just so happens that within certain limitsIt doesn't "just so happen". It's a necessary feature of any theory that it looks like Newton in the classical limit because the real world looks like Newton in the classical limit. If it doesn't look like Newton it doesn't look like the real world.
parts of his theory are mathematically correct to a very good approximation and very useful in fields of engineering.But that's true of relativity and quantum too. And we will always have to suspect that any future theory may be invalid outside the regime we have tested. So we can describe every theory as wrong and regard it as mere coincidence that it works. Or we can take @Orodruin's point that a theory is better regarded as its testable predictions, not its untestable assumptions, and regard it as right when those predictions are accurate to available precision.
That’s because he didn’t know any better. WE now know the limits where it is valid.
Zz.Exactly, but I’m not sure this point comes out clearly in your article. To say that
1. Newton was wrong (about a lot of things)
is not incompatible with saying that
2. It just so happens that within certain limits (which limits we now are aware of and he wasn’t) parts of his theory are mathematically correct to a very good approximation and very useful in fields of engineering.
I have a warning to all future Einsteins: Make sure you explain what we already know (which is now quite a lot) and your new theory recover ours in some limiting case.Something all serious physicists do, but nearly no crackpot even tries. Typically because the crackpots don't even know what is known.
He, he, I was a high school kid when entertained in such an obvious topic. Of course Newton was and is perfectly correct in its sphere of applicability, of low velocities and week gravitational fields. Take a limit of all SR formulas as c goes to infinity and you recover the clasical mechanics. Set Planks constant to zero and same for QM. I have a warning to all future Einsteins: Make sure you explain what we already know (which is now quite a lot) and your new theory recover ours in some limiting case. Good luck!
By 'classical limit' do you mean the slow speeds for which we now regard classic physics as providing a good approximation? If so that appears to be a modern definition of 'classical'. Newton, for example, did not regard his theories as so limited.That’s because he didn’t know any better. WE now know the limits where it is valid.
This is true for anything. We now know more than before on a lot of things.
Zz.
Obviously you will not recover classical mechanics in the ultra-relativistic limit, you will recover it in the classical limit where speeds are much smaller than the speed of light.By 'classical limit' do you mean the slow speeds for which we now regard classic physics as providing a good approximation? If so that appears to be a modern definition of 'classical'. Newton, for example, did not regard his theories as so limited.
I'm a bit puzzled by this discussion too. It is indeed true that most results of engineering are using classical physics to construct machines etc. making our lifes convenient. Obviously classical physics (i.e., all physics, including relativity, which is not using quantum theory) works very well in its range of applicability. This is ensured by the empirical method, i.e., that theoretical claims have to be tested in experiments and careful quantitative observations of Nature.
It is of course clear that any application of, e.g., classical electrodynamics uses relativity since classical electrodynamics is a relativistic classical field theory. The matter is treated phenomenologically in terms of continuum mechanics (entering the Maxwell equations in terms of charge-current densities) and using some phenomenological "transport coefficients" like electric conductivity, electric permittivity, and magnetic permeability.
Another question is, why this works so well, given the fact that indeed the most fundamental theory is Q(F)T. The answer is that in everyday-life we encounter macroscopic situations, where we don't need to describe the relevant degrees of freedom microscopically, which is not even possible because we cannot handle the about ##10^{24}## degrees of freedom of one mole matter anyway. The relevant degrees of freedom are the usually slowly varying collective observables like the center of mass (momentum) of a body or the thermodynamically averaged electromagnetic charge-current-magnetization distributions of matter and quantities like this. The usual constitutive phenomenological laws of electromagnetism, all involving transport coefficients that can be derived from quantum-many-body theory and the appropriate coarse-grained approximations leading to Boltzmann/BUU equations or viscous (or even ideal) (magneto-)hydrodynamics, are derived from linear-response theory or, if necessary, beyond.
This indeed implies that there is no contradiction between the fact that in many everyday situations classical physics is an excellent effective description of what's going on and it can very successfully be used in engineering.
If I say that the assumptions are: time is relative and space is Riemaniann and you say: time is absolute and space is euclidian, how can we be talking about the same theory?By working the math. A lot of things that we may verbally or philosophically consider different are mathematically equivalent. You may think that you are drawing an important distinction between Newtonian and Relativistic mechanics, but in the v<<c limit this distinction is only in your mind and does not appear in either the math or experiment.
A theory is not its underlying assumptions – which can never be tested, it is its predictions.Some fundamental assumptions of classical physics have been called into question by experimental observations.
First of all, it was MY article..Oops. Sorry for that. I will read it again! I confused the avatars!
I don't know how we separate assumptions from predictions. If I say that space-time is an entity and can be distorted, if we can't find a way to test it, the theory won't last. In my point of view the assumptions will direct affect what we are going to observe.You cannot "measure" spacetime. You can make prediction of the consequences of a particular spacetime geometry and then measure those consquences. This is what @Orodruin was referring to.
When I started to discuss your article, my point was: If we want to explain why Newtonian Mechanics is not wrong, why do we need to use the convergence of new theories for that? that's where I do not agree, as I said on previous arguments. it makes no sense to me.First of all, it was MY article.
Secondly, it was written in response to members who claim that Newtonian mechanics is wrong BECAUSE it has been superceeded by QM and SR/GR. Read it again! It was written clearly as the impetus for the article. That is why I made the connection between the two.
Zz.
Physics is an empirical science and what you can test are the predictions of a theory. If two theories make fundamentally different "assumptions" but give rise to the same observables, then there is no way of telling them apart and for empirical purposes the two are identical. You can never test assumptions (unless those assumptions are directly observable – but other assumptions could also lead to those testable assumptions being predictions as well).I don't know how we separate assumptions from predictions. If I say that space-time is an entity and can be distorted, if we can't find a way to test it, the theory won't last. In my point of view the assumptions will direct affect what we are going to observe.
When I started to discuss your article, my point was: If we want to explain why Newtonian Mechanics is not wrong, why do we need to use the convergence of new theories for that? that's where I do not agree, as I said on previous arguments. it makes no sense to me.
Newton had a set of problems and variables to think of, which pushed him towards some thinking pattern. Of course we all know now that he explained the world. Einstein had a different set of problems and the change on the assumptions modified a lot (cosmology and QM) what we know about the universe. The fact that Newtonian Mechanics works on our daily basis establishes only its boudaries of usage. And inside those boundaries, its correct within necessary precision.
Well, that's where we don't agree. I guess we are going nowhere here. anyway, thanks for the chat. I will think about the insights you all gave. see ya.Physics is an empirical science and what you can test are the predictions of a theory. If two theories make fundamentally different "assumptions" but give rise to the same observables, then there is no way of telling them apart and for empirical purposes the two are identical. You can never test assumptions (unless those assumptions are directly observable – but other assumptions could also lead to those testable assumptions being predictions as well).
A theory is not its underlying assumptions – which can never be tested, it is its predictions.Well, that's where we don't agree. I guess we are going nowhere here. anyway, thanks for the chat. I will think about the insights you all gave. see ya.
What difference does it make if you get the old theory from an upper limit or any other arbitrary direction?Uhmmm … Are you serious or just trolling? Obviously it matters that you recover the old theory in the limit where the old theory is known to be applicable or if you do so in the opposite limit.
This does not make any sense. If I say that the assumptions are: time is relative and space is Riemaniann and you say: time is absolute and space is euclidian, how can we be talking about the same theory?We are not. We are only talking about the limit of one of the theories. In the classical limit you do recover the very same things as the classical theory. That SR is applicable to a larger set of situations is not the issue here.
No, you are wrong. What I said was that the assumptions are different! If you look at how we treat all the experiments and particles / waves in quantum world, we see that space, time, energy e whatever are all different from what we knew from classical mechanics, which means, we cannot start to say that there exists a derivation from one to another, as they were talking, ever, about the same thing.This is just wrong. As already illustrated in the actual Insight. You can start from different assumptions, but in the end what it boils down to is to make identifications of what concepts in a theory that correspond to the concepts of the previous. A theory is not its underlying assumptions – which can never be tested, it is its predictions.
I'm talking about how do we explain an theory evolution without wanting to find convergencies that were created just to make understanding easier.I am sorry but you are not making any sense here. The point is that the "old" theory typically has made a large number of verified predictions that are well studied enough that we know how experiments behave in a certain range – at least to within experimental uncertainty. Under the same type of conditions, the "new" theory must therefore reproduce exactly the same results up to corrections that are smaller than the experimental uncertainty. This is what it means having the "old" theory as a limiting behaviour. It has absolutely nothing to do with what "basic assumptions" have been made, just about predictions.
I am not saying that Newtonian Mechanics is wrong. this has nothing to do with being right or wrong.Actually, it does! That's the whole point of my writing the article, that we frequently have members here claiming that Newtonian mechanics is wrong, and questioned why we continue to use it! If you make no such claim, then the article wasn't meant for you.
You also read WAY too much philosophical implication to what the article had said. First of all, I never said anything about any "proofs" that one theory equals the other. All I did was show that, in certain limits or situation, one theory can reproduce the mathematical form of the other. None of what I had shown should be a surprise, because we all saw this in undergraduate physics courses!
Furthermore, we do not have to go to wide extreme to see this. Even within classical mechanics itself, the Newtonian mechanics and the Hamiltonian/Lagrangian mechanics already have philosophically different approach and "world view". And yet, they both arrive at the same mathematical form in describing the kinematics of a system.
Being able to show that something can be derived into a familiar form is a powerful and extremely useful argument. This is done in mathematics all the time. The ability to reformulate a differential equation into something that we know the solution of is done often. So it is no different here in physics. It says that the new idea can reproduce all of the results of the old ideas, and also shows why and where the old ideas may fail or no longer accurate enough.
Zz.
I am sorry, but this is just ignorant and the limit is not arbitrary. Obviously you will not recover classical mechanics in the ultra-relativistic limit, you will recover it in the classical limit where speeds are much smaller than the speed of light.What difference does it make if you get the old theory from an upper limit or any other arbitrary direction? My point was that SR is considering space and time as completly different things comparing to old mechanics. This does not make any sense. If I say that the assumptions are: time is relative and space is Riemaniann and you say: time is absolute and space is euclidian, how can we be talking about the same theory?
When it comes to light it is very well explained using Maxwell's theory. When it comes to particles such as electrons, it is not a prediction of the classical theory but your logic is completely flawed. You have taken one of the shortcomings of the classical theory that inspired people to QM and presented it as a counter argument to the quantum theory having to reduce to the classical theory in the limits where we know that the classical theory works. We already know that the classical theory does not work in this limit and so your argument is empty. Essentially you argument to the statement "A must give the same predictions as B when C is true" is to say "but it does not give the same predictions when C is not true". We come back to your assertion that the limit is arbitrary which, again, is not the case.No, you are wrong. What I said was that the assumptions are different! If you look at how we treat all the experiments and particles / waves in quantum world, we see that space, time, energy e whatever are all different from what we knew from classical mechanics, which means, we cannot start to say that there exists a derivation from one to another, as they were talking, ever, about the same thing. Again, if you start with different assumptions how can you end up with theories converging at a limit that has been chosen to find a connection between them?
I am not saying that Newtonian Mechanics is wrong. this has nothing to do with being right or wrong. I'm talking about how do we explain an theory evolution without wanting to find convergencies that were created just to make understanding easier.
Great article @ZapperZ . I especially liked the part where you talk about the thought processes of the public as compared to physicists (I would use the broader term "technically trained" instead of physicist) .
We usually discourage talk about philosophy here on PF. But in the meaning of the word, "thinking about thought" it goes the heart of your point. I believe that you are correct; that fundamentally different thought processes forever divide the technical and liberal views of our world.
Well obviously Newtonian mechanics is "wrong"Obviously it is not wrong. It has been experimentally verified by a large number of experiments.
People tend to think of experimental falsification as much stronger than experimental verification. But it is not. The fact that a theory later produces incorrect results in some new domain does not change the fact that it does produce correct results in the previous domains.
So “wrong” would be a description for a theory that is never correct in any domain. Other than that theories are “applicable” or not to a given domain, or they are more or less “general” than another theory.
I said that there is no such a thing as a convergence from a new theory to an old one based on some arbitrary limitI am sorry, but this is just ignorant and the limit is not arbitrary. Obviously you will not recover classical mechanics in the ultra-relativistic limit, you will recover it in the classical limit where speeds are much smaller than the speed of light.
In physics and any empirical science, a theory is nothing else than the sum of its predictions. This is why discussions on quantum mechanics interpretations tend to degenerate and people either leaving upset or agreeing to disagree.
Apart from that:
– Newton considered space as an R³ euclidean and time as absolute.
– Mass and energy were not connected the way we know now.The first of these follows directly in the classical limit of SR. The second also falls out of the theory as separate conservation of mass and kinetic energy at small velocities.
– How would we explain the double slit experiment?When it comes to light it is very well explained using Maxwell's theory. When it comes to particles such as electrons, it is not a prediction of the classical theory but your logic is completely flawed. You have taken one of the shortcomings of the classical theory that inspired people to QM and presented it as a counter argument to the quantum theory having to reduce to the classical theory in the limits where we know that the classical theory works. We already know that the classical theory does not work in this limit and so your argument is empty. Essentially you argument to the statement "A must give the same predictions as B when C is true" is to say "but it does not give the same predictions when C is not true". We come back to your assertion that the limit is arbitrary which, again, is not the case.
Well obviously Newtonian mechanics is "wrong" since it does include relativity or quantum mechanics but that does not imply that it "shouldn't be used". Newtonian mechanics is "wrong" in the sense that it is not the real Universe but that does not imply that it is wrong for you to use it because usually the error intrinsic to Newtonian mechanics is small enough that you can safely ignore it.
@ZapperZ great article! This is why, more than 100 years after Einstein, students still learn Newton. I have had discussions with people who are convinced that because Einstein proved Newton wrong someone will eventually prove Einstein wrong. But future generations of students will still need to learn relativity even if a Lorentz violating theory is eventually verified.
Thank you for an enjoyable, edifying read.
do examples prove that a theory is correct?Obtaining examples where a theory works or doesn’t work is the whole purpose of experiments in the scientific method. We don’t usually use the word “prove”, but examples do verify or falsify theories.
In Helen Quinn's essay in Physics Today, she emphasized the same issue:
We also know that they are not complete. Although they are well tested in some domains, in others uncertainties remain about their detailed application. Indeed, we expect that they will be modified or extended to explain new evidence. But they will not disappear; just as Newton's laws did not become invalid when we understood special relativity, but rather were seen to be a very accurate approximation under well-defined conditions. Theories such as those listed in the previous paragraph are strong enough that we can use them to say we know certain things – we know that protons and neutrons are composed of quarks and gluons, we know the relationship between mass and energy, we know that Earth's surface is not a single rigid structure. These are facts, but not just simple observational facts. They come from the amalgam of observation and theory development and testing that is the essence of scientific knowledge development. It diminishes the status of our understanding greatly to say that scientists "believe" these things. We know them!
When we seek to extend and revise our theoretical frameworks, we make hypotheses, build models, and construct untested, alternate, extended theories. These last must incorporate all the well-established elements of prior theories. Experiment not only tests the new hypotheses; any unexplained result both requires and constrains new speculative theory building – new hypotheses. Models, and in the modern world computer simulations too, play an important tole here. They allow us to investigate and formulate the predictions and tests of our theory in complex situations. Our hypotheses are informed guesses, incorporating much that we know. They may or may not pan out, but they are motivated by some aspects or puzzles in the existing data and theory. We actively look for contradictions.There is an under-emphasis of the significance and importance of the claim that "it works!". Nothing is more powerful than having experimental evidence, and having it being verified and used every single day. Sure, as an experimentalist, I am probably very bias towards experimental evidence. However, this is what clearly separates science from non-science, and what makes acceptance in physics extremely difficult due to the requirement of having clear and convincing empirical evidence.
Zz.
I never said that Newtonian mechanics was wrong. never said that. I said that there is no such a thing as a convergence from a new theory to an old one based on some arbitrary limit as they start from different assumptions.So your objection is to the term "convergence", taken as an indication that the new theory must, in the appropriate limit, be precisely identical to the old theory and not merely identical to within current experimental uncertainties.
Yes, that is certainly true. [Though precise agreement in the limit is what we have come to expect]
I think you are rather missing the point. If you are travelling at 30mph down the road and a car passes you going 30mph faster, you can calculate its road speed using Newtonian or Einsteinian relativity. You will get the same answer to the precision you can plausibly measure. You need to take into account the velocity variation from flies crashing into the front of the car long before you need to care about Einstein. So simplifying the maths and using Newton isn't wrong. How can it be? Unless you're saying it's wrong to neglect the flies. And if you believe that then you will get nothing done ever.I never said that Newtonian mechanics was wrong. never said that. I said that there is no such a thing as a convergence from a new theory to an old one based on some arbitrary limit as they start from different assumptions.
It does not matter if you derivade classical physics from modern theories, they have different assumptions! they do not talk about the same thing!I think you are rather missing the point. If you are travelling at 30mph down the road and a car passes you going 30mph faster, you can calculate its road speed using Newtonian or Einsteinian relativity. You will get the same answer to the precision you can plausibly measure. You need to take into account the velocity variation from flies crashing into the front of the car long before you need to care about Einstein. So simplifying the maths and using Newton isn't wrong. How can it be? Unless you're saying it's wrong to neglect the flies. And if you believe that then you will get nothing done ever.
If a new theory does not produce approximately same answers as the classical theory in the realm where the classical theory has been tested experimentally and demonstrated to be accurate then that new theory must not be correct.
Experiment is the final arbiter of correctness.Of course the new theory will have to explain the old stuff, but it does not mean that it will "converge" at some point to the old one. there is no connection between the two things.
Apart from that:
– Newton considered space as an R³ euclidean and time as absolute.
– Mass and energy were not connected the way we know now.
– How would we explain the double slit experiment?
The assumptions can't be ignored.
Another great Insight, thanks Zapperz!
– "any new theory or description must somehow converge and look like the classical physics description under such ordinary conditions.". Who said this "must" be true?If a new theory does not produce approximately same answers as the classical theory in the realm where the classical theory has been tested experimentally and demonstrated to be accurate than that new theory must not be correct.
Experiment is the final arbiter of correctness.
– "Classical physics is used in an overwhelming majority of situations in our lives." so what? do examples prove that a theory is correct? this argument makes no sense at all.
– "any new theory or description must somehow converge and look like the classical physics description under such ordinary conditions.". Who said this "must" be true? The point here is that SR and QM deal with different concepts of reality which are not accounted in classical mechanics. We are looking at the old theories with our "present" eyes. We can't interpret the past this way. The assumptions are totally diferent.
– "They have identical form!". Again: having the identical equation form proves what? that they have the same assumptions? that they work on the same space with the same properties? of course not!
It does not matter if you derivade classical physics from modern theories, they have different assumptions! they do not talk about the same thing!
Definitely worth saying. Asimov wrote an article in a similar vein (tip o' the hat to @Nugatory for introducing me to it): http://chem.tufts.edu/answersinscience/relativityofwrong.htm