Addressing the “Classical Physics Is Wrong” Fallacy
One of the common questions or comments we get on PF is the claim that classical physics or classical mechanics (i.e. Newton’s laws, etc.) is wrong because it has been superseded by Special Relativity (SR) and General Relativity (GR), and/or Quantum Mechanics (QM). Such claims are typically made by either a student who barely learned anything about physics or by someone who has not had a formal education in physics. There is somehow a notion that SR, GR, and QM have shown that classical physics is wrong, and so, it shouldn’t be used.
There is a need to debunk that idea, and it needs to be done in the clearest possible manner. This is because the misunderstanding that results in such an erroneous conclusion is not just simply due to lack of knowledge of physics, but rather due to something more inherent in the difference between science and our everyday world/practices. It is rooted in how people accept certain things and not being able to see how certain ideas can merge into something else under different circumstances.
Before we deal with specific examples, let’s get one FACT to straighten out:
Classical physics is used in an overwhelming majority of situations in our lives. Your houses, buildings, bridges, airplanes, and physical structures were built using the classical laws. The heat engines, motors, etc. were designed based on classical thermodynamics laws. And your radio reception, antennae, TV transmitters, wi-fi signals, etc. are all based on the classical electromagnetic description.
These are all FACTS, not a matter of opinion. You are welcome to check for yourself and see how many of these were done using SR, GR, or QM. Most, if not all, of these, would endanger your life and the lives of your loved ones if they were not designed or described accurately. So how can one claim that classical physics is wrong, or incorrect, if they work, and work so well in such situations?
What actually is true is that we discovered a more accurate, and more general description of our world. In this description, it turns out that classical physics appears as a “simplification” or “approximation” whereby it becomes more and more valid as various parameters approach the common, everyday, terrestrial values. And this is an extremely important point to remember because since classical physics works under our ordinary situation, any new theory or description must somehow converge and look like the classical physics description under such ordinary conditions. Otherwise, this new theory must show that it produces the same set of results as classical physics for all of our known phenomena that classical physics can already accurately described.
So in this part of the article, I will show two specific examples where the more general theory of SR and QM merge smoothly into the classical physics form when one adopts the appropriate approximation. This means that at some limit, both SR and QM descriptions will be the same as the classical description.
Table of Contents
Example 1: Special Relativity Velocity Addition
The first example is from SR and deals with the velocity addition in different inertial reference frames. This is illustrated in the figure below:
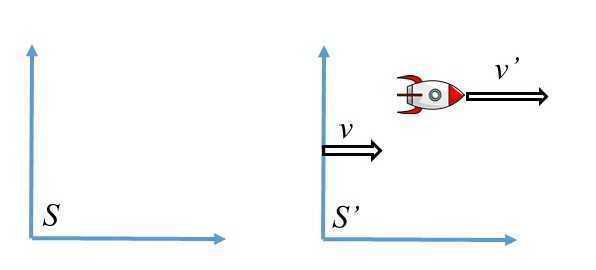
The reference frame S’ is moving with velocity v with respect to reference frame S. A vessel is moving with velocity v’ with respect to S’ frame. What is u, the velocity of that vessel with respect to frame S?
The “normal” way to find this velocity is using what is known as Galilean transformation. Here, since both v and v’ and in the same direction, the velocity of the vessel with respect to S frame is a simple addition, i.e.
u = v + v’ (1)
Keep that result in mind.
Now let’s look at how we do this in SR, which is the more general description of such kinematics. Here, we use what is known as the Lorentz transformation. Using the figure from above as before, the velocity u of the vessel in S frame is:
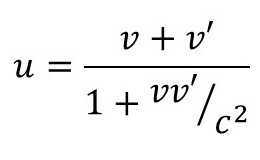 (2)
(2)
where c is the speed of light in a vacuum.
Now, this looks different than the Galilean transformation that we are used to in Eq. 1. This works for reference frame S’ at any velocity v, even if it approaches c. At that value, Eq. 1 does not work, and the velocity addition that we are used to fails miserably.
However, what happens when v«c, i.e. when reference frame S’ moves much slower than the speed of light? This is what we normally encounter, i.e. someone moving in a vehicle or an airplane. For v«c, Eq. 2 simplifies quite a bit. Without having to do any kind of Taylor series expansion on the denominator of Eq. 2, we can already see that the ratio vv’/c^2 « 1, i.e. it is a very small fraction less than one (v’ cannot be greater than c). This means that, to a good approximation, the denominator of Eq. 2 is essentially just 1.
When that happens, Eq. 2 then simplifies to u = v + v’, which is exactly Eq. 1! We got back our familiar result when we apply the more general equation (Eq. 2) to our normal, terrestrial condition! This means that all of the velocity addition equations and concepts that we already know using Galilean transformation are derivable from the more general Lorentz transformation equations. The Lorentz transformation is the more accurate, more encompassing description of velocity addition, while the Galilean transformation, which is what we know and are familiar with, is simply a special case for when the other reference frame is moving much slower than the speed of light. Eq. 1 isn’t wrong. It has a limited range of situations when it is valid or accurate enough.
Example 2: Quantum Mechanics Rate of Change of Momentum
In classical Newtonian mechanics, for an object with mass m, we know about Newton’s Second Law that relates the force F and the resulting acceleration a, which is
F = ma
This familiar equation can actually be written in a more general form, which is in terms of the time rate of change of momentum p, i.e.
F = dp/dt (3)
We also know that force F can be related to the potential energy (V) gradient, i.e.
F = – dV/dx (in 1D) (4)
So that is from the classical mechanics’ side. Let’s look at what it says on the QM side. Here, we use the Ehrenfest theorem, which says:
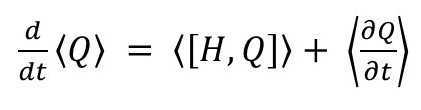 (5)
(5)
Here, H is the Hamiltonian, Q is an operator representing any observable, the square bracket represents the commutator, while the angled bracket represents the average value. These are all the standard notations used in QM.
So what if we want to find the time rate of change of the momentum, p? In QM, p is an operator representing the observable momentum. Thus, Eq. 5 becomes
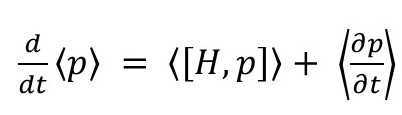 (6)
(6)
From here, it requires quite a bit of knowledge on how to perform the commutator and take the average. You may read the full derivation of it here. In the end, what you end up with is:
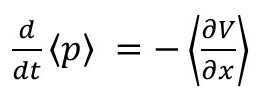 (7)
(7)
This says that the time rate of change of the average value of the momentum p is equal to the average of the gradient of the potential energy V. But this equation is equivalent to Eq. 3 and 4 from classical mechanics! They have identical forms!
It says that what we typically measure in our everyday lives are really the “average” values of many, many, many values at the QM level. The QM description has made the connection to the classical description under the condition that the QM observables have been averaged. Again, as in the case of velocity addition, we get back the classical description from a more general starting point, in this case, a QM description, upon applying a particular condition to the QM picture. It shows that the classical picture is not wrong. It is the average over a large number of QM observables.
Moral of the Story
- Classical physics WORKS for our ordinary situation, so it HAS to be valid at some level.
- Classical physics has been shown to be derivable from SR and QM under special conditions that apply to our ordinary situation.
- Any theory MUST have the ability to show that it merges to the classical description when applied to an ordinary situation.
- This can only be shown mathematically. It cannot be shown convincingly via hand-waving or qualitative arguments. It is the equivalent mathematical form that shows that one theory can derive the other.
What this implies here is that, if there are more general and more accurate theories beyond QM, SR/GR, then those theories must also show that they can be “simplified” into the mathematical forms of QM and SR/GR. Subsequent, more general theories must show that they can derive the mathematical forms of existing, already-working theories. The inability to do that will be a fatal flaw in any new theory.
I mentioned towards the beginning of this article that the inability to comprehend this concept of a more general idea merging and agreeing with something less general may have something to do with the differences between science and our everyday lives. It is unusual for many people to accept the possibility that a simplistic, less sophisticated, and apparently different idea is actually a subset of a more general principle. The fact that one can actually start with a more general principle, apply certain criteria, and then get a seemingly different concept, is not something a lot of people are familiar with, or would even accept.
It is why for someone not trained in physics, the idea that classical mechanics can actually be derived from seemingly a different animal of QM or SR/GR would not even cross his/her mind. Yet, in science/physics, this is quite common. We always show how new ideas and theories will turn into the old, tested, and well-known ideas and theories under the appropriate parameters. It is very seldom that old theories are discarded wholesale.
PhD Physics
Accelerator physics, photocathodes, field-enhancement. tunneling spectroscopy, superconductivity








I would suggest to write another article, reformulating this one in a quite straightforward way, against the
"Flat Earth Theory Is Wrong" Fallacy.
It works, indeed, nicely on the soccer field near my home, and gives accurate predictions for trajectories of the ball.The problem with your logic is as follows:
a) If you use classical physics where it applies (e.g. to build an aircraft), then classical physics is not wrong in that sense.
b) If, however, you declare that classical physics applies everywhere and that relativity and quantum mechanics must be wrong, then that is not right.
c) If you know that your soccer field is flat and work to that you are correct. Although, in fact, the Earth locally is highly variable with flat regions, high mountains and deep valleys and everything in between.
d) If, however, you declare the Earth to be flat globally (which is the flat-Earth theory), then you'd be wrong.
I would suggest to write another article, reformulating this one in a quite straightforward way, against the
"Flat Earth Theory Is Wrong" Fallacy.
It works, indeed, nicely on the soccer field near my home, and gives accurate predictions for trajectories of the ball.
Classical theories are approximations, not limitsYes, they are. Did you not read the article?
Also, approximations are not inherently wrong
Classical theories are approximations, not limits.If you have an "approximation", this suggest that it is an approximation of something. The aim of physical theories is to describe observations. If they do, they are good theories. In certain limits, classical theories work fine and they are good theories in those limits. What is meant by a theory being recovered as a limit of a different theory is that predictions agree to leading order as some model parameter is taken to zero. This is standard nomenclature. When the parameter is not exactly zero, but relatively close, yes you can use the classical theory as an approximation of the full theory, but this is conceptually different.
Ergo, saying classical physics is wrong is wrong is wrong!This statement just makes it clear that you have missed the entire point of the discussion, which is that what laymen consider the word "wrong" to mean is fundamentally different.
Classical theories are approximations, not limits. Ergo, saying classical physics is wrong is wrong is wrong!
Classical theory. Wrong but by so very, very little in everyday situations it is not worth the extra trouble using the correct theory.
And can we say the current theories are correct? As far as we know they are but as far as they knew at the end of the 19th century the classical theories were. Let us hope not, as where would be the fun in that?Since when is the limit of an approximation is considered to be "wrong" when it is used in that limit? That's like saying there is no point in even doing linear algebra or many-body physics, because these are all approximations (even valid approximations). If that's the case, then every single thing we use now is wrong, because I can guarantee you that no one has every managed to completely solve any of the many-body equations that described the behavior of your semiconductors, the behavior of current in a conductor, etc… etc.
The problem here is that among the general public, the word "wrong" has a very strong and distinct connotation. When something is wrong, you don't use it, or you don't do it. It is very black-and-white. Yet, this is not what is meant here, and in that sense, classical physics is definitely not wrong. So in that context, claiming that classical physics is wrong, is in fact, wrong!
Zz.
Classical theory. Wrong but by so very, very little in everyday situations it is not worth the extra trouble using the correct theory.
And can we say the current theories are correct? As far as we know they are but as far as they knew at the end of the 19th century the classical theories were. Let us hope not, as where would be the fun in that?
Thank you for the Insight article.
I apologise to everyone if this is a dumb question, but would you say Newton's laws would further reduce to Kepler's laws under some limiting case?No. Kepler's law is an "application" of Newton's laws, the same way the kinematics of a mass sliding down an inclined plane is an application of Newton's laws.
Zz.
Thank you for the Insight article.
I apologise to everyone if this is a dumb question, but would you say Newton's laws would further reduce to Kepler's laws under some limiting case?
The distinction does not appear in either the math or experiment may not be sufficient to conclude that they are the same theory or same fundamental concepts or same assumptions.The scientific method cannot distinguish between two models which make the same experimental predictions, even if they have different assumptions. Scientifically they are identical. As a result usually they are considered to be different interpretations of the same theory, particularly in Quantum Mechanics where this occurs frequently. They are not considered different theories, despite the different assumptions.
The distinction does not appear in either the math or experiment may not be sufficient to conclude that they are the same theory or same fundamental concepts or same assumptions.This is a very puzzling statement.
The argument isn't about "fundamental concepts" of "same assumptions". They are not! The postulates of SR is distinctively different than the classical Galilean transformation. That isn't the issue!
But when you have derived, under a certain limit, of the same mathematical form, then that theory can be logically shown to be able to reproduce all the results of that came out of the mathematical form!
I'm a bit surprised that this is even an issue. This is done in mathematics all the time! We manipulate our differential equations, for example, so that they can be in one of the known forms that results in one of the special functions. As soon as the mathematical form matches a known form, the work is done is showing what the solutions and the behavior of the solutions should be, because it has already been solved!
Zz.
By working the math. A lot of things that we may verbally or philosophically consider different are mathematically equivalent. You may think that you are drawing an important distinction between Newtonian and Relativistic mechanics, but in the v<<c limit this distinction is only in your mind and does not appear in either the math or experiment.The distinction does not appear in either the math or experiment may not be sufficient to conclude that they are the same theory or same fundamental concepts or same assumptions.
I agree with the author. However, he wrote, "…if there are more general and more accurate theories beyond QM, SR/GR, …".
Physicists say that SR expressions have been verified with accelerators. So, if there is any theory that gives a different expression, then it will not get along with results from the accelerators. This means that there is no way for a more accurate theory exists.These theories give you answers to questions SR cannot answer.
SR cannot tell you what happens with gravity. GR can. In the absence of gravity, GR is identical to SR.
SR cannot tell you what happens if fields are quantized. QFT (quantum field theory) can. If the quantization is irrelevant, QFT is identical to SR.
Physicists say that SR expressions have been verified with accelerators. So, if there is any theory that gives a different expression, then it will not get along with results from the accelerators. This means that there is no way for a more accurate theory exists.A more accurate theory must reduce to the SR expressions under the conditions covered by the accelerator experiments. It may diverge from SR in other conditions.
I agree with the author. However, he wrote, "…if there are more general and more accurate theories beyond QM, SR/GR, …".
Physicists say that SR expressions have been verified with accelerators. So, if there is any theory that gives a different expression, then it will not get along with results from the accelerators. This means that there is no way for a more accurate theory exists.I think you missed the point, and you also seem to be unaware of the history of physics.
We ALWAYS come up with more comprehensive and more accurate theories. That has always been the pattern, and there's nothing to say that this will stop. The issue of unifying general relativity within the QM/QFT picture is one such problem we have right now. So if there is a more encompassing theory, then this new theory will have to have, at some limit, the SAME form as SR/GR, because of the successes of SR/GR already. It is why I showed the mathematical derivation and showed how the mathematical form matches classical description in some limit.
Please look again at the original post and the MAIN POINT of that post, because it appears that you didn't get that story.
Zz.
I agree with the author. However, he wrote, "…if there are more general and more accurate theories beyond QM, SR/GR, …".
Physicists say that SR expressions have been verified with accelerators. So, if there is any theory that gives a different expression, then it will not get along with results from the accelerators. This means that there is no way for a more accurate theory exists.
What difference does it make if you get the old theory from an upper limit or any other arbitrary direction? My point was that SR is considering space and time as completly different things comparing to old mechanics. This does not make any sense. If I say that the assumptions are: time is relative and space is Riemaniann and you say: time is absolute and space is euclidian, how can we be talking about the same theory?
No, you are wrong. What I said was that the assumptions are different! If you look at how we treat all the experiments and particles / waves in quantum world, we see that space, time, energy and whatever are all different from what we knew from classical mechanics, which means, we cannot start to say that there exists a derivation from one to another, as they were talking, ever, about the same thing. Again, if you start with different assumptions how can you end up with theories converging at a limit that has been chosen to find a connection between them?
I am not saying that Newtonian Mechanics is wrong. this has nothing to do with being right or wrong. I'm talking about how do we explain an theory evolution without wanting to find convergencies that were created just to make understanding easier.I agree with Orodruin with more knowledge, the parameters for the theory of Physics have changed. Now since Newtonian physics work and more detail is known, then retro fitting more defined parameters to the limited parameters makes sense to me. I would say doing this would ensure if the more defined parameters cannot be canceled out to fit within the limited parameters, then the new theory cannot really encompass the basics of physics. This theory then would mean it represents another reality. Which I know is all relative. However if elements on Earth can be found in space, then when chemistry is brought in the picture, physics in space have to relate to what happens on Earth. With that said, retrofitting quantum equations to fit Newtonian physics will ensure that with more parameters added that the idea has a sound basis to be built upon.
Now the theory of assumptions can be a matter of discussion, but I feel if quantum can explain mechanical in mathematical form then assumptions have to be reevaluated within the confines that mechanical theory works. So I love this article.
In my view, I say that any major scientific development is a generalization procedure (in a very loose sense).
I don't know much instances where a theory was completely denied from the core. This is obvious because science is based on observation and experiment that is reproducible. Even geocentrism is not "wrong". Purely in terms of orbits, it is simply a matter of where the origin is defined to (the Earth or the Sun). Of course, we know that heliocentrism was right in light of new experimental evidence, but it still encompasses what was developed in geocentrism. If we understand heliocentrism (how the stars and planets move), then we can also understand geocentrism (how the sky looks like from a planet).
Similarly, classical physics is a specialized case/formulation of quantum mechanics. They are not "wrong". Non-relativistic quantum mechanics is a specialized case of QFT. They are not "wrong" (although I understand that QFT is still essentially QM and not precisely a good analogy).
If there is any new theory in physics, then they are going to encompass what has already been developed but more generalized, and can be used to explain more than we used to. It won't "deny" anything.
Great article. I cannot agree more.
I prefer to consider theories as "useful" or "not useful" for given applications rather than "right" (true) or "wrong". A theory is useful if it makes predictions that are sufficiently accurate for my purpose.You will notice that I tend to use the word "valid", rather than right, true, etc… But at some point, this becomes a matter of semantics, i.e. what exactly does one mean when one say "right" or "wrong". One doesn't usually use something, or do something, that is wrong. For classical mechanics, we use it a lot!
But the fact is, there were many occasions in my undergraduate (and graduate) education where the wrongness of the prevailing theory (inability to accurately predict an experimental result) was used to justify development of a new theory, and often classical physice was the prevailing theory portrayed as wrong in the circumstances described.But are they "wrong" or simply not applicable or not accurate enough after a certain point? Your electronics use Ohm's Law, but I can show you a lot of circumstances where it doesn't work because the assumptions that Ohm's Law were derived from are no longer applicable. So is it wrong, or is it simply that it isn't meant to be used in that situation?
The discussion leading to eqns 6 and 7 (and eqns 6 and 7 themselves) breaks down in the case of chaotic classical motion, and it is still something of a mystery how QM gives rise to chaotic classical motion in the limiting case.The article is not claiming that it has solved the classical-quantum boundaries. Far from it. Mesoscopic scale physics is still a very active area of research, and the classical-quantum "transition" (I'm using the pedestrian definition of this word) is still unknown. And I can go all day talking about emergent phenomena that can't be simply derived from all the basic interactions (superconductivity). However, there are still indication that one can get back the classical picture under certain circumstances. This is a piece of information that is not known by many members here who often made the claim that classical physics is wrong. Any physics student is aware of the derivation that I did in the article. It isn't news. It IS news to many who are not aware of such connection when they think that we shouldn't use classical physics anymore when it has been superseded by QM/SR/GR.
THAT is the main purpose of the article.
Zz.
I prefer to consider theories as "useful" or "not useful" for given applications rather than "right" (true) or "wrong". A theory is useful if it makes predictions that are sufficiently accurate for my purpose.
But the fact is, there were many occasions in my undergraduate (and graduate) education where the wrongness of the prevailing theory (inability to accurately predict an experimental result) was used to justify development of a new theory, and often classical physice was the prevailing theory portrayed as wrong in the circumstances described.
2. Classical physics has been shown to be derivable from SR and QM under special conditions that apply to our ordinary situation.
3. Any theory MUST have the ability to show that it merges to the classical description when applied to ordinary situation.
4. This can only be shown mathematically. It cannot be shown convincingly via hand-waving or qualitative arguments. It is the equivalent mathematical form that shows that one theory can derive the other.
The discussion leading to eqns 6 and 7 (and eqns 6 and 7 themselves) breaks down in the case of chaotic classical motion, and it is still something of a mystery how QM gives rise to chaotic classical motion in the limiting case. Some specific cases from atomic physics have received a lot of attention:
V = -1/r + B^2(x^2 + y^2)/8 (Model for hydrogen atom in a magnetic field)
V = -1/r + (Z – 1) exp(-ar) + Fz (Model for an alkali atom in an electric field)
I've published several papers studying the above two Hamiltonians, and I assure you there is no mathematical description showing how the classical solution of the Hamiltonian arises from the quantum solution in cases where the parameters give rise to strongly chaotic motion in the classical solution. Numerous other authors have reached the same conclusion in studying these problems.
I look at the epistemological question in physics analogous to the germ theory of disease in biology. Just as history gave rise to more and more diseases where the germ theory was not applicable, history gave rise to more and more cases where classical physics was not applicable. It is really a matter of definition whether one says "the germ theory of disease is wrong" or "here are the list of known cases where the germ theory of disease is known not to apply." Given that at one time, classical physics was throught to be universal, the position that it is wrong is defensible. But at some point the debate is silly, and it is more reasonable to address theories based on their usefulness rather than on their truth.
Euclidean geometry is similar. Before Einstein, it was widely held to be an exact and universal description of the physical world. Now we know that is not true. But it sure is useful and an exceedingly accurate approximation for most purposes.
Interestingly enough, with QM and the idea of quantized lattice vibrations (phonons), the old concept of "corpuscular heat" of Caloric Theory is not totally crazy when applied to thermodynamics in solids.I love this! There was imagination to "Caloric".
Even so – I am cautious about taking this too far. The mental magic that allowed many to countenance a "negative weight" concept in the cause of "phlogiston" is one model where it's subsequent usefulness in practical calculation and prediction, is pretty much trashed by the manifest evidence of a new element, and a much more useful concept!
When I say "Classical Physics is not wrong", I do not mean any and every disproved notion. Within the accuracy by which we can usually verify our experiences, I mean the whole of classical physics "laws" that have never seen a single exception. It has to be an exception glaring and obvious, so that humans can recognize that it might belong in the same bin as phlogiston.
To know that something else might be going on, one needs to go to exceptional precision, and even then get used to the idea that there is a built-in uncertainty that messes with how well one can determine other values involved.
But as I've said earlier, it is no longer that common that an older theory is discarded wholesale. This is because many of our older ideas are actually valid within the realm that they are applicable.
It was certainly more common with ideas from the 19th Century, where our methods of detection and awareness of our world are significantly less developed. The old idea of Caloric Theory is one clear example, where one of the first attempts at formalizing our understanding of thermodynamics has been basically discarded.
Interestingly enough, with QM and the idea of quantized lattice vibrations (phonons), the old concept of "corpuscular heat" of Caloric Theory is not totally crazy when applied to thermodynamics in solids.
Zz.
Reading these posts makes me wonder how "wrong" some "outdated" approximation has to be, to cease to be useful.
I mean this not only in the day-to-day practical sense, but also in contributing to the wonderful human sense of pattern recognition and making those insight connections to come up with a whole new theory or concept that incrementally relegates the "old" into being an approximation. The new is built on the scaffold of the old – even if one ends up junking the entire scaffold!
Putting aside the Newtonian vs Einsteinian comparison, consider something older by Tycho Brahe. Apparently impressed by the mathematical benefits of a Copernican heliocentric system, but unable to imagine a "huge heavy sluggish Earth" moving at speed, he came up with a geoheliocentric model that was accurate. Tycho was obsessed with accuracy, and gathered the best measurements of the time.
Yes yes – we get it that Kepler, Newton, and others had a later different, and simpler, insight, and that they got there much on the back of Tycho's data, but Tycho could predict with the best of them! He could say when an eclipse would happen, or say when and where a planet would be would be when occulting a star. In his own mind, and among those who depended on his data, Tycho had a right to believe his model was the way celestial bodies really moved!
Take away Tycho, and his "wrong" model, and you take away one of the "shoulders" Newton and others would stand upon to see further.
Even now, however well we think we know where celestial bodies are, and how they move, they had better not be too far from where Tycho thought they should be! We now have a wonderful Quantum Mechanical description of the way things are, an absurdly abstract non-intuitive fairy story of the charmed and strange and sticky that agrees with experiment to enough decimal places to be impressively compelling.
Perhaps in the fine tradition of Maxwell (adding an unmeasured "displacement current" to make the equations come out right), because it seemed the right thing to do, the way things are need to be described with some sort of model that agrees with experiments. It is when we postulate mathematical fictions (however useful), we need to keep a watch on whether they are more than a calculation aid!
No-one responded to this comment on Facebook (https://www.facebook.com/groups/2204629320/permalink/10156235771439321/?comment_id=10156240941494321), so I'll make it here also and make a few additional comments to reflect the discussion above, "Not only is classical physics not wrong, it is more capable than generally understood. If we present classical mechanics as a commutative algebra of operators together with a noncommutative algebra of transformations constructed using the Poisson bracket, all acting on a Hilbert space in a Koopman-von Neumann formalism, a random field CM can even be equivalent to a QFT if there is a natural complex structure (which there is in the case of electromagnetism, provided by the Hodge dual)."
This obviously leads in a slightly different direction than either ZapperZ's article or the comments above. Seeing one concern expressed in the comments above, I'll also note that I take not only the Lagrangian and Hamiltonian formalisms to be part of "Newtonian physics", but also Liouvillean probability densities over phase space and the Koopman-von Neumann formalism, and the extensions into issues of analysis (random fields, say, citing my own preference because they they can be made to parallel quantum fields so closely, but there are other stochastic approaches) that are required to discuss probability densities in field theory cases.
A further comment, about special relativity: the wave equation, the Klein-Gordon equation, and any differential equation that is Lorentz invariant, fit into the Lagrangian, Hamiltonian, Liouvillean, and Koopman-von Neumann formalisms well enough, so there's not any necessity to consider a limit as the speed of light is much larger than characteristic velocities. Just solve the equations.
I should be open about this comment being part of an effort to get more good mathematical physicists to look at and send me comments on https://arxiv.org/abs/1709.06711. The math there has been stable for many months, but the abstract and introduction do not discuss the relationship between random fields and quantum fields as clearly as I would like (nor as clearly as those people who have looked at the paper would like). I am now very close to submitting to a journal, so if you decide to have a look please be quick! I will be happy to send a copy of the paper as I currently have it to anyone who expresses interest.
You can make prediction of the consequences of a particular spacetime geometry and then measure those consequencesNo, you can make a prediction of the consequences of particular solutions of particular equations, and then compare the predictions with measurement. But the equations don't have labels on them that say "these equations describe a spacetime geometry". Spacetime geometry, as I said in a previous post, is an interpretation of the equations. You don't need an interpretation to make predictions and compare them with measurements. Interpretation is a conceptual crutch for us humans, because we don't naturally think in equations, so we need some kind of story to tell about what the equations "mean". But the "spacetime geometry" story is not the only story you can tell about the equations of GR.
When someone says 'You cannot "measure" spacetime. You can make prediction of the consequences of a particular spacetime geometry and then measure those consequences.', isn't that way for every observable in physics? what are we measuring when we talk about forces? forces themselves? what about eletrons? what are particles anyway? is it a useful concept (dimensions neglected) or something else? and mass, energy?
You see, we started to discuss some fundamental stuff in my opinion and, for whatever reason Zz wrote his article, it is very important to define, or at least try to, concepts that will be used throught the text. does anyone know if Einstein was particularly worried about not being able to replicate newtonian mechanics during his GR times? I am really curious about this.
The problem was: "Some guys here are saying that Newtonian Mechanics is wrong because GR and QFT are more fundamental than it, so, in order to prove them wrong let's derive newton's laws from GR (or SR) or QM.". I guess they will continue to think it is wrong. If we say, using some historical background and then, progressively showing that Newtonian Mechanics is really precise within macroscopic phenomena (ordinary daily events), there you go, you don't need to sustain that we could find a convergence from either GR or QM to it, and from that point on use this convergence argument as the truth. We would not need to perform an anachronistic analysis.
someone said that we can recovery NM from QM, using some kind of limit on ℏ→0, where can I find more info about this?
Anyway, sometimes we can't really explain our view on complex issues, but I am happy to read so many interesting replies.
PS: in my first reply I was talking about anecdotal examples, I didn't mean physics is outside the experimental examples.
Ah, ok. Yes, from a philosophical point of view, I agree the question is undecidable. The spacetime curvature interpretation of GR is, strictly speaking, an interpretation, not a claim about "how things really are". It just happens to be a very, very useful interpretation, so much so that physicists routinely talk about it as if it were a fact.For what it's worth I am with Feynman who thinks the geometrical interpretation is marvelous – it's hard to think its not actually true – but strictly speaking like the difference between SR and LET you cant really prove it. I have read his lectures on gravitation and he starts with flat space-time and spin 2 particles. You still get the EFE's but if space-time actually curved is not so clear.
Later I discovered Lovelock's Theorem that put it more in context for me. Thinking of the metric as a field or it's natural geometrical interpretation doesn't make any difference – the theorem says you get the same result – but strangely only in 4 dimensions which is rather interesting.
Thabks
Bill
It just happens to be a very, very useful interpretation, so much so that physicists routinely talk about it as if it were a fact.That is indeed a problem. In the Newtonian limit of GR, for example, the Christoffel symbols naturally become the force of gravity. So although we speak of gravity in GR as not being a force, in fact there is mathematical quantity in the theory that does serve that role. Choosing to not interpret that way is a matter of philosophy and can be discarded as needed. But that common interpretation probably serves to exacerbate the “Newtonian physics is wrong” impression.
He posted quite a bit until it became invested with too many cranks, but mentioned a few times it was a an essentially undecidable philosophical question whether space-time was curved or was flat and simply acted like it was curved.Ah, ok. Yes, from a philosophical point of view, I agree the question is undecidable. The spacetime curvature interpretation of GR is, strictly speaking, an interpretation, not a claim about "how things really are". It just happens to be a very, very useful interpretation, so much so that physicists routinely talk about it as if it were a fact.
Can you give a particular reference? I've read a fair number of Carlip's papers and I'm not sure I've seen him expound the "unobservable flat background" view.It was from when I posted a lot on sci.physics.relativity. He posted quite a bit until it became invested with too many cranks, but mentioned a few times it was a an essentially undecidable philosophical question whether space-time was curved or was flat and simply acted like it was curved.
I must say that was at least 10 years ago so may have changed his mind. I do know he isa very approachable guy and I don't think he would mind anyone asking him what his current view is. Mine is he is correct – and until he mentioned it, it never even occurred to me – it was sort of a revelation..
Thanks
Bill
That is Steve Carlip's viewCan you give a particular reference? I've read a fair number of Carlip's papers and I'm not sure I've seen him expound the "unobservable flat background" view.
My understanding is that at least one possibility for a quantum gravity is a quantum theory similar to all the others, in which gravity is a force in a similar sense to electromagnetism (we can't make it work properly, but the same is true of every other post-GR theory we've tried so far). All the spacetime curvature stuff is explicable and understandable in those terms, basically because there's nothing that doesn't interact with the graviton fieldYes, this is correct. And it's another good illustration of why the term "wrong" isn't useful when talking about different theories of physics. See further comments below.
why does everyone get so emotional if anyone says the obvious about Classical Mechanics?Because what you are saying is "obvious" is not anything of the sort. If Classical Mechanics is "wrong", how come it works so well?
Instead of using the word "wrong", it's much better to focus on what predictions the different theories make, and in what regimes they are accurate, or more precisely accurate enough for practical use. By that criterion, Classical Mechanics makes accurate enough predictions in a very wide regime–it's good enough to design bridges and buildings that don't fall down, design spacecraft that can arrive at a distant planet within a second of the predicted time after years of travel, predict how close asteroids will come to the earth several decades in advance, etc. A theory that works that well is not usefully described by the word "wrong".
Moreover, using words like "wrong" implies that there is a "right" answer–that, for example, whatever GR says about "reality" is "right". But we don't know that. We only know that GR, as compared to Classical Mechanics, makes accurate predictions over a wider regime–and that Classical Mechanics can be derived as an approximation to GR under appropriate conditions.
if you were to say that GR is wrong (on this point) and gravity is a force, people would be likely to react by saying "that is an interesting theory, tell me more…"Yes, and that's the problem. People shouldn't be thinking "interesting idea" just because you say GR is "wrong". They should be thinking "interesting idea" if you say "I have a theory that makes accurate predictions over a wider regime than GR, and that can derive GR as an approximation under appropriate conditions". But that sounds a lot less exciting than "wrong", so people use the more exciting word instead of the word that best conveys the actual situation. IMO that's a bug, not a feature.
But the curvature isn't "real" in some philosophical sense – there is an unobservable flat background.This is bit off topic but I think it interesting enough to mention. That is Steve Carlip's view (look him up if you don't know him). I have been reacquainting myself with GR recently since I find as a mentor I answer more of these queries. Anyway if you don't know Lovelock's theorem you might find it sheds light on this.
Thanks
Bill
@Ibix for example in #56 accepted the premise of the question.English was not my best subject – but that was not my reading. I still do not know what worries you.
We basically discuss physics here – not semantics. I have given you the answer – I think others have basically said the same thing except expressed somewhat differently and did not bring up some of the technicalities I did.
As I mentor I do not like seeing threads going south – cant you just take on board what I said and not worry about your perceptions of other stuff. I mentioned about symmetry – this is a very profound discovery of modern physics – it's much more important and interesting than worrying about the tone of replies or what you perceive about the attitude of some people in threads. I can assure you people will soon tire of it – its counter productive. We can go down the symmetry path as the unifying concept of QM and Classical Mechanics. When I found out about it, it literally changed my life. A staff emeritus here teaches this stuff – he waits in silence while it sinks in because his students are – well – as I was – in shock at its implications.
Just give the word and I will take you on this journey.
Thanks
Bill
Just who are you talking about here? I don't do that.Glad to hear it.
It is something I have noticed – I'm surprised if you haven't also noticed.
@Ibix for example in #56 accepted the premise of the question.
Why is so much energy invested in jumping on people who happen to say Classical Mechanics is "wrong"?Just who are you talking about here? I don't do that. I explained what classical mechanics was in post 44 – its simply QM in a certain regime. I explained why it was quite unlikely QM was wrong in regimes we currently can probe. Exactly what is your beef – you seem to be arguing for arguments sake.
Regarding GR it isn't quite what you say – forces exist in GR. However it a bit subtle and you should really start a new thread if that's what you want to discuss.
Thanks
Bill
This is like someone dives in and rescue a drowning victim, and you're criticizing the color of the shoes that the rescuer is wearing.
I think I'm done entertaining this triviality here.
Zz.Please don't take it personally.
I have already said that I think your first three points under the Moral of the Story are very well put.
The excessive (IMHO) intolerance of people using "Classic Mechanics" and "wrong" in the same sentence is something I have noticed a lot, and your article, and the discussions in the thread which follow it, are just the particular occasion for discussion of it. I wasn't intending to ctrticise you personally.
That is a very fair point. But if you were to say that GR is wrong (on this point) and gravity is force, people would be likely to react by saying "that is an interesting theory, tell me more…" People are unlikely to write polemical articles which say things like "There is a need to debunk that idea, and it needs to be done in the clearest possible manner…"
My query is about the difference in tone – why does everyone get so emotional if anyone says the obvious about Classical Mechanics?This is like someone dives in and rescue a drowning victim, and you're criticizing the color of the shoes that the rescuer is wearing.
I think I'm done entertaining this triviality here.
Zz.
But do we? My understanding is that at least one possibility for a quantum gravity is a quantum theory similar to all the others, in which gravity is a force in a similar sense to electromagnetism.That is a very fair point. But if you were to say that GR is wrong (on this point) and gravity is force, people would be likely to react by saying "that is an interesting theory, tell me more…" People are unlikely to write polemical articles which say things like "There is a need to debunk that idea, and it needs to be done in the clearest possible manner…"
My query is about the difference in tone – why does everyone get so emotional if anyone says the obvious about Classical Mechanics?
I wonder whether maybe it is being a bit oversensitive to lambast people who say that Classical Physics is "wrong".
Put yourself in the shoes of a student. They study Classical Mechanics and are told that gravity is a force. They then study GR and are told that gravity is not a force. It is only natural, and an ordinary use of language, for them to say they have found out that Classical Mechanics is wrong.
Of course we may say that it is not all wrong and/or it is a good and useful approximation in many everyday circumstances, but it is technically correct to say that, taken as a whole, it is wrong. Or, at the very least, it is a forgivable use of language to say that, taken as a whole, it is wrong.
If the correct answer to a calculation, according to SR is 14.9999999999 and Classical Mechanics gives an answer of 15, it is correct to say that 15 is wrong. It may be only slightly wrong and it may be quite sufficient for the practical purposes we have in mind and have been much easier to calculate, but, nevertheless, technically it is wrong.
Why is so much energy invested in jumping on people who happen to say Classical Mechanics is "wrong"?Then everything is technically wrong, because you verify ANYTHING up to the resolution and precision of the experimental instrument and methods. After all, we don't know if QM, SR, and GR are the final words in our understanding of our universe.
No one is "jumping" over anyone here. The issue is that many, if not most, of the members who previously brought up this issue were not aware of the ability of QM/SR/GR to derive the classical/Newtonian description! This is a FREE lesson that many of us who went through undergraduate physics have seen, and which they haven't. So this is why I find it a bit odd that you are criticizing something like this in the effort to educate and inform those who were never aware of such things.
But I guess there is just no pleasing some people on the sidelines…..
Zz.
If we believe GR is correct to say gravity is not a forceBut do we? My understanding is that at least one possibility for a quantum gravity is a quantum theory similar to all the others, in which gravity is a force in a similar sense to electromagnetism (we can't make it work properly, but the same is true of every other post-GR theory we've tried so far). All the spacetime curvature stuff is explicable and understandable in those terms, basically because there's nothing that doesn't interact with the graviton field (@PeterDonis will correct me if I'm wrong, I'm sure). But the curvature isn't "real" in some philosophical sense – there is an unobservable flat background.
if GR is our theory, why is is wrong to articulate the logical consequence that Classical Mechanics is wrong to say that gravity is a force?Because we don't know that GR's concepts are right, only that its predictions are better.
Because every point you made in this post also applies to relativity and quantum compared to whatever the successor theory we eventually develop is. And we would have to suspect the same of that successor theory, because there will always be regimes where we won't have tested it. So if classical mechanics is wrong in these terms, so is every theory. That doesn't seem like a helpful use of the term "wrong".I take the point that we keep making new discoveries and from time to time revise our theories so it is a fair bet that our current theory – GR say – will be revised in future. But given that our current theory is GR and GR says that Classical Mechanics is wrong about gravity being a force (or example) I can't see why we have to pussyfoot around in saying that we believe Classical Mechanics is wrong on this point at least. If we believe GR is correct to say gravity is not a force then it logically follows that we believe Classical Mechanics is wrong to say that gravity is a force.
Of course we all might be completely wrong at the end of the day when we discover theory X, but for the moment, if GR is our theory, why is is wrong to articulate the logical consequence that Classical Mechanics is wrong to say that gravity is a force?
Why is so much energy invested in jumping on people who happen to say Classical Mechanics is "wrong"?Because every point you made in this post also applies to relativity and quantum compared to whatever the successor theory we eventually develop is. And we would have to suspect the same of that successor theory, because there will always be regimes where we won't have tested it. So if classical mechanics is wrong in these terms, so is every theory (or at least, we must always suspect so). That doesn't seem like a helpful use of the term "wrong".
I wonder whether maybe it is being a bit oversensitive to lambast people who say that Classical Physics is "wrong".
Put yourself in the shoes of a student. They study Classical Mechanics and are told that gravity is a force. They then study GR and are told that gravity is not a force. It is only natural, and an ordinary use of language, for them to say they have found out that Classical Mechanics is wrong.
Of course we may say that it is not all wrong and/or it is a good and useful approximation in many everyday circumstances, but it is technically correct to say that, taken as a whole, it is wrong. Or, at the very least, it is a forgivable use of language to say that, taken as a whole, it is wrong.
If the correct answer to a calculation, according to SR is 14.9999999999 and Classical Mechanics gives an answer of 15, it is correct to say that 15 is wrong. It may be only slightly wrong and it may be quite sufficient for the practical purposes we have in mind and have been much easier to calculate, but, nevertheless, technically it is wrong.
Why is so much energy invested in jumping on people who happen to say Classical Mechanics is "wrong"?
"not incompatible" means "compatible"?
If that is so, then I do NOT see those two as being compatible. To say that Newton's laws are wrong, and then to turn around and use it, is an inconsistent act.
To say that it is accurate over a certain limit, and then to turn around and use it within those limits, is NOT an inconsistent act.
Unfortunately, this is now semantics. But this is not how people who have asked this on this forum think, because they are under the impression that we should NOT be using Newton's laws, under ANY limits, because it has been shown to be "wrong" by QM and SR/GR. THAT is the argument that I'm countering against.
Zz.You have – no doubt accidentally – skipped over the words in brackets in "1. Newton was wrong (about a lot of things)"
To say that Newton's laws are wrong, and then to turn around and use it, is an inconsistent act.
To say that it is accurate over a certain limit, and then to turn around and use it within those limits, is NOT an inconsistent act.Particularly well said.
But there are also cases where practically identical issues crop up repeatedly where my first instinct has been shown to be accurate. If I get $1 for every time I read …..
This is not simply an issue on this forum. It is everywhere. It is why someone like Dan Siegel at Stony Brook got so fed up with the same, repeated stuff that he got that he made his Are You A Quack page, because no matter how much you think things are different, I can easily argue how much many things are alike.
Zz.Well I haven't done a scientific study, and maybe things were different in the past, but from a limited search there did seem to be quite a lot of posters who received polemical replies to their posts when seemed to be based on assumptions about them not actually justified by what they were saying. And their bewildered reaction seemed to indicate that the polemic was not on target.
That is quite understandable in a way, but if I can give a personal perspective: I have been visiting and posting on this forum only for a couple of months and one of the things that immediately struck me was that that some posters – often several at a time – seemed to react to things I posted in ways which didn't seem to be justified by what I was actually saying. I then did a bit of searching and discovered that this happened a lot to posters who said anything which came near certain subjects. If you get a lot of posters of a certain ilk it is easy to get into a mindset where you assume people have a certain perspective and react to that presumed perspective rather than to what they are actually saying. But for the person on the receiving end this can be quite confusing… until they work out what is happening when it becomes merely annoying!But there are also cases where practically identical issues crop up repeatedly where my first instinct has been shown to be accurate. If I get $1 for every time I read …..
This is not simply an issue on this forum. It is everywhere. It is why someone like Dan Siegel at Stony Brook got so fed up with the same, repeated stuff that he got that he made his Are You A Quack page, because no matter how much you think things are different, I can easily argue how much many things are alike.
Zz.
And like I said, that is now a matter of semantics and personal preference. I stated that based on many years of observations of members here in this forum when we repeatedly dealt with such topics.
Zz.That is quite understandable in a way, but if I can give a personal perspective: I have been visiting and posting on this forum only for a couple of months and one of the things that immediately struck me was that that some posters – often several at a time – seemed to react to things I posted in ways which didn't seem to be justified by what I was actually saying. I then did a bit of searching and discovered that this happened a lot to posters who said anything which came near certain subjects. If you get a lot of posters of a certain ilk it is easy to get into a mindset where you assume people have a certain perspective and react to that presumed perspective rather than to what they are actually saying. But for the person on the receiving end this can be quite confusing… until they work out what is happening when it becomes merely annoying!
Of course not, the Newtonian limit is part of relativity and QM, not part of Newtonian mechanics. I have read the context and your statements repeatedly show this misunderstanding.Anyway. I am glad we are now agreed!