The Quantum Mystery of Wigner’s Friend

In this Insight I will introduce the quantum mystery called “Wigner’s friend” using Healey’s version [1] of Frauchiger and Renner’s (FR’s) version [2] of Wigner’s version [3]. As with much of physics, the explication becomes more succinct and comprehensible with each successive rendering. I will show how this mystery results from treating classical information (behaving per Boolean algebra) as quantum (behaving per non-Boolean algebra), contrary to spatiotemporal-constraint-based explanation in the “blockworld (block universe) view” aka “all-at-once view” (Wharton) aka “God’s-eye view” (Wilczek). Essentially, when FR ask whether or not quantum mechanics can be applied to itself and answer negatively, they have really attempted to apply quantum mechanics to a classical system, not a quantum system. My presentation differs substantially from that of Healey, so you should read the original papers if you’re interested in their rendering of the mystery. I should say this is in no way an improvement on Healey’s version.

The whole point of the Wigner’s friend scenario is that someone (Wigner in the original story) makes a quantum measurement of someone else (Wigner’s friend) who made a measurement of some quantum system. For that to be possible, Wigner’s friend must be isolated (screened off) from Wigner and the rest of the universe. Being screened off means Wigner’s friend cannot share any classical information with the universe. This introduces obvious technical and conceptual difficulties.

Technically, one would have to keep Wigner’s friend and his entire lab from interacting with the universe, e.g., no exchange of photons. That’s certainly beyond anything we can do now, but more importantly, this means the classical information possessed by the friend with lab while screened off is not accessible to Wigner or anyone else in the block universe. [Note: The classical information could just as well be contained in a computer with no human agent involved.] Since the block universe is precisely all shared, self-consistent classical information, the friend’s classical information while screened off, being unshared/inaccessible to everyone else, is not even part of the block universe and therefore not a part of objective reality. And that means, among other things, that there is no way to establish relative coordinate directions between Wigner’s frame and his friend’s frame. The alignment of Cartesian frames and synchronization of clocks between observers in the block universe is already a problem that must be overcome to transfer information via quantum systems [4]. That is because we must first be able to relate Hilbert space vectors involving, say, polarizer orientations between the two isolated frames in order to use the formalism of quantum mechanics (QM). Thus, after being measured by Wigner, it is impossible for the friend’s classical results to contradict the shared classical information of the block universe, as required to refute objective reality.

Conceptually, if Wigner’s friend is measuring $\hat{x}$ with the eigenbasis $|heads\rangle$ and $|tails\rangle$ (a “quantum coin flip”), it must be possible for Wigner to measure $\hat{w}$ with the eigenbasis $|heads\rangle – |tails\rangle$ and $|heads\rangle + |tails\rangle$, even though we can’t imagine what that means in terms of a coin flip. This is another crucial point that is ignored in analyses of Wigner’s friend.  In quantum mechanics, every Hilbert space basis unitarily transformed from the eigenbasis of some measurement operator is the eigenbasis of some other measurement operator and therefore constitutes something we can measure, e.g., Stern-Gerlach magnets or polarizers rotated in space giving rise to rotated eigenbases in Hilbert space. Proietti et al. did an experiment [5] they claimed was Wigner’s friend and while that claim is false (see Silberstein & Stuckey [6]), they did give an interesting hint as to what this rotated Hilbert space basis represents (again, see Silberstein & Stuckey [6]). Anyway, as I will show, the tacit introduction of these inconsistencies is what leads to the inconsistencies (inconsistent, shared classical information in the form of shared measurement outcomes) associated with the Wigner’s friend experiment. And, as Baumann & Wolf (BW) show [7] and I will introduce, there are other approaches to QM which do not suffer such inconsistencies.

Thus, the bottom-line question for the Wigner’s friend experiment is whether or not a person (such as Wigner’s friend) making a quantum measurement can themselves be treated consistently as a quantum system by someone else (such as Wigner). As we will see, the answer is “yes,” as long as the friend does not share classical information with the universe while screened off, i.e., while being treated as a quantum system. So, there is no size limit to the applicability of quantum mechanics as some have asserted based on FR. The problem is, the way Wigner’s friend is typically cast, the friend employs a measurement-update rule (sometimes associated with “wave function collapse”) while Wigner assumes the friend and his lab (to include their measurement records and memories) continue to evolve unitarily per the Schr$\ddot{\text{o}}$dinger equation. BW call this “subjective collapse” and show that even in the simplest version of Wigner’s friend, the sharing of inconsistent classical information can result. I will provide a similar example below. According to our constraint-based explanation, since this possibility allows for self-inconsistent shared classical information, the answer to this bottom-line question is “no” under these circumstances. The whole point of the constraint in the block universe (such as Einstein’s equations) is to ensure that the shared classical information composing the block universe is self-consistent. I begin with a presentation of Wigner’s friend per Healey showing how subjective collapse leads to the sharing of inconsistent classical information. Then I will show how proper treatments per the “standard” or “relative-state” formalisms for QM contain no such inconsistency.

There are four agents in this story — Xena who makes a quantum measurement $\hat{x}$ on quantum state c in her lab X and then sends a quantum state s to Yvonne, Yvonne who makes a quantum measurement $\hat{y}$ on s in her lab Y, Zeus who makes a quantum measurement $\hat{z}$ or $\hat{x}$ on X pertaining to Xena’s $\hat{x}$ measurement, and Wigner who makes a quantum measurement $\hat{w}$ or $\hat{y}$ on Y pertaining to Yvonne’s $\hat{y}$ measurement. So, we have two “Wigners,” i.e., Zeus and Wigner, and two “Wigner’s friends,” i.e., Xena  (Zeus’s friend) and Yvonne (Wigner’s friend). The first assumption of FR is that it is possible for Xena and Yvonne to behave as quantum systems for Zeus and Wigner to measure, i.e., there are no size restrictions on what can behave quantum mechanically. Again, I agree that it is possible to screen off Xena and Yvonne with the caveat that those systems being treated quantum mechanically per non-Boolean algebra are not exchanging classical information with the universe per Boolean algebra. I now explore the implications of violating that caveat via subjective collapse as in FR. The starting state c for Xena is

\begin{equation} \frac{1}{\sqrt{3}}| heads \rangle + \frac{\sqrt{2}}{\sqrt{3}}| tails \rangle \label{c}\end{equation}

The eigenbasis for Xena’s $\hat{x}$ measurement is simply $| heads \rangle$ and $| tails \rangle$ with eigenvalues heads and tails, respectively. If the outcome of her measurement is heads, she sends state s

\begin{equation} | – \rangle  \label{s+}\end{equation}

to Yvonne. If the outcome of her measurement is tails, she sends state s

\begin{equation} \frac{1}{\sqrt{2}}\left(| + \rangle + | – \rangle \right) \label{s-}\end{equation}

to Yvonne. Again, if $| + \rangle$ and $| – \rangle$  refer to orientations in space, e.g., polarizers or Stern-Gerlach magnets, their meaning between Xena and Yvonne is problematic, since their labs are isolated from one another. The sharing of such classical information is crucial for the modeling of the block universe per the very meaning of the Hilbert space structure, so ignoring this point is to introduce an inconsistency. But, as with the original papers, we will proceed to find its implications.

The second assumption of FR is that there is only one outcome for a quantum measurement, so Xena does not measure both heads and tails and send both versions of state s. Now, assuming subjective collapse, Xena and Yvonne’s labs are behaving quantum mechanically (evolving unitarily) according to Zeus and Wigner, so Xena and Yvonne’s labs are entangled in the state

\begin{equation} |\Psi \rangle = \frac{1}{\sqrt{3}}| heads \rangle | – \rangle + \frac{\sqrt{2}}{\sqrt{3}}| tails \rangle \left( \frac{1}{\sqrt{2}}\left(| + \rangle + | – \rangle \right)\right) = \frac{1}{\sqrt{3}}\left(| heads \rangle | – \rangle + | tails \rangle | + \rangle + |tails \rangle | – \rangle \right)\label{Eq13}\end{equation}

per Eqs. (\ref{c}), (\ref{s+}) and (\ref{s-}) for Zeus and Wigner (this is Eq. (13) in Healey’s paper). Assuming Xena and Yvonne’s labs evolve unitarily means Zeus and Wigner can make measurements of Xena and Yvonne’s labs in any rotated Hilbert space basis they choose. In addition to the measurement $\hat{x}$ with eigenbasis $|heads\rangle$ and $|tails\rangle$, Zeus has the option of measuring $\hat{z}$ with eigenbasis

\begin{equation}
\begin{split}
|OK \rangle_Z = &\frac{1}{\sqrt{2}} \left(|heads \rangle – |tails \rangle \right)\\
|fail \rangle_Z = &\frac{1}{\sqrt{2}} \left(|heads \rangle + |tails \rangle \right)\\\label{zeus}
\end{split}
\end{equation}

And, in addition to the measurement $\hat{y}$ with eigenbasis $|+\rangle$ and $|-\rangle$,  Wigner has the option of measuring $\hat{w}$ with eigenbasis

\begin{equation}
\begin{split}
|OK \rangle_W = &\frac{1}{\sqrt{2}} \left(|+ \rangle – |- \rangle \right)\\
|fail \rangle_W = &\frac{1}{\sqrt{2}} \left(|+ \rangle + |- \rangle \right)\\\label{Wigner}
\end{split}
\end{equation}

Again, this introduces another inconsistency with the block universe of shared, self-consistent classical information, i.e., the classical information must be intelligible. First, we have already pointed out how the relative orientations of Stern-Gerlach magnets or polarizers are needed to make sense of Wigner’s measurements of Yvonne’s lab and that this constitutes shared classical information forbidden by the assumption that Yvonne’s lab is screened off from Wigner. Second, we also have a problem of intelligibility between Zeus and Xena as mentioned above. That is, the eigenbasis $|heads\rangle – |tails\rangle$ and $|heads\rangle + |tails\rangle$ makes no sense and without that understanding, it is impossible to create a block universe experimental configuration of classical information corresponding to this Hilbert space basis. Now let us continue and show how these inconsistencies play out.

In any given trial of the experiment, since Xena and Yvonne have definite outcomes duly recorded and memorized, there is classical information as to which of the three possible outcomes in Eq. (\ref{Eq13}) was actually instantiated, i.e., Xena obtained heads and Yvonne obtained –1, Xena obtained tails and Yvonne obtained +1, or Xena obtained tails and Yvonne obtained –1. But, it is easy to show that this classical information is not consistent with the entangled state $|\Psi\rangle$. Essentially, as Bub points out [10], this is just to say that ignorance about classical information does not constitute a quantum system. In Bub’s language, classical information is Boolean while quantum information is non-Boolean.

Suppose Zeus measures $\hat{z}$ and obtains OK (eigenvalue for $|OK\rangle_Z$), which can certainly happen since Xena measured either heads or tails. In other words, since we are assuming $|\Psi\rangle$ is the quantum state being measured by Zeus and Wigner for any of the definite configurations for Xena and Yvonne, and the projection of $|\Psi\rangle$ onto $|OK \rangle_Z$ is non-zero, it must be possible for Zeus to obtain OK for a $\hat{z}$ measurement for any prior definite configuration for Xena and Yvonne, i.e., each of the three individual possibilities of heads and –1 and tails and +1 and tails and –1 is compatible with an OK outcome for Zeus’s $\hat{z}$ measurement. But when Zeus obtains OK, Wigner must obtain +1 for a $\hat{y}$ measurement, since $\langle\Psi\mid OK\rangle_Z = -\frac{1}{\sqrt{6}}\langle +|$, which rules out the possibility that the prior configuration of Xena and Yvonne was heads and –1 or tails and –1, respectively, and that contradicts our assumption that $|\Psi\rangle$ is the quantum state for Zeus and Wigner for any of the definite configurations for Xena and Yvonne prior to Zeus and Wigner’s measurements. So, how does Zeus’s OK outcome force Wigner’s $\hat{y}$ measurement to be +? QM interference of course. You  can see that by rewriting Eq. (\ref{Eq13}) as

\begin{equation} |\Psi \rangle = \frac{1}{\sqrt{3}}\left(\sqrt{2}|fail \rangle_Z | – \rangle + |tails \rangle | +\rangle \right)\label{Bub1}\end{equation}

Likewise, suppose Wigner first measures $\hat{w}$ and obtains OK (eigenvalue for $|OK\rangle_Y$), which can certainly happen since Yvonne measured either +1 or –1, i.e., each of the three individual possibilities of heads and –1 and tails and +1 and tails and –1 is compatible with an OK outcome for Wigner’s $\hat{w}$ measurement. But when Wigner obtains OK, Zeus must obtain heads if he measures $\hat{x}$, since $\langle\Psi\mid OK\rangle_Y = -\frac{1}{\sqrt{6}}\langle heads|$, which rules out tails and +1 and tails and –1 as possible prior configurations for Xena and Yvonne, respectively, contrary to our assumption. Again, QM interference is at work, which you can see by rewriting Eq. (\ref{Eq13}) as

\begin{equation} |\Psi \rangle = \frac{1}{\sqrt{3}}\left(| heads \rangle | – \rangle + | tails \rangle |fail \rangle_W \right)\label{Bub2}\end{equation}

Now let me show explicitly what kind of shared, self-inconsistent classical information can result for the inconsistent assumptions involved in this subjective-collapse experiment.

Suppose Xena measures the state

\begin{equation} \frac{1}{\sqrt{2}}\left(| heads \rangle + | tails \rangle \right) \label{Xena}\end{equation}

in the basis $| heads \rangle, | tails \rangle$. Further, suppose that if Xena obtains heads, she sends the state $| heads \rangle$ to Wigner who likewise does a measurement in the basis $| heads \rangle, | tails \rangle$. Conversely, if Xena measures tails, she sends the state $| tails \rangle$ to Wigner who again does a measurement in the basis $| heads \rangle, | tails \rangle$. This constitutes sending classical information of course, which is essentially what is done in FR’s approach. Now, Zeus passes Xena and her lab through a `heads-tails polarizer’ $\left(| heads \rangle + | tails \rangle \right)$ and then does a measurement in the the basis $| heads \rangle, | tails \rangle$. Of course, it is entirely possible that Zeus’s final measurement will yield tails. Keep in mind that Zeus’s outcome is classical information about Xena’s entire recorded history to include Xena’s memories of the entire process. Therefore, Xena’s records and memories will show that she measured tails and sent $| tails \rangle$ to Wigner. Consequently, Wigner must have a classically written record of tails for his outcome. But, of course, Wigner’s classical information is heads, so we do not have a self-consistent collection of classical information being shared between Xena, Zeus, and Wigner. BW call this a “scientific contradiction” and state that it “must not arise for a scientific theory.” I agree of course, so how would the standard formalism of QM deal with this?

In the standard formalism per BW, everyone agrees that all measurements produce a collapse, i.e., measurement update is objective. Therefore, Xena and Yvonne’s measurement outcomes constitute classical information that cannot be treated quantum mechanically if it is going to be shared as part of the block universe. [Of course, one could argue that “unshared classical information” is an oxymoron, but that is a semantical point with ontological implications that I won’t engage here.] Recall, a screened-off system is not part of the block universe/objective reality by definition. Therefore, the exchanges needed in FR to create the inconsistencies are the cause of the inconsistencies. This is where the constraint-based explanation I introduced in my previous Insights, e.g., Blockworld and its Foundational Implications: Delayed Choice and No Counterfactual Definiteness, and book [11] would stand, since all shared classical information is to be represented in the block universe in self-consistent fashion. However, that does not mean we cannot screen off an entire lab and then treat it quantum mechanically. It is simply the case that the screened-off lab cannot interact with the universe, since that creates the possibility of inconsistent, shared classical information in the block universe which constitutes a scientific contradiction. What does the relative-state formalism say?

In the Bohmian account (a relative-state formalism) of FR, Lazarovici & Hubert write [8]

the macroscopic quantum measurements performed by [Zeus] and [Wigner] are so invasive that they can change the actual state of the respective laboratory, including the records and memories (brain states) of the experimentalists in it.

Per Lazarovici & Hubert memories and records change, but the history of those memories and records (along their worldlines prior to measurement) remain intact, so nothing in the past is changed. It’s analogous to passing vertically polarized light through a polarizer at $45^0$ then measuring it horizontally. The light incident on the first polarizer at $45^0$ has no horizontal component, but it does after passing through the polarizer at $45^0$. Consequently, it can now pass through the horizontal polarizer. Thus, for the photons that are now passing through the horizontal polarizer, the polarizer at $45^0$ can be said to have changed them from vertically polarized to horizontally polarized. Likewise, Zeus and Wigner’s $\hat{z}$ and $\hat{w}$ measurements can literally change Xena and Yvonne’s records and memories of their $\hat{x}$ and $\hat{y}$ measurement outcomes.

This does not necessarily constitute scientific contradiction. If Xena and Yvonne’s classical information prior to being measured by Zeus and Wigner is not shared, and the classical information that exists at the end of the experiment that is shared by all participants is not self-contradictory, then there is no scientific contradiction. Of course, it may be impossible to tell a self-consistent dynamical story about how the initial self-consistent set of classical information evolved into the final self-consistent collection of classical information, but again that is not a problem for constraint-based explanation.

Healey also formulates a relative-state approach to FR, which we might infer from post #5275 in Workshop on Wigner’s Friend 2018:

So one could argue that whatever Wigner says about his outcome (more carefully, whatever Zeus measures Wigner’s outcome to be) is not a reliable guide to Wigner’s actual outcome. In particular, even if Zeus takes Wigner’s outcome to have been OK (because that’s what he observes it to be in a hypothetical future measurement on W) Wigner’s actual outcome might equally well have been FAIL.

That is, Zeus and Wigner’s outcomes for measurements on Xena and Yvonne’s records can contradict those records. This violates BW and FR’s assumption of consistency only if you subscribe to the belief that QM probabilities apply to an objective reality. Healey [9] and other relative-state approaches simply deny that assumption. Per Healey’s pragmatic account of QM [9], the job of QM is simply to provide the probabilities/correlations for outcomes in a quantum experiment given the experimental context for each observer, i.e., QM is not providing a physical model or interpretation of what happens between experimental initiation and termination — in Bub’s wording, “the non-Boolean link” between the Boolean initial conditions and the Boolean outcomes.

Assuming the existence of a true quantum system $|\Psi\rangle$ represented by Eq. (\ref{Eq13}) and the standard formalism, Wigner and Zeus share a common classical context for making their measurements of $|\Psi\rangle$. In the relative-state formalism, Wigner/Zeus must treat Zeus/Wigner as a third quantum system resulting in a new version of Eq. (\ref{Eq13}) if Zeus/Wigner makes his measurement first. In the standard theory, Eq. (\ref{Eq13}) is used by both Zeus and Wigner to determine distributions in their common spacetime context for whatever measurements they decide to make, since their measurements act on different parts of $|\Psi\rangle$. Thus, the order of their measurements does not affect the predicted probabilities. For example, regardless of what Zeus measures, the probability that Wigner will get an OK outcome for a $\hat{w}$ measurement if Xena got tails in her $\hat{x}$ measurement is zero. That’s because the tails part of Eq. (\ref{Eq13}) is

\begin{equation} \frac{1}{\sqrt{3}}| tails \rangle |fail \rangle_W\label{Bub3}\end{equation}

and $|fail \rangle_W$ is orthogonal to $|OK \rangle_W$. But, in the relative-state formalism, this same probability depends on whether or not Zeus makes his measurement first and what measurement Zeus makes, since the functional form of $|\Psi\rangle$ will be different for Wigner if Zeus makes an intervening measurement.

For example, suppose Zeus measures $\hat{x}$ first. After Zeus’s measurement per the relative-state formalism, Eq. (\ref{Eq13}) reads

\begin{equation} |\Psi \rangle = \frac{1}{\sqrt{3}}\left(| heads \rangle_X | heads \rangle_Z | – \rangle + | tails \rangle_X | tails \rangle_Z |fail \rangle_W \right)\label{Bub4}\end{equation}

[Notice we must now distinguish Xena from Zeus even though they’re measuring the same thing. The same must be done with Yvonne and Wigner.] In this case, as in the standard theory, the probability that Wigner will get an OK outcome for a $\hat{w}$ measurement if Xena got tails in her $\hat{x}$ measurement is zero because the tails part of Eq. (\ref{Bub4}) is

\begin{equation} \frac{1}{\sqrt{3}}| tails \rangle_X | tails \rangle_Z |fail \rangle_W\label{Bub5}\end{equation}

after Zeus’s $\hat{x}$ measurement. But, suppose Zeus makes a $\hat{z}$ measurement instead. To use the relative-state formalism, we must first cast Eq. (\ref{Eq13}) in the OK-fail basis as [10]

\begin{equation} |\Psi \rangle = \frac{1}{\sqrt{12}}| OK \rangle_X | OK \rangle_Y – \frac{1}{\sqrt{12}}| OK \rangle_X | fail \rangle_Y + \frac{1}{\sqrt{12}}| fail \rangle_X | OK \rangle_Y + \frac{\sqrt{3}}{2}| fail \rangle_X | fail \rangle_Y\label{BubEq16}\end{equation}

Now, after Zeus makes his $\hat{z}$ measurement, Eq. (\ref{BubEq16}) reads [10]

\begin{equation}
\begin{split}
|\Psi \rangle = &\frac{1}{\sqrt{12}}| OK \rangle_X | OK \rangle_Z | OK \rangle_Y – \frac{1}{\sqrt{12}}| OK \rangle_X | OK \rangle_Z | fail \rangle_Y +\\& \frac{1}{\sqrt{12}}| fail \rangle_X | fail \rangle_Z | OK \rangle_Y + \frac{\sqrt{3}}{2}| fail \rangle_X | fail \rangle_Z | fail \rangle_Y
\end{split}
\label{BubEq17}\end{equation}

Now if you undo Xena’s $| OK \rangle_X$ and $| fail \rangle_X$ in terms of $|heads\rangle_X$ and $|tails \rangle_X$ in Eq. (\ref{BubEq17}), the tails part is [8]

\begin{equation}
|tails \rangle_X\left[ \frac{\sqrt{5}}{\sqrt{12}}\left(\frac{3}{\sqrt{10}}| fail \rangle_Z + \frac{1}{\sqrt{10}}| OK \rangle_Z \right)|fail \rangle_Y + \frac{1}{\sqrt{12}}\left(\frac{1}{\sqrt{2}}| fail \rangle_Z – \frac{1}{\sqrt{2}} | OK \rangle_Z \right) | OK \rangle_Y\right]
\label{BubEq18}\end{equation}

And since

\begin{equation}
\left(\frac{1}{\sqrt{2}}| fail \rangle_Z – \frac{1}{\sqrt{2}} | OK \rangle_Z \right) | OK \rangle_Y = |tails\rangle_Z | OK \rangle_Y
\label{BubEq20}\end{equation}

we now have a non-zero probability for Wigner obtaining an OK outcome for a $\hat{w}$ measurement when Xena obtains a tails outcome for her $\hat{x}$ measurement (it’s $\frac{1}{6}$ actually [10]). If Zeus doesn’t make a measurement, Eq. (\ref{BubEq16}) becomes

\begin{equation}
\begin{split}
|\Psi \rangle = &\frac{1}{\sqrt{12}}| OK \rangle_X | OK \rangle_Y | OK \rangle_W – \frac{1}{\sqrt{12}}| OK \rangle_X | fail \rangle_Y | fail \rangle_W +\\& \frac{1}{\sqrt{12}}| fail \rangle_X | OK \rangle_Y | OK \rangle_W + \frac{\sqrt{3}}{2}| fail \rangle_X | fail \rangle_Y | fail \rangle_W
\end{split}
\label{BubEqX}\end{equation}

after Wigner’s $\hat{w}$ measurement. The $|OK\rangle_W$ part of this is

\begin{equation}
\frac{1}{\sqrt{12}}\left(| OK \rangle_X  + | fail \rangle_X \right) | OK \rangle_Y | OK \rangle_W = \frac{1}{\sqrt{6}} | heads \rangle_X | OK \rangle_Y | OK \rangle_W
\label{BubEqXX}\end{equation}

which has no tails piece for Xena, so the probability of Wigner obtaining an OK outcome for a $\hat{w}$ measurement when Zeus hasn’t made a measurement and when Xena obtains a tails outcome for her $\hat{x}$ measurement is again zero.

You can see why Zeus’s intervening $\hat{z}$ measurement per the relative-state formalism can cause possible contradictions between records or changes to records and memories in the Wigner’s friend scenario. In the relative-state formalism, Zeus’s measurement outcome must match Xena’s hypothetical or recorded measurement outcome in the basis used by Zeus, e.g.,  $| OK \rangle_X  | OK \rangle_Z$. Everything is fine as long as Zeus and Xena make the same measurement, but if Zeus measures in a rotated Hilbert space basis relative to Xena, his possible measurement outcomes will contain cross terms in Xena’s possible measurement outcomes, e.g., $| heads \rangle_X  | tails \rangle_Z$ and $| tails \rangle_X  | heads \rangle_Z$, which implies a contradiction between what Zeus measures for Xena’s measurement outcomes and what Xena actually measured and recorded. Such contradictions in shared classical information cannot occur in the block universe (by definition) or any model of objective reality. But, in this relative-state approach, QM does not provide classical information to be housed in objective reality, it only provides classical information relative to each observer.

In September 2020, Bong et al. published “A strong no-go theorem on the Wigner’s friend paradox,” and claimed to have a “proof-of-principle” experiment for these so-called “extended Wigner’s friend scenarios” (EWFS) [12]. Specifically, they derive an inequality that when violated by any physical theory entails the violation of at least one of the following assumptions in the context of EWFS (worded colloquially here by Cavalcanti) [13]:

1. When someone observes an event happening, it really happened.
2. It is possible to make free choices, or at least, statistically random choices.
3. A choice made in one place can’t instantly affect a distant event.

They refer to these assumptions collectively as Local Friendliness (LF). Their LF theorem is:

If a superobserver [Wigner or Zeus above] can perform arbitrary quantum operations on an observer and its environment [Xena or Yvonne above], then no physical theory can satisfy Local Friendliness.

Assumption 1 is the “Absoluteness of Observed Events (AOE)): An observed event is a real single event, and not relative to anything or anyone.” As they point out, this is a tacit assumption made in deriving Bell inequalities, e.g., the CHSH inequality. And as I explained above, this assumption is necessary for using the formalism of QM, i.e., if one violates this assumption when using the formalism of QM, contradictions and absurdities can arise. So, while it may certainly be true that violating Assumption 1 leads to the violation of their LF inequality, one cannot use QM to check their LF inequality while violating Assumption 1. That means a violation of their LF inequality by QM entails the violation of either or both of “Assumption 2 (No-Superdeterminism (NSD)): Any set of events on a space-like hypersurface is uncorrelated with any set of freely chosen actions subsequent to that space-like hypersurface” or “Assumption 3 (Locality (L)): The probability of an observable event e is unchanged by conditioning on a space-like-separated free choice z, even if it is already conditioned on other events not in the future light-cone of z.” Of course, NSD and L are just the assumptions for the Bell inequality, so other than an new inequality nothing new has been introduced in this paper regarding QM.

As with Proietti et al., the spacetime region for the Bong et al. experiment resides entirely in the block universe of self-consistent, shared classical information, so we can use QM to check their experiment for the violation of their LF inequality. Again, if the LF inequality is violated by QM (as it is for this experiment), we only know that we must abandon NSD or L, since AOE is required to map the QM formalism to experimental arrangements. In this experiment, the “superobservers” are Alice and Bob and their friends are Charlie and Debbie, respectively. No measurement outcomes for Charlie and Debbie are involved in the LF inequality, so we may dismiss them immediately; again, this is certainly not an EWFS (which they readily admit in the paper). Their source produces a mixture that they can tune via $\mu$
\begin{equation}
\rho_\mu = \mu |\Phi^- \rangle \langle \Phi^-| + \frac{1-\mu}{2} (|HV\rangle \langle HV| + |VH\rangle \langle VH| )
\end{equation}
where $|\Phi^- \rangle$ is the spin singlet state. They find the maximum violations of the Bell and LF inequalities occur when the state is tuned entirely to the spin singlet state ($\mu = 1$), so I’ll briefly review that case.

Alice and Bob choose between three spin measurements labeled $\{A_1,A_2,A_3\}$ and $\{B_1,B_2,B_3\}$, respectively, in each trial of the experiment as shown schematically in Figures 1 & 2. In the context of these measurements, the LF inequality is
\begin{equation}
-\langle A_1 \rangle – \langle A_2 \rangle – \langle B_1 \rangle – \langle B_2 \rangle – \langle A_1B_1 \rangle – 2\langle A_1B_2 \rangle – 2\langle A_2B_1 \rangle + 2\langle A_2B_2 \rangle – \langle A_2B_3 \rangle – \langle A_3B_2 \rangle – \langle A_3B_3 \rangle -6 \le 0
\end{equation}
By comparison, the CHSH (Bell) inequality for these measurements is
\begin{equation}
\langle A_2B_2 \rangle – \langle A_2B_3 \rangle – \langle A_3B_2 \rangle – \langle A_3B_3 \rangle -2 \le 0
\end{equation}
These inequalities are saturated for the counterfactually definite set $\{A_1,A_2,A_3,B_1,B_2,B_3\} = \{1,-1,1,-1,-1,-1\}$, for example. In order to evaluate them for the spin singlet state, we choose the measurements shown in Figure 3. These choices are close enough to those used by Bong et al. so as to reproduce their results within experimental error. For the spin singlet state we have $\langle A_i \rangle = \langle B_j \rangle = 0$ and $\langle A_iB_j \rangle = -\cos\theta$ where $\theta$ is the angle between the measurements $A_i$ and $B_j$ as shown in Figure 3 [14 or this Insight]. With these measurements of the spin singlet state the lefthand sides of the LF inequality and the CHSH (Bell) inequality are both 0.5, in agreement with the Bong et al. results.

In previous Insights, I have shown how the ant’s-eye view creates consistency paradoxes for closed timelike curves and inexplicable initial conditions in Big Bang cosmology that were resolved by the block universe view with Einstein’s equations acting as the 4D constraint. Then I showed how the ant’s-eye view creates conundrums associated with entanglement, e.g., the GHZ experiment, the quantum liar experiment, and the DFBV experiment, that were resolved by taking the “all-at-once view” of QM with the Feynman path integral acting as the 4D constraint. In all these cases, the block universe view easily resolved the mysteries via 4D-constraint-based explanation that were created by the ant’s-eye view via dynamical/causal explanation. Indeed, I then showed how a 4D constraint plus the block universe view (conservation per no preferred reference frame) can be very compelling even when there is no consensus dynamical counterpart for the ant’s-eye view at all — conservation of binary information to explain the Tsirelson bound and the unreasonable effectiveness of the Popescu-Rohrlich correlations and conservation of angular momentum on average to resolve the mystery of the Mermin device [14]. So, it should not be at all surprising that we can understand the quantum mystery called Wigner’s friend as yet another “faux mystery” created by ignoring 4D constraints in the block universe view. This is just another case where physics seems to be admonishing us to rise to Wilczek’s challenge and think as heptapods or Tralfamadorians instead of ants [11].

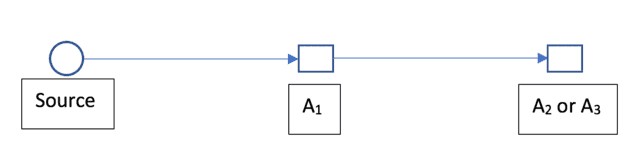
Figure 1. Alice’s side of Bong et al. experiment. Bob’s side is the same with $B_j$ replacing the $A_i$.

 

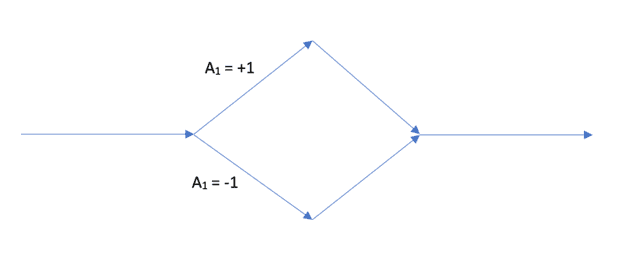
Figure 2. If the measurement $A_1$ is done, the particle is intercepted on the upper path ($A_1 = +1$) or the lower path ($A_1 = -1$). Otherwise, the particle is allowed to continue to either an $A_2$ or $A_3$ measurement. In order to promote this to a “proof-of-principle” EWFS experiment, the path inside here is taken to represent Charlie (Debbie on Bob’s side) having made his(her) measurement and obtained his(her) result.

 

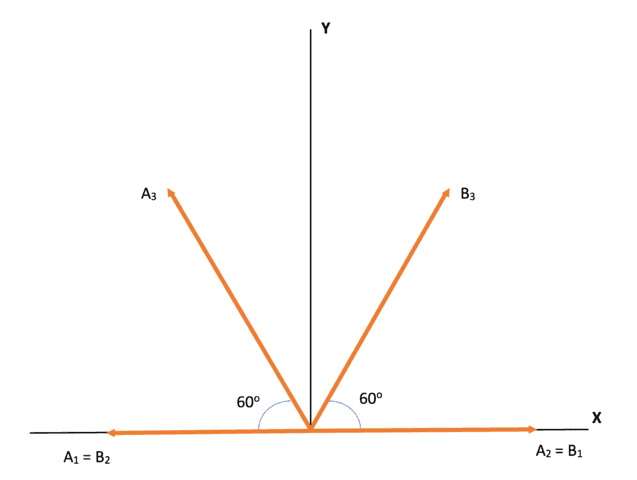
Figure 3. Spin measurements $A_i$ and $B_j$ in the xy plane.

References

1. Healey, R. ( 2018). Quantum Theory and the Limits of Objectivity. Foundations of Physics 48(11), 1568–1589.
2. Frauchiger, D. and Renner, R. (2018). Quantum theory cannot consistently describe the use of itself. Nature Communications 9(1), 3711.
3. Wigner, E. (1961). Remarks on the mind-body question. In I. J. Good (ed.), The Scientist Speculates. Heineman. pp. 284–302.
4. Bartlett, S.D., Rudolph, T., and Spekkens, R.W. (2007). Reference frames, superselection rules, and quantum information. Reviews of Modern Physics79, 555 https://arxiv.org/abs/quant-ph/0610030.
5. Proietti, M., Pickson, A., Graffitti, F., Barrow, P., Kundys, D., Branciard, C., Ringbauer, M., and Fedrizzi, A. (2019). Experimental rejection of observer-independence in the quantum world.
6. Silberstein, M., and Stuckey, W.M. (2019). Quantum Mechanics and the Consistency of Conscious Experience.
7. Baumann, V. and Wolf, S. (2018). On Formalisms and Interpretations. Quantum 2, October, 99.
8. Lazarovici, D. and Hubert, M. (2018). How Quantum Mechanics can consistently describe the use of itself.
9. Healey, R. (2017). The Quantum Revolution in Philosophy. Oxford University Press.
10. Bub, J. (2019). `Two Dogmas’ Redux. Forthcoming in a volume honoring Itamar Pitowsky, edited by Orly Shenker and Meir Hemmo. https://arxiv.org/abs/1907.06240
11. Silberstein, M., Stuckey, W.M. and McDevitt, T. (2018). Beyond the Dynamical Universe. Oxford University Press, p. 12.
12. Bong, K., Utreras-Alarc ́on, A., Ghafari, F., Liang, Y., Tischler, N., Cavalcanti, E., Pryde, G., and Wiseman, H. (2020). A strong no-go theorem on the Wigner’s friend paradox. Nature Physics. https://doi.org/10.1038/s41567-020-0990-x.
13. Cavalcanti, E. (2020). A new quantum paradox throws the foundations of observed reality into question. The Conversation. https://theconversation.com/a-new-quantum-paradox-throws-the-foundations-of-observed-reality-into-question-144426.
14. Stuckey, W.M., Silberstein, M., McDevitt, T., and Le, T.D. (2020). Answering Mermin’s challenge with conservation per no preferred reference frame. Scientific Reports 10, 15771.