Frames of Reference: A Skateboarder’s View

My essay Explaining Rolling Motion raised some commentary about frames of reference and their equivalence when solving physics problems. I wish to pursue the idea of shifting one’s frame of reference because its use is relatively uncommon in introductory physics courses.   Students are asked to solve problems mostly in the (approximately) inertial frame of the Earth at the risk of putting their thinking into a “box”.  Notable exceptions are relative motion at constant velocity and the use of the center of mass frame in treating collisions.  I believe that more physical situations need to be explored to encourage students to think out of the box.  In this essay, I present an early attempt to do just that and what I learned from it.  I start with a well-known problem to provide a reference point for what follows.   I close with a historical perspective and a few afterthoughts.  As can be inferred from the title, part II is contemplated and already in the works.

The problem (an old standard)

A small block is released from rest at the top of a frictionless non-planar incline. It slides down left to right until it reaches a horizontal surface and coasts to the right thereafter. Neglecting air resistance, find the final speed of the block at the bottom of the incline given the vertical drop h.

Solution

We use mechanical energy conservation between two points, the top and the bottom of the incline. We assume that zero gravitational is at the bottom of the incline.

At the top:  $K_i = 0;  U_i = mgh$.    At the bottom:  $K_f = \frac{1}{2}mv^2;  U_f = 0$.

By conservation of mechanical energy, $\Delta K +\Delta U=0$.  Then,

$$ \left(  \frac{1}{2}mv^2-0 \right)+(0-mgh)=0 \rightarrow v=\sqrt{2gh}  $$.

The twist

Now consider the reference frame of a skateboarder who is moving to the right with speed $u= \sqrt{2gh}$.  Redo the problem in the skateboarder’s frame of reference to find the block’s initial speed, v₀, given the vertical drop h.

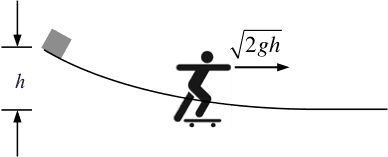
We note that at the bottom of the incline the block is at rest in the skateboarder’s (primed) frame and conserve mechanical energy once more.

At the top:  $K’_i = \frac{1}{2}m(-v_0)^2;  U’_i = mgh$.    At the bottom:  $K’_f = 0;  U’_f = 0$.

By conservation of mechanical energy, $\Delta K’ +\Delta U’=0$.  Then,

$$ \left( 0- \frac{1}{2}mv_0^2 \right)+(0-mgh)=0   $$

$$ – \frac{1}{2}mv_0^2 -mgh=0   \rightarrow ???  $$

We have reached the impossibility of having, on the left-hand side, the sum of two negative numbers that must be zero according to the right-hand side.  Something is amiss.  At this point I ask you, the reader, to please pause, consider your reaction to what you just read, answer the three-choice question below and continue reading if you wish.

How can this situation be resolved?

1. Mechanical energy must not conserved in the skateboarder’s frame.
2. Mechanical energy is always conserved; there must be an algebraic error in the derivation.
3. Mechanical energy is always conserved, this is a trick question.

Note:  The original article had a readers’ poll which was removed upon expiration.

The resolution

A savvy skateboarder would realize that mechanical energy (ME) is not conserved in the moving frame.  In the lab frame, the normal force is always perpendicular to the block’s displacement and does zero work on the block.  In the skateboarder frame, the path of the block is no longer perpendicular to the normal force.
In fact, the skateboarder sees the block’s speed start at some initial non-zero value and then drop to zero and remain zero as if a dissipative force stopped it. Therefore, ME is not conserved in the moving frame and 1 is the correct answer.
Instead of ME conservation, the skateboarder would be well advised to use the work-energy theorem and take into account the work done by the normal force.
OK, but if you were the skateboarder, how would you calculate this work considering the arbitrary curvature of the incline? The answer is by transforming to the lab frame in which the normal force does no work. Let primes denote quantities in the moving frame. Using $\vec{u}$ as the relative velocity between the two frames, we have $\vec{r}’=\vec{r}-\vec{u}~t$.  Then $d \vec{r}’=d\vec{r}-\vec{u}~dt$.  The work done by any force in the primed frame is

$$W’=\int \vec{F} \cdot d \vec{r}’ =\int \vec{F} \cdot (d \vec{r} -\vec{u}~dt)=\int \vec{F} \cdot d \vec{r} -\vec{u} \cdot \int \vec{F}~dt$$

The first term in the right is the work done by the force in the unprimed frame while the second term is $-\vec{u} \cdot \vec{J}$ where $\vec{J}$ is the frame-independent impulse delivered to the system. Thus, the work done by the normal force in the primed frame is,

$${W’}_N=W_N-\vec{u} \cdot \vec{J}=W_N-m\vec{u} \cdot \Delta \vec{v}’ $$

In this case, $W_N$ is zero. The skateboarder sees the incline move with constant velocity $-\vec{u}$ and, since the block is initially at rest relative to the incline, the skateboarder deduces that $\vec{u}=v_0 \hat{x}$.   Furthermore, according to the skateboarder  $\Delta \vec{v}’=+v_0 \hat{x}$ because the block is initially moving to the left with speed $v_0$ and finally comes to rest.  Thus,

$${W’}_N=-m (v_0 \hat{x}) \cdot \left(  v_0 \hat{x} \right) =-mv_0^2$$

According to the work-energy theorem

$$\Delta (ME’)={W’}_N$$

We already have the left side of the equation from the earlier attempt to solve this in the primed frame.  Thus,

$$ – \frac{1}{2}mv_0^2 -mgh=-mv_0^2 $$

From this, it is easy to show that $v_0=\sqrt{2gh}$.

A second opinion

The skateboarder can sidestep the question of how to account for the work done by the normal force in the primed frame by using combined conservation of mechanical energy and linear momentum.  Consider a two-component system with component A of mass $m_A$ being the block and component B with mass $m_B$ the Earth + incline. In this case, mechanical energy is indeed conserved because the work done by the incline on the block is the negative of the work done by the block on the incline while there is no friction to dissipate energy. In the primed frame, both systems are initially moving to the left with speed $v_0$.  When the block reaches the bottom of the incline, it is at rest while Earth + incline are moving to the left with speed $v’_f$.  We have then

$$-m_Av_0-m_Bv_0=0-m_Bv’_f$$

$$m_Agh+\frac{1}{2}(m_A+m_B)v_0^2=\frac {1}{2}m_B{v’}_f^2$$

This is a system of two equations and two unknowns that is solved to give

$$ v_0=\sqrt{ \frac{2gh}{1+m_A/m_B}};~~~v’_f=\sqrt{2(1+m_A/m_B)gh}$$

When  $m_A/m_B <<1$, to a very good approximation, $v_0 = v’_f = \sqrt{2gh}$ which is consistent with the results in the previous section.  It should be clear to the reader that in either reference frame momentum and energy conservation gives the exact solution while energy conservation only results in an approximation, albeit a good one.

Historical background and afterthoughts

In my early days of teaching, I had time left at the end of a lecture on mechanical energy conservation. Instead of dismissing the class early, I thought up the skateboarder question on the fly to illustrate that the laws of physics are invariant when viewed from a different inertial frame. I was surprised and embarrassed to discover (with 3 minutes left in the period) that things literally didn’t add up. Feeling the pressure, I dismissed the class promising a resolution next time. In retrospect, asking this question was an act of faith, affirming my belief in the invariance of mechanical energy conservation under the Galilean transformation.  Moral: Don’t start something unless you have already established how it will play out.

This experience not only chastised me but also made me wonder whether others shared the same blind spot. I asked undergraduates, graduate students, and colleagues the three-choice question with mixed results.  It appears that the belief in mechanical energy conservation is quite robust among students.  A few of them sacrificed mathematical rigor on the altar of mechanical energy conservation blithely asserting that $(-v_0)^2 = -v_0^2$.  My colleagues’ reactions generally varied from the non-committal “I am busy now, let me take it home with me and I’ll get back to you”  to the indignant “Is this a gotcha question?” Only one person was quick to point out the momentum conservation approach.

Some confusion arises partly because the principle of mechanical energy conservation is often formulated improperly in textbooks and on the internet.  For example, the current Wikipedia entry states, “The principle of conservation of mechanical energy states that in an isolated system that is only subject to conservative forces the mechanical energy is constant.”   A better formulation, which allows the presence of non-conservative forces as long as they do no work, might be “The principle of conservation of mechanical energy states that, in an isolated system on which only conservative forces do work, the mechanical energy is constant.”

I have assiduously avoided labeling the surface contact force as either conservative or non-conservative.  On one hand, it could be argued that it is electromagnetic in origin, therefore it can be derived, at least in principle, from a potential. Furthermore, the normal component can be viewed as a conservative spring-like elastic force.  On the other hand, if a book is dropped on a table, the book quickly loses its mechanical energy and comes to rest as a result of the same normal force acting on it.  So which is it?  Conservative or non-conservative?  Contact forces are unique in that they necessarily introduce lattice vibrations, that dissipate energy into the lattice.  When an object is dropped on a flat surface, there is some ringing which is relatively quickly damped out as all the mechanical energy is dissipated by the lattice vibrations.  Similar considerations apply when an object is dragged across the surface.  While contact forces are in principle conservative, in practice they unavoidably dissipate mechanical energy by converting some of it into internal energy.  Thus, when contact forces are present, the boundary between the work-energy theorem and the first law of thermodynamics becomes blurred.