Acoustic ‘beats’ from Mismatched Musical Frequencies

Introduction

In late high school physics courses and first-year university courses, the phenomenon of acoustical ‘beats’ (digital audio) is often covered. This is an interesting phenomenon, but it is usually only skated over, leaving the students with not much more than a feeling that the beats somehow arise from the two waves moving in and out of sync over time, thereby generating constructive and destructive interference. That creates the ‘beats’ effect which is, in a very loose sense, the acoustic analog of the striped interference pattern seen in a double-slit experiment. The attentive student will come away from such instruction remembering that the frequency of the beats is equal to the difference of the two frequencies, but not much more. This short note aims to present a mathematical explanation of the phenomenon and to observe some of the consequences of the analysis.

Acoustic ‘beats’

Imagine two pure musical tones being played which, observed at a particular point in space give pressure variations (relative to ambient pressure) over time according to the equations:
\begin{equation}P1(t)=\cos (2\pi f_1 t);\ \ P2(t)=\cos (2\pi f_2 t)\end{equation}
The volumes of these waves are the same, the frequencies in Hertz (cycles per second) are ${f_1}$ and ${f_2}$ respectively, and we assume $f_1>f_2$. The ‘periods’, which are the times taken for a full cycle of pressure variation, are $T_1=1/{f_1}$ and $T_2=1/{f_2}$.

At the observation location, the observed pressure variation is the sum of these two pressure functions:
\begin{equation}P_{tot}(t)=\cos (2\pi f_1 t)+\cos (2\pi f_2 t) \end{equation}

We call the argument to the cosine function the ‘phase’ of the wave. The difference between the two phases is called the ‘phase difference’, and it is that which is crucial in understanding beats. We say that the two waves are synchronized at time $t$ (‘in sync’) if the phase difference is a multiple of $2\pi$. That means that the two waves are at the same point in their respective cycles, eg both at a maximum, both at a minimum, both crossing the horizontal axis in an upward direction, etc. At a time when the two waves are close to ‘in sync’, their amplitudes add, making the pressure variations approximately double the size of those of each wave. That makes the sound louder.

Conversely, when the phase difference is a half-cycle, the pressure variation contributed by one wave will be the negative of that contributed by the other. So the addition will cause them to cancel, and the amplitude of the pressure variations will be close to zero. That makes the sound quieter.

At least, that’s the general idea. Now let’s examine how mathematics works.

The Mathematics of Acoustic ‘beats’

The waves start off in sync at time 0. Then they will be in sync again at all times $t$ such that
\begin{equation}t=a\,{T_2} =(a+k)\,T1 \end{equation}
for integer $k$. The real number $a$ is the number of ${T_2}$ cycles elapsed at time $t$. Solving the equation for $a$ gives $a=k\frac{T1}{{T_2}-T1}$. Setting $k$ equal to 1, we see that the time between successive synchronizations (the ‘synchronization period’) is:
\begin{equation}T_{sync}\equiv \frac{T1\,{T_2}}{{T_2}-T1}=\frac{1}{1/T1-1/{T_2}}=\frac{1}{{f_1}-{f_2}} \end{equation}
The frequency $f_{sync}$ of synchronizations is the reciprocal of that period, which is ${f_1}-{f_2}$. Around the time of synchronization, the amplitude of the combined wave is close to double that of the component waves. That high amplitude lasts for as long as the waves are approximately synchronized, and the phenomenon recurs every $T_{sync}$ seconds, generating a surge of volume that we call a ‘beat’, around each synchronization time.

Consider what would happen if we played two tones with frequencies of 50 Hz and 55 Hz which are, by the way, respectively the second lowest ‘A’ on a standard piano and the hum made by an electrical transformer. We would hear five ‘beats’ per second, as $55-50=5$. If the frequencies were 50 Hz and 51 Hz we would hear only one beat per second. If they were 49 Hz and 54 Hz we would again hear five beats per second.

This is what the waveform of the 50 Hz vs 51 Hz pair looks like. The height of the blue line above the horizontal line shows the variation over time of pressure above and below the ambient pressure.

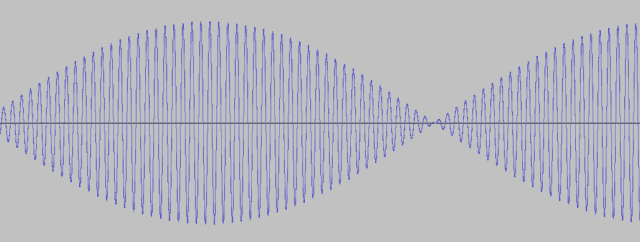
The following sound clip shows what it sounds like.

And here are the two constituent waves. Unless you are exceptionally talented, you will not be able to tell the difference between the 50Hz and the 51Hz wave. It’s hard to believe that two such pure tones generate the strange sound above.

50Hz:

51Hz:

Considered in terms of levels of pressure variation, there is an interesting difference between the cases of 50 vs 55 and 49 vs 54. For the first case, the first beat will occur at the time $t=\frac{1}{5}=\frac{10}{50}=\frac{11}{55}$. That is after 10 and 11 cycles of the lower and higher frequency waves respectively. Further, the synchronization occurs when the phases are an exact multiple of $2\pi$, so that the pressure variation at that time is exactly the sum of the two amplitudes, maximizing the impact.

However, when the waves have frequencies of 49 Hz and 54 Hz, at the time when the first synchronization occurs at 200 ms, the lower tone has completed 9.8 cycles and the higher tone has completed 10.8. So neither is giving a maximum pressure variation. That happens 4 ms later when the higher frequency wave attains its maximum, having completed 11 cycles. But at that point, the waves are slightly out of sync again, so the pressure variation is less than the sum of the amplitudes.

They are not very far out of sync. At 204 ms the lower tone has completed 9.98 cycles, making it one-fiftieth cycle out of sync ($1/50=1/(10-9.98)$), so that the pressure achieved at that time is 1.99 times the individual amplitudes, rather than double. At the next synchronization after that, the lower tone will be two-fiftieth cycles out of sync at its closest maximum to the synchronization point. For the next sync after that, the closest maximum for the higher tone is 0.4 cycles before the sync point. The next is 0.2 cycles before and the next sync after that occurs at a joint maximum. This is shown in the following table.
$$
\begin{vmatrix}
\textit{Sync number      }&0 & 1 & 3 & 3 & 4 & 5\\
\textrm{Sync time (ms)        }&0 & 200 & 400 & 600 & 800 & 1000\\
\textrm{Wave 1 Phase}&0 & 10.8 & 21.6 & 32.4 & 43.2 & 54.0\\
\textrm{Phase adj to closest-}&0 & 0.2 & 0.4 & -0.4 & -0.2 & 0\\
\textrm{wave 1 max}\\
\textrm{Time of closest- }&0 & 204 & 407 & 593 & 796 & 1000\\
\textrm{wave 1 max (ms)}\\
\textrm{Wave 2 height at that time}&1 & 0.99 & 0.97 & 0.97 & 0.99 & 1\\
\textrm{Total pressure variation}&2 & 1.99 & 1.97 & 1.97 & 1.99 & 2
\end{vmatrix}
$$
Looking at the last row of the table, we see that this generates a very small (probably not discernible to the naked ear) cycle of the loudness of the beats, with a period of one second. In general, the discernibility of the variation in loudness will depend on how far away from the maximum the pressure wave of the lower tone is when the higher tone is at the closest maximum to a synchronization time.

To have beats that are constant in volume, we require that, at each synchronization, both waves deliver a maximum pressure variation, which means they must have both completed a whole number of cycles. So we require that, at the first synchronization time $\frac{T1\,T_2}{T_1+T_2}$ we have:
\begin{equation}\frac{T1\,T_2}{T_2-T_1}=mT_1=nT_2 \end{equation}
for integers $m,n$. That is equivalent to requiring that $(T_2-T_1)$ exactly divides $T_2$ (which is true iff it exactly divides $T_1$). Or, expressed in terms of frequencies, this requirement is that $(f_1-f_2)$ exactly divides $f_1$ (and hence also $f_2$).

We call this the ‘level beat requirement’. It will never be satisfied in practice because values in the real world can never be controlled with perfect precision. However, if it is close enough, that is, if $\frac{T_2}{T_2-T_1}$ is close enough to an integer, the beats will be indiscernibly close to level.

Here’s a waveform picture and a sound file of the pair of 50Hz and 55Hz, giving five (almost) perfectly level beats per second:

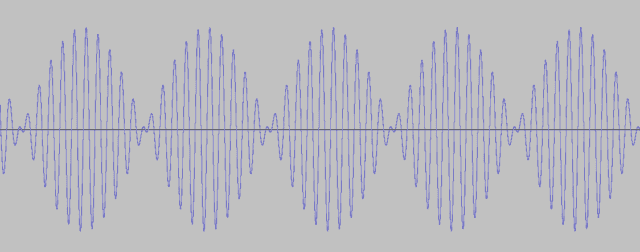
We can develop a rule of thumb for the amount of variation in beat loudness as follows. At any synchronization time, the longest interval from then to the closest (earlier or later) maximum pressure variation of the higher tone is a one-half period of that tone, ie $\frac{T_1}{2}$. Dividing this by $T_{sync}$ gives us an upper bound on how far out of sync the waves can be at that maximum. That is

\begin{equation}\frac12 \frac{T_1}{T_{sync}}=\frac12\cdot T_1\cdot \frac{T_1-T_2}{T_2T_1}=\frac{T_1-T_2}{2T_2}=\frac{f_2-f_1}{2f_1}=\frac{f_{sync}}{2f_1}\end{equation}
The smaller this ratio, the smaller the phase difference at the maxima closest to the synchronization points, and hence the closer the pressure variations at those points will be to twice the amplitudes.

As an example, we mirror the above table of calculations for a new pair of tones at 21 Hz and 26 Hz.
$$
\begin{vmatrix}
\textit{Sync number      }&0 & 1 & 3 & 3 & 4 & 5\\
\textrm{Sync time (ms)        }&0 & 200 & 400 & 600 & 800 & 1000\\
\textrm{Wave 1 Phase}&0 & 5.2 & 10.4&15.6&20.8&26\\
\textrm{Phase adj to closest-}&0 & 0.2 & 0.4 & -0.4 & -0.2 & 0\\
\textrm{wave 1 max}\\
\textrm{Time of closest-}&0 & 192 & 384& 615 & 808 & 1000\\
\textrm{ wave 1 max (ms)}\\
\textrm{Wave 2 height at that time}&1 & 0.97 & 0.89 & 0.89 & 0.97 & 1\\
\textrm{Total pressure variation}&2 & 1.97 & 1.89 & 1.89 & 1.97 & 2
\end{vmatrix}
$$
The variation of maximum pressure is between $[1.89,2]$, compared to a much tighter range of $[1.97,2]$ for the higher pair. This corresponds to the ratio in equation (6) being approximately 0.1 for this pair and 0.05 for the higher pair.

We can estimate the period $T_{var}$ for a cycle of variation of beat loudness as follows. First, we note that in practice there will be no exact cycle because that would require that both $T_1$ and $T_2$ are exact multiples of some shorter period. However, the beat loudness will be approximately the same at two-beat times that are separated by an interval that is almost a whole number of cycles of both waves, that is, where the interval is:
\begin{equation}\Delta t=mT_1=nT_2 \end{equation}
for $m$ an integer and $n$ a number that is close to an integer.

We can set a requirement that starting our interval at $t=0$ so that both waves are in sync at a maximum there, the end of the interval occurs at the earliest time when the higher wave is at a maximum and the lower wave gives a pressure variation greater than $(1-\epsilon)$, where $\epsilon>0$ is a specified tolerance.

With those parameters, we choose $T_{var}$ to be $mT_1$ where $m$ is the lowest positive integer for which $\cos (2\pi mT_1/T_2)>1-\epsilon$. The closer the ratio $\frac{T_1}{T_2}$ is to some rational number with a low denominator, the shorter that period will be. In the idealized case where the frequencies $f_1$ and $f_2$ are both exact integers, we get a perfect cycle of beat variation of length $T_{var}=1/\gcd(f_1,f_2)$, where ‘gcd’ indicates ‘greatest common divisor’.

The two examples shown in the above tables are of this type.

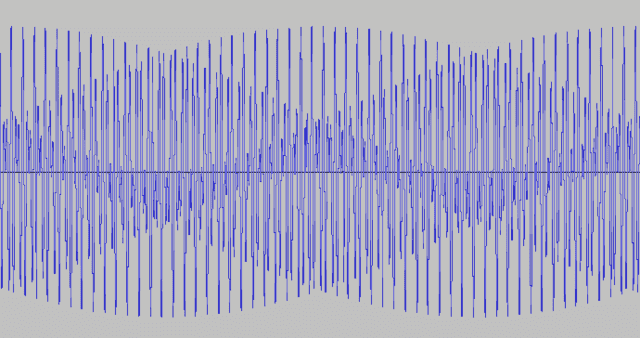
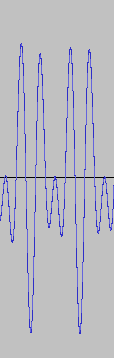
For a pair of tones at 27.5Hz and 41Hz, there are 13.5 beats per second, and the cycle of beat loudness is two seconds, with a range of beat loudness in \([1.54,2\). Here are two pictures of the waveform. The waveform’s first picture covers four seconds, which is two cycles of beat loudness variation. The second picture zooms in on two beats. We see that in this case, each beat consists of only two big maxima with a minimum in between (this compares to the slower beat above in the 50Hz vs 55Hz case, where there were four to five peaks per beat). Between the beats, there are a few small wiggles, where destructive interference is occurring. Even with only two beats shown, we can see by comparing the height of the first and third peaks that the beat volume is decreasing at this point of the beat loudness cycle. Also shown is a sound file. The variation is difficult to hear in the sound file because the beats are so rapid. But if you listen very carefully you might just be able to catch it!