Is It Possible to Design an Unbreakable Cipher?

Is it possible to design an unbreakable cipher?

Do methods of encryption exist that guarantee privacy from even the most capable and highly-resourced of prying eyes? This question is especially relevant today, as individual privacy and national security increasingly find themselves at opposite ends of the arbitration table. Powerful nation-states with unparalleled mathematical know-how and prodigious amounts of computing power have been pounding away on modern encryption algorithms for decades, rattling the public’s confidence in the security of today’s most sophisticated ciphers. While this struggle might conjure images of a dismal arms race, there is, in fact, a theoretically secure encryption scheme—the ciphertext it generates is impossible to break even in principle. In 1949, mathematician Claude Shannon proved that a simple cipher, known since the turn of the century, if implemented properly would furnish the user with complete privacy. Shannon called this condition perfect secrecy.

Suppose you intercept the following ciphertext:

$\texttt{aixli tistp isjxl iyrmx ihwxe xiwmr wvhiv xsjsv qeqsv itivj igxyr msriw xefpm}$
$\texttt{wlnyw xmgim rwyvi hsqiw xmgxv eruym pmxct vszmh ijsvx ligsq qsrhi jirgi tvsqs}$
$\texttt{xixli kiriv epaip jevie rhwig yvixl ifpiw wmrkw sjpmf ivxcx ssyvw ipziw erhsy}$
$\texttt{vtswx ivmxc hssvh emrer hiwxe fpmwl xlmwg srwxm xyxms rjsvx liyrm xihwx exiws jeqiv mge}$

Like any good cryptanalyst worth their salt, you begin by examining the frequency with which the different ciphertext characters appear:

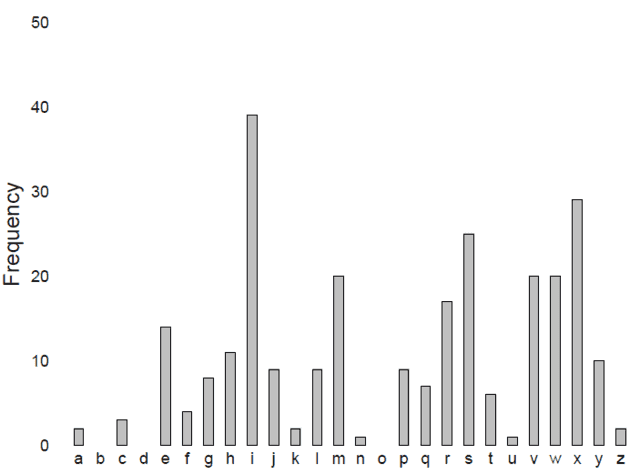
Fig 1. Letter frequencies appearing in the above ciphertext.

The resulting distribution is rough: certain letters like $\texttt{i}$, $\texttt{x}$, and $\texttt{s}$ appear notably more often than others. This is characteristic of spoken languages; for example, in English the five most common letters to appear in written correspondence are $\texttt{e}$, $\texttt{t}$, $\texttt{a}$, $\texttt{o}$, and $\texttt{i}$. You take a shot in the dark and suggest that your intercepted communication is a message written in English, and that the most common character of the ciphertext is a simple substitution of the most common character of the plaintext language, $\texttt{i} \leftrightarrow \texttt{e}$: to encrypt the letter $\texttt{e}$, it is shifted by four alphabetic characters to obtain the ciphertext letter $\texttt{i}$. Next, you surmise that the next most common ciphertext character, $\texttt{x}$, is likewise a simple substitution of some plaintext character, perhaps the next-most common, $\texttt{t}$. Interestingly, it too is the result of a shift of four. Here, however, your luck runs out: the third most-common ciphertext letter, $\texttt{s}$, is not a four-letter shift from the third most-common plaintext letter, $\texttt{a}$. But wait! It is four away from the fourth most-common plaintext letter, $\texttt{o}$! It is beginning to look quite likely that the ciphertext is a simple shift cipher: each character of the plaintext has been shifted by four letters to generate the ciphertext. The association is of course not perfect, though, since the intercepted ciphertext is but a meager sampling of the English language. Indeed, the smaller the sample, the less we expect character frequencies to match those appropriate to the English language at large.

Though the cryptanalyst’s hunch is correct—the cipher is indeed a simple substitution with a shift of four—it is only a hunch: the cryptanalyst cannot be certain of this conclusion. Instead, the cryptanalyst deals in probabilities and odds ratios, he studies the statistical distributions of ciphertext letters and makes imperfect inferences about the likelihoods of potential plaintext decryptions. Initially, before he gets his hands on any ciphertext, the cryptanalyst’s knowledge of the plaintext message, $M_i$, is minimal. Though the cryptanalyst might consider some messages more likely than others (based on the subject matter of the communication, the structure of the language, the capacity of the channel, and so forth) the a priori probability of any given message, $p(M_i)$, is exceedingly low. Now suppose that this message is encrypted as some ciphertext, $E_i$, and suppose that this ciphertext is intercepted by our cryptanalyst. The probability that the associated plaintext is $M_i$ is now $p(M_i|E_i)$. This is a conditional probability: given that the ciphertext has been obtained, how is the a priori probability of the message, $p(M_i)$, changed? In general, the acquisition of ciphertext provides at least some information regarding the underlying plaintext; in the case of the shift cipher, it provided enough information to confidently rule out all but one plaintext message¹, so that $p(M_i|E_i) \approx 1$.

This concept—that information about $M_i$ is potentially carried by $E_i$—is central to the design of secure ciphers. For the shift cipher, the frequency statistics of the plaintext are fully retained by the ciphertext: as more and more ciphertext is intercepted, the initially many possible plaintexts converge on an ever-smaller subset as the ciphertext letter frequencies approach those of the plaintext language. This is a general phenomenon: if the ciphertext exhibits any patterns of the plaintext language, gathering more of it will eventually tease them out, driving $p(M_i)$ towards unity. In general, then, we might conclude that $p(M_i)$ is a monotonically increasing function of $n$, the number of intercepted ciphertext characters. But is this always true? Is it inevitable that every cryptosystem exhibits this property, or is it possible to generate a ciphertext such that $P(M_i|E_i)$ never reaches unity, even as $n\rightarrow \infty$?

Consider the ciphertext with frequency distribution:

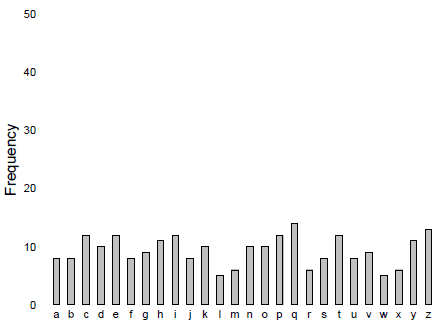
Fig 2. Frequency distribution of some seemingly random ciphertext.

In contrast to Figure 1 for the shift cipher, the frequencies of ciphertext characters are more or less uniformly distributed. It might be suggested that we need more ciphertext: maybe after several hundred more characters, some hint of structure will emerge. But what if Figure 2 summarizes the statistics after an arbitrary amount of ciphertext is collected? Claude Shannon’s realization was that if the ciphertext can be made truly random, then the uniformity of Figure 2 would persist indefinitely. With all features of the plaintext completely masked, the ciphertext is no help to the cryptanalyst, and $p(M_i|E_i) = p(M_i)$[itex]—the ciphertext discloses no information whatsoever about the plaintext. Shannon called this condition perfect secrecy because the cryptanalyst is maximally ignorant about $M_i$—any plaintext is perfectly fine candidate decryption. In what follows, we will sketch Shannon’s proof that the Vernam system, a substitution cipher with a random, non-repeating key, achieves perfect secrecy. As we’ll come to see, though, perfect secrecy is difficult to achieve in practice. So, what if instead of all plaintexts being suitable decipherments a cipher exists for which, say, one hundred plaintexts are suitable decipherments? Not perfect, but easier to implement and the cryptanalyst is still unable to single out unique decryption. Shannon called this condition ideal secrecy²—though the ciphertext might disclose some information about the $M_i$, it’s never enough, no matter how much of it the cryptanalyst collects, to reveal a unique decipherment. We’ll discuss this less rarefied class of ciphers too.

Shannon’s chief contribution to cryptology was to understand that the problem of decipherment was fundamentally one of information: specifically, information held by the cryptanalyst about the plaintext, $M_i$. Our first order of business will therefore be to relate the probabilities of messages to their information content and establish an information-theoretic statement of perfect secrecy.

The least probable is the most informative

Claude Shannon developed many of his ideas on cryptography in parallel with his work on the encoding and transmission of information across communication channels. Shannon recognized that the problem of separating the signal from interfering noise in the communication channel had deep connections with the problem of deciphering an encrypted message. His declassified work on cryptography, Communication Theory of Secrecy Systems [1] is built on many of the information-theoretic concepts developed in his foundational work A Mathematical Theory of Communication [2].

Imagine selecting a message from some language at random: $p_i$ is the probability that the $i^{th}$ character of the alphabet appears in this message. The quantity $-\log_2 p_i$ is the information content of the $i^{th}$ character³. The average information content per character of a language with an N-character alphabet is
\begin{equation}
\label{entropy}
H = -\sum_i^N p_i \log_2 p_i.
\end{equation}
Shannon recognized that the average information content per character gives a measure of the entropy, $H$, of the message space. Just as thermodynamic entropy applies to a volume of gas particles, Shannon’s entropy applies to collections of messages, like languages. The entropy is maximized when all letters appear in the language with equal frequency, $p_i = p$, so that each message is a random assortment of characters. Compare this “language” to English, where certain letters appear more frequently than others: for example, a word selected at random from English is more likely to possess an $\texttt{S}$ than a $\texttt{Z}$. We are therefore more certain that an $\texttt{S}$ will appear in a randomly selected English word than we are that an $\texttt{S}$ will appear in a language where all letters appear with equal frequency. Evidently, the higher the entropy of the message space, the more uniform the distribution of characters in the language, and so the lower our chances of correctly guessing the identity of a character (or message) drawn randomly from the language⁴. Simply stated, Shannon’s information entropy implies that the least probable events are the most informative.

Now, the entropy of the space of all possible messages associated with a given ciphertext can be written $H(M|E=E_i)$. From the definition above, Eq. (\ref{entropy}),
\begin{equation}
H(M|E=E_i) = -\sum_{j}p(M_j|E_i)\log p(M_j|E_i).
\end{equation}
This quantifies the average uncertainty that a cryptanalyst has regarding the possible plaintext decryptions of some interecepted ciphertext, $E_i$. We’d like to generalize this, though, so that it doesn’t refer to a specific ciphertext; this way, we can apply it to the entire cryptosystem—the complete space of messages and ciphertexts. So let’s average the conditional entropy $H(M|E=E_i)$ over all possible ciphertexts, $E_i$:
\begin{eqnarray}
H(M|E) &=& \sum_{i}p(E_i)H(M|E=E_i)\nonumber\\
\label{equiv}
&=&-\sum_{ij}p(E_i,M_j)\log p(M_j|E_i).
\end{eqnarray}
This is Shannon’s theoretical secrecy index, the equivocation⁵ of the message (we can also talk about the equivocation of the key, by summing over all possible keys, $K_k$, in Eq. (\ref{equiv}).) It formalizes the average degree of uncertainty, or ambiguity, regarding the plaintext associated with ciphertext generated by the cryptosystem. We can take Eq. (\ref{equiv}) a little further and write,
\begin{eqnarray}
H(M|E) &=& -\sum_{ij}p(E_i,M_j)\left[\log p(M_j) + \log \frac{p(E_i,M_j)}{p(E_i)p(M_j)}\right] \nonumber \\
\label{equiv2}
&=& H(M) – I(E;M),
\end{eqnarray}
where $I(E;M) = \sum_{i,j}p(E_i,M_j) \log p(E_i,M_j)/p(E_i)p(M_j)$ is the mutual information of plaintext and ciphertext, which is a measure of the amount of information obtained about the plaintext from the ciphertext. Eq. (\ref{equiv2}) succinctly summarizes the information theoretic view of decipherment: the uncertainty about the plaintext is reduced from our initial, broad uncertainty constrained only by knowledge of the language ($H(M)$) through information gleaned from the ciphertext ($I(E;M)$).

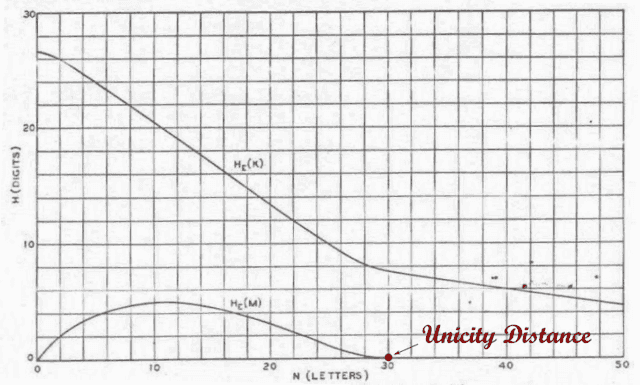
It’s useful to consider the equivocation as a function of $n$, the number of characters of ciphertext received by the cryptanalyst. If the ciphertext does not completely conceal plaintext characteristics, we expect the equivocation to be a decreasing function of $n$ (at least when $n$ isn’t too small) because as the ciphertext grows in length, any regularities and patterns become increasingly apparent and the cryptanalyst grows more and more certain of the range of possible plaintexts. If the ciphertext eventually reveals all of the characteristics of the plaintext language so that $I(E;M) = H(M)$, the equivocation drops to zero and only one plaintext decryption remains. Shannon called the number of ciphertext characters necessary for a unique decryption the unicity distance, $U$. In Figure 3, the message and key equivocations of the simple substitution cipher, in which each plaintext character is encrypted as a unique ciphertext character, is shown⁶:

Fig 3. Equivocation of English-language message, $H(M|E)$, and key, $H(K|E)$, as a function of the number of letters, $n$, in the intercepted ciphertext for a simple substitution cipher. The unicity distance, $U$, is marked. This figure is based on a recreation of Fig. 9 in [1].

It’s interesting that the two equivocations do not go to zero at the same number of intercepted letters: after all, once you’ve got the plaintext, haven’t you got the key? Not necessarily—if the intercepted ciphertext does not include at least one instance of each unique ciphertext character, then the cryptanalyst will have no way of knowing, even in principle, which plaintext characters they map to and so won’t recover the full key⁷. This is necessarily true of any English ciphertext with fewer than 26 characters, and as Figure 3 shows, only after $n=50$ characters on average does an English message include instances all 26 letters of the alphabet. Meanwhile, the message equivocation goes to zero at around $n=30$, since the cryptanalyst can recover the message without obtaining the full key. Just like our opening example with the shift cipher, once a few letters have been worked out, the structure of the language does the rest the constrain the range of possible messages.

At the opposite end of the spectrum from unique decipherment, $H(M|E) = 0$, perfect secrecy ensures that the ciphertext provides zero information about the plaintext, $I(E;M)=0$, and the the cryptanalyst is kept in a persistent state of maximal confusion, since $H(M|E) = H(M)$ is constant. Shannon cleanly demonstrated the requirements of the perfect cipher via a simple figure:

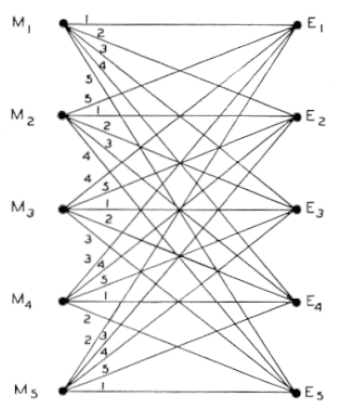
Fig 4. The perfect cipher has at least as many keys as messages. Figure from [1].

As long as the number of keys is at least as great as the number of messages, any given ciphertext has valid decryption to any plaintext. More generally, the entropy of the keyspace must be at least as great as that of the message space, $H(K) \geq H(M)$, so that whatever information is gained about possible plaintext decryptions is compensated for by the uncertainty over the possible keys.

The polyalphabetic substitution cipher known as the Vernam system achieves perfect secrecy by employing a random key as long as the message. The keyspace includes all meaningful English messages, like “$\texttt{Obviously, you’re not a golfer}$”, as well as all meaningless messages, like any of the effectively infinite number of garbled strings of letters, and so easily satisfies $H(K) > H(M)$. In modern implementations, the Vernam cipher combines a random binary keystream with decoded bits of plaintext using the logical bitwise operation exclusive or, or XOR, which works like: $1+0=0+1 = 1$ and $0+0 = 1+1 = 0$. The XOR operation transfers the randomness of the key to the plaintext to create a random ciphertext. Figure 5 illustrates this phenomenon, which occurs when the character sets and lengths of the key and plaintext are the same:
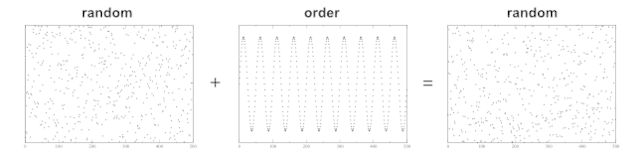Fig 5. 500 floating point numbers selected uniformly between the range [0,10] added $\mod 10$ to a $sin$ function on the same domain returns another uniform random distribution of floating points.  The analogy is random key + “ordered” plaintext yields a random ciphertext.

Because the ciphertext is random, it is statistically independent of the plaintext, so that $p(M_i|E_j)=p(M_i)$ and
\begin{equation}
I(E;M) \propto \log\frac{p(E_i,M_j)}{p(E_i)p(M_j)} = \log 1 = 0.
\end{equation}
Perfect secrecy is thereby assured. As an example, here is some ciphertext that nobody—not Alan Turing, not the NSA—nobody, can break:

$\texttt{asxle tiytp imjxl oyrmf ihwue xjwmr kvhiv bwjnv qeqsv itivj igxyr mkriw xefpm}$
$\texttt{wlnyw lmgim rwyvp hsqiw xmgev eruym pmect vdzmh qjsvp lqgsq gsrhi jhrgi tvsqs}$

The Vernam cipher has historically found widespread use, most noticeably during the Cold War: Soviet spies employed a version of the Vernam cipher using pre-deployed keys scrawled on note pads, earning this cryptosystem the moniker one-time pad. Likely due to the logistical difficulties of keeping unused, cryptographic-grade random keys around, the Soviets eventually re-used some their key material under the watchful eyes of U.S. and British signals intelligence, enabling some of their communications to be broken. Generating long, truly random keys is also hard: pseudo-random number generators, regardless of quality, churn out deterministic key streams that can in principle be broken. Natural sources of unbiased, independent bits, like noise from electronic circuits or radioactive decays, are ideal but generally not readily (or safely) available in sufficient supply to encrypt arbitrarily long messages, hence the modern proliferation of theoretically insecure but much more practical encryption methods like block ciphers.

Given the obstacles to achieving perfect secrecy in practice, let’s back away from the hard requirement that $H(M|E) = H(M)$ and examine instead the conditions under which ideal secrecy is attained. Here, though $H(M|E)$ is a decreasing function of $n$, the unicity distance is never reached: $U > n$. This is our new requirement.

$1 < H(M|E) < H(M)$: not perfect, but it should do

To understand the general characteristics of ciphers that exhibit ideal secrecy, we will compute the unicity distance of a model cipher called the random cipher [1,5]. The random cipher works as follows: given a ciphertext, $E_i$, and key, $K_k$, the ciphertext decrypts to some message, $M_j$, uniformly distributed across the space of all messages. Since $M_j$ is not determined uniquely by the pair $(E_i,K_k)$, the random cipher is really a whole ensemble of ciphers. This means we can apply statistics to the ensemble to model the unicity distance of a general cipher.

First, let’s examine the message space. We mentioned earlier that there are many more meaningless than meaningful messages in English⁸. Formally, if there are $N$ letters in a particular alphabet, then there are $N^{L} = 2^{R_0L}$ different $L$-letter sequences possible, where $R_0= \log_2 N$. The quantity $R_0$ is the entropy per letter of the “language” where each character has the same probability of occurrence, $p=1/N$. Entropy is maximized for such a language. Meanwhile, of all possible messages, a smaller number $2^{RL}$ will actually be meaningful in English, where $R$ is the entropy per letter, $H(M)/L$, of English. Because the letters in this restricted space of meaningful English sentences do not appear with equal probability, $R$ is smaller than $R_0$: with $N = 26$, we find $R_0 =4.7$ bits/letter, whereas $R$ is estimated to be around only $2.6$ bits/letter for 8-letter chunks of English, and $1.3$ bits/letter for more sizable chunks. $R$ is smaller than $R_0$ because the distribution of letters in English words is not random: per letter, there is less information on average in English.

A useful quantity is a redundancy of the language, $D = R_0 – R$: it is the maximum amount of information possible per character minus the actual amount of information so contained. For English, $D = 2.1$ for eight-letter words, meaning that around half of the letters in an eight-letter word of English word are superfluous, i.e. they are fixed by the structure of the language. For example, the letter $\texttt{q}$ is always followed by the letter $\texttt{u}$, and there must usually not be any more than three consonants in a row. If you’ve ever done one of those exercises where the vowels are removed from a typical English message and you find yourself still able to read it—that’s redundancy. It is relevant to data compression, which exploits regularities and patterns of language in order to maximize the information content per letter⁹. Anyway, it’s clear that the more redundant the language, the smaller the proportion of meaningful to meaningless messages. With these ideas in mind, consider the basic cryptosystem:

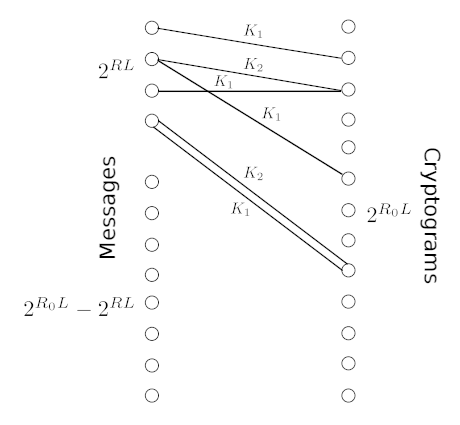
Fig 6. Schematic of a simple cryptosystem. Plaintext messages form the column on the left: the top group of $2^{RL}$ messages are meaningful; the bottom group of $2^{R_0L}-2^{RL}$ are meaningless. Two different keys connect the meaningful messages to the space of all possible cryptograms. The random cipher is an ensemble of such cryptosystems, each with a different mapping between messages and cryptograms. Figure adapted from Fig. 4 in [5].

Suppose a cryptanalyst has intercepted $n$ letters of an $L$-letter cryptogram. Figure 6 illustrates his situation vis-a-vis possible decryptions and keys. Of all possible plaintexts, we assume only meaningful messages, of which there are $2^{RL}$, are possible decryptions. Meanwhile, the ciphertext can take the form of any message, meaningful or not. There are more of these, $2^{R_0 L} > 2^{RL}$. Each plaintext message generally encrypts via different keys, of which there are $2^{H(K)}$, to different ciphertexts so that we have a one-to-many system. It is also possible that a given ciphertext decrypts via different keys into different meaningful messages. In other words, we might also have a many-to-one system—a situation known as a spurious message decipherment resulting in a nonzero message equivocation. For example, the cryptogram $\texttt{WNAJW}$ decrypts to $\texttt{RIVER}$ via a shift of 5 or $\texttt{ARENA}$ via a shift of 22. If this is the situation after the full cryptogram has been intercepted, $n=L$, then $U>L$ and the unicity distance lies beyond the size of the ciphertext, and unique meaningful decryption will be impossible.

While this is how we defined ideal secrecy, this isn’t the criterion we’ll use to explore it because determining the conditions under which spurious message decipherment occurs for the random cipher is hard. So rather than defining the unicity distance to be the number of intercepted letters needed to recover a unique message, we’ll identify it with the number of letters needed to recover a unique key, $U_K$. If $U_K > n$, then the cryptanalyst is unable to recover a unique key and is in a situation analogous spurious message decipherment, called spurious key decipherment. Note, though, that in general $U_K > U$ as we saw for the simple substitution cipher in Figure 3, and so the criteria we’ll determine for ideal secrecy will still be relevant, if a little on the conservative side. Therefore, in what follows, we’ll drop the subscript.

If the unicity distance can be made arbitrarily large so that $n<U$ generally, the cryptanalyst will always find himself in the situation of Figure 6. The best way to force a spurious key decipherment is to dump lots and lots of keys into the pot. In other words, the larger the entropy of the keyspace, $H(K)$, the more keys there are; this makes it harder to find the key, making spurious key decipherment more likely for a given amount, $n$, of intercepted ciphertext. And so $U$ grows with increasing $H(K)$. On the other hand, we assume that each of these keys yields a decipherment to any of the $2^{R_0L}$ possible messages chosen at random; only a number $2^{RL}$ of which are actually meaningful. So, the smaller the proportion of meaningful messages the less likely that a particular key will “land” you in the space of meaningful messages, where your decipherment is presumed to exist. A relatively small number of meaningful messages, then, makes it harder for there to be multiple keys yielding the same meaningful plaintext and hence lowers $U$.
To summarize, there are two factors that affect the unicity distance in opposite ways: the size of the key space (quantified in terms of $H(K)$), which is a property of the cryptosystem, acts to increase $U$, and redundancy (coming into play as the proportion of meaningful messages, $2^{RL}/2^{R_0L} = 2^{-LD}$), which is a property of the language, acts to decrease $U$. Note that these are essentially the two terms in Eq. (\ref{equiv2}) determining the equivocation: $I(E;M)$ is largely determined by $H(K)$, and $H(M)$ is summarized by $D$, the redundancy.

Putting these factors together, we can easily determine the expected number of spurious key decipherments, $\langle n_K \rangle$, under the assumption of our random cipher. The number of spurious keys should depend on the number of total keys and the relative number of meaningful messages. Specifically, assuming that there is one correct meaningful solution with key $K_j$, $\langle n_K \rangle = (2^{H(K)} -1)p$, where $p$ is the probability that any of the remaining $2^{H(K)} -1$ keys map to the same plaintext. What’s this probability? For the random cipher, it’s just $2^{RL}/2^{R_0L} = 2^{-LD}$—the chance that we land on a particular meaningful message! So we have then,
\begin{eqnarray}
\langle n_K \rangle = (2^{H(K)} -1)2^{-nD} &\approx& 2^{H(K)-nD},\\
&\approx& 2^{D\left(\frac{H(K)}{D}-n\right)}.
\end{eqnarray}
When the quantity $H(K)/D = n$, we have that $\langle n_K \rangle = 1$. This is the unicity distance,¹⁰
\begin{equation}
U = \frac{H(K)}{D}.
\end{equation}
For a ciphertext with $L$-letters, we can write
\begin{equation}
U = L\left[\frac{H(K)}{H_0 – H(M)}\right]
\end{equation}
where $H_0 = LR_0$ is the entropy of the full (meaningful and meaningless) message space. For perfect secrecy where the key is random, $H(K) = H_0$, $U > L$ as long as the entropy of the language $H(M) < H_0$. While no extant language has such a monstrous property, it’s possible to approach this limit using data compression techniques. Source coding, or ideal compression, reduces the redundancy of any message to zero, resulting in a randomized string. If we apply encryption to this compressed message, we can increase the unicity distance over-application of the same encryption to the original, uncompressed message. For this reason, many modern ciphers employ some sort of compression before encryption; however, they are not perfect because such ideal compression simply does not exist for spoken languages. For ideal secrecy, $H(K) \leq H_0$, and so we can’t draw any general conclusions without making assumptions about the entropy of the language, $H(M)$. For English, $H(M)/H_0 = R/R_0 = 1.3/4.7 = 0.27$ and so \begin{equation} U = 1.37 \times L \frac{H(K)}{H_0}, \end{equation} with the requirement that $H(K) > 0.73H_0$ in order to ensure that $U > L$. Interestingly, this amount of entropy per character is achieved with a random 11-character alphabet, since $0.73H_0 = \log 26^{0.73} \approx \log 11$—less than half the size of the randomized alphabet needed for perfect secrecy. Of course, the whole point of considering the more general class of ideal ciphers was to avoid the need for long, high-quality random keystreams. The lower entropy keyspace needed for ideal secrecy is actually provided by certain cryptographically secure pseudo-random number generators, meaning that only the initial seed data needs to be shared between sender and receiver. Ideal secrecy, it turns out, is practically achievable.

References and Footnotes

[1] Shannon, C. E., Communication Theory of Secrecy Systems. Bell System Technical Journal, 28 (1949).
[2] Shannon, C. E., A Mathematical Theory of Communication. Bell System Technical Journal, 27 (1948).
[3] Wyner, A. D., The wire-tap channel. Bell System Technical Journal, (1975).
[4] Blom, R. J., Bounds on Key Equivocation for Simple Substitution Ciphers. IEEE Transactions on Information Theory, IT-25 (1979).
[5] Hellman, M. E., An Extension of the Shannon Theory Approach to Cryptography. IEEE Transactions on Information Theory, IT-23 (1977).

¹If you’re not convinced, note that with only three plaintext characters cracked, the first three plaintext words are: $\texttt{_e t_e _eo__e}$. These are the first three words in a most famous political document. Can you figure it out? back
²Apparently, the words ideal and perfect aren’t synonyms in cryptology circles. back
³For example, “heads” in a coin toss conveys 1 bit of information, since $p_i = 1/2$. back
⁴Yes, Shannon’s conception of information content has the perhaps non-intuitive property that truly random messages are the most informative. This definition is evidently not concerned with the semantics or meaning, of the message. back
⁵This term I believe was first used by information theorist Aaron Wyner and defined by him “as a measure of the degree to which the wire-tapper is confused”; see [3]. For Shannon, this quantity arose out of the study of communication over discrete channels with noise: as a stream of bits is sent across a channel, the effect of noise is to randomly flip some of the bits. The task of the receiver is to reconstruct the original message from that received: the equivocation is an indication of the ambiguity of the received signal. See [2]. back
⁶This is a difficult quantity to study because the equivocation Eq. (\ref{equiv}) is challenging to calculate for most practical ciphers. For the simple substitution cipher, the key equivocation for a message of length $L$ is
\begin{equation}
\label{footn1}
H(K|E) = -\sum_{i=1}^{N!} \sum_{j} p(K_i)p(E_j)\log\left(\frac{\sum_{k}^{N!}p(E_j,K_k)}{p(K_i)}\right)
\end{equation}
where the sum over $j$ includes all cryptograms of length $L$. If ${\bf x} = (x_1,x_2,\cdots,x_N)$ is a vector containing the frequencies of the different characters in the plaintext, then the frequencies of the ciphertext characters are just permutations of this vector: $x_n = y_{t_i(n)}$, where the $t_i$ are the cipher transformations with key $K_i$, $M_k = t^{-1}_i E_j$. For the terms in Eq. (\ref{footn1}) we have $p(E_j) = p(t^{-1}_i E_j)=p(M_k)$. Yes, I know that’s a weird way to write it, but think about it. For simple substitution, the a priori chance that we obtain a certain ciphertext, $E_j$ is the same as having selected a certain message, $M_k$, at least as far as language statistics is concerned. Then, if $q_n$ is the probability of occurrence of the $n^{th}$ character, $p(E_j) = q_1^{x_1}q_2^{x_2}\cdots q_N^{x_N}$. Next, the prior probability of the key is just $p(K_i) = 1/N!$ because there are $N!$ different keys (the number of ways one can order the alphabet of $N$ letters) all equally probable. With these clarifications the equivocation can be written [4]
\begin{equation}
\label{foot2n}
\sum_{|x|=L}\frac{L!}{x_1!x_2!\cdots x_N!}\prod_{n=1}^{N}q_n^{x_n}\log \frac{\sum_{l=1}^{N!}\prod_{n=1}^N q_{n}^{y_{t_{i}(n)}}}{\prod_{n=1}^Nq_n^{x_n}}.
\end{equation}
Here we’ve replaced the notation $\sum_j$ in Eq. (\ref{footn1}) and the verbal caveat that the sum is to include all cryptograms of length $L$ with the sum $\sum_{|x| = L}$. The constraint $|x| = \sum_{n=1}^N x_i = L$ concerns the frequencies of the characters, but not their ordering. That’s what the term $L!/x_1!x_2!\cdots x_N!$ is for: it takes care of enumerating all of the unique words with the given frequencies ${\bf x}$, but we’ll have more to say about this in a moment. Evaluating Eq. (\ref{foot2n}) is hard: the probabilities $q_n$ depend on the length of word: it’s entirely possible that you’re generally more likely to find more $\texttt{p}$’s in ten-letter samples of English than four, and it is definitely true of uncommon letters like $\texttt{z}$. This makes it hard to evaluate Eq. (\ref{foot2n}) because these n-gram frequencies are hard to come by—someone needs to have worked them out. While these data exist for small groupings, and for large groupings the statistics of English at large apply, it’s the intermediate-length groupings that are difficult to handle. Eq. (\ref{foot2n}) is also a long sum, and that can be technically challenging! It’s an interesting sum, though, too. Of words of length $L$, we can have words of all the same letter (with $L!/L! =1$ combination), or 1 of one letter and $L-1$ of another (with $L!/1!(L-1)!$), or 2 of one letter and $L-2$ of another (with $L!/2!(L-2)!$ combinations), and so on. Or, we can have 1 of one letter, 1 of another, and $L-2$ of another (with $L!/1!1!(L-2)!$ combinations). While Eq. (\ref{foot2n}) tells us to perform the sum in this way, it’s up to us to enumerate all of these possibilities. The number of possibilities depends on $L$ in a special way: the terms in the denominators of the sum of the combination to $L$, and so the series sum is over all such possibilities. These are called the partition numbers of $L$, and the first few go like: 1, 2, 3, 5, 7, 11, 15, 22, 30, 42,… These numbers tell you how many distinct terms $L!/x_1!x_2!\cdots x_N!$ you have; and for each one there are $N \choose \ell$ copies for the $\ell$ letters represented (the number of nonzero $x_n$.) back
⁷This is a result of the fact that cryptanalyst has only a single ciphertext to work with—it’s the one he intercepted and was not of his choosing. This is called a known ciphertext attack as opposed to a chosen-ciphertext attack, in which the cryptanalyst can perform his own encryptions with the unknown key. back
⁸If this wasn’t true, cryptography wouldn’t work quite the same way. Consider a language in which every possible string of characters was a “meaningful” message. Then, even the ciphertext, which is supposed to be a random string of nonsense, would itself be a meaningful message in the language—as would every possible decryption! back
⁹James Joyce’s novel Finnegans Wake, with its improvised vocabulary and extravagant prose, is notably less compressible than other English novels. back
¹⁰We obtained this result using the key equivocation and the condition of spurious key decipherment. This is because the alternative approach—considering the message equivocation and associated spurious message decipherment—is much more difficult. That said, the average number of spurious message decipherments, $\langle n_M \rangle$, must satisfy $\langle n_M \rangle \leq \langle n_K \rangle$. This is because there are at least as many keys as meaningful messages, and generally, many more of the former (because the keys can be anything, meaningful or otherwise) and so the unicity distance derived above is applicable to the message equivocation as well. back