Beginners Guide to Precalculus, Calculus and Infinitesimals
Table of Contents
Introduction
I am convinced students learn Calculus far too late. In my view, there has never been a good reason for this.
In the US, they go through this sequence of Pre-Algebra, Algebra 1, Geometry, Algebra 2, Precalculus, Calculus 1, and Calculus 2. But is this required? Recently I came across two books that turned this on its head. Precalculus Made Difficult and Full Frontal Calculus:
https://www.bravernewmath.com/
Precalculus Made Difficult combines Algebra 1, Geometry, Algebra 2, and Precalculus into 220 pages. Typically I would start on Precalculus More Difficult, after what in the US system is called Pre-Algebra, which is generally done about year 7. It likely would take about a year to 18 months. Two years would also be reasonable. There is no hurry, as it is better to understand the concepts rather than rush through the material. Good students however could do it in a year. Then do Full Frontal Calculus. The Precalculus text is only 220 pages, and since it covers Algebra 1, Geometry, Algebra 2, and Precalculus is terse. It should be read slowly, ensuring each section is understood and completing all the exercises. If you run into any problems, post on Physics Forums, and me or someone else will be only too happy to help. The advantage of how I organised things in this article is the basics of Calculus are done before starting Full Frontal Calculus, allowing the study of a calculus-based Physics text in conjunction with the Calculus text. The Physics 2000 text I suggest in the conclusion also teaches basic Calculus. It aims to use Physics to help teach Calculus. Doing both together will provide an excellent introduction to Calculus. Students keen on math can obviously accelerate this. I personally taught myself Calculus at 13 – what was then year 9 in Queensland where I live. We started grade 1 at five instead of six.
When I learned calculus, the intuitive idea of infinitesimal was used. These are real numbers so small that, for all practical purposes (say 1/trillion to the power of a trillion) can be thrown away because they are negligible. That way, when defining the derivative, for example, you do not run into 0/0, but when required, you can throw infinitesimals away as being negligible.
This is fine for applied mathematicians, physicists, actuaries etc., who want it as a tool to use in their work. But mathematicians, while conceding it is OK to start that way, eventually will need to rectify using handwavey arguments and be logically sound. The usual way of doing it is using limits.
Instead, I will justify the idea of infinitesimals as legitimate. Not with full rigour; I leave that to my article What Are Numbers I will link to later, but enough to satisfy those interested in the fundamental ideas.
About 1960, mathematicians (notably Abraham Robinson) did something nifty. They created hyperreal numbers, which have real numbers plus actual infinitesimals.
Infinitesimals are numbers, x, with a very strange property. If X is any positive number -X<x<X or |x|<X. Normally zero is the only number with that property – but in the hyperreals, there are actual numbers not equal to zero whose absolute value is less than any positive number. We can legitimately neglect x if |x| < X for any positive real X. It also aligns with how many are likely to do calculus in practice. Even though I know calculus with limits, I hardly ever use it – instead, I use infinitesimals. After reading this, you can continue doing it, knowing it is logically sound.
As a beginner’s article, the reader likely has not seen precise definitions of integers, rationals, and real numbers. To correct this I have written another article on what What Are Numbers. It also goes deeper into the hyperrationals and hyperreals than is done here.
physicsforums.com/…ights/what-are-numbers
It is meant to be read after Full Frontal Calculus.
For now, read the first 6 Chapters of Precalculus More Difficult doing the exercises. Slowly does it. Make sure you understand all the concepts. This will take time. Then read the following on the hyperreals. Again take it slowly. It likely contains concepts not encountered before that will take a while to be acquainted with.
What Are Real Numbers
To build up to the hyperreals first we need a formal definition of what real numbers are. There are a number of such definitions, all equivalent, and my article What Are Numbers goes deeper into the issue.
The natural numbers are the counting numbers 0, 1, 2, …., n, …….. The integers extend this to include negative numbers eg …….,-n, ……… -3, -2, -1, 0, 1, 2 , 3 ……..n,…….. A rational number is simply a number that can be written as a/b where a and b are integers. Rational numbers can be extended to real numbers in a variety of ways. Here Dedekind Cuts will be used. Real numbers are an actual extension meaning rational numbers are also real numbers.
Conveniently real numbers, as well as all other numbers, can uniquely be represented by a point on the real number line.
Set Theory
Not much of set theory is needed. But its basics are useful in many areas of mathematics so it is worthwhile spending a bit of time learning the basics.
https://www.math.cmu.edu/~bkell/21110-2010s/sets.html
Remember this is just the basics. A deeper treatment will be given in the article What Are Numbers.
Dedekind Cuts
First note that between any two rational numbers y > x there is another rational number x + (y-x)/2.
A partition of the rational numbers divides all the rational numbers into two non empty sets A and B such that all the elements of B are greater than all the elements of A.
A Dedekind Cut is a partition of the rational numbers into two non-empty sets, A and B, such that A has no greatest rational.
If A and B is a partition of the rational numbers and A has a greatest element Q then simply removing Q from A and adding it to B will make it a Dedekind Cut. This is because between any two rational numbers there is another rational number. If Q is removed and A then has a greatest rational number, Q’, there is a rational between Q’ and Q that is an element of A. Contradiction. Hence A then has no greatest element so A and B are a Dedekind Cut
Real Numbers are defined as the set of all Dedekind Cuts.
Real Numbers are often thought of as points on the number line. In the language of Dedekind Cuts each point is called the cut-point of a Dedekind Cut and is the real number of the Dedekind Cut. A is all the rational numbers to the left of the cut-point; B is all the rational numbers to the right of the cut-point, including the cut-point itself if it is rational.
Two important results we need are if R’ is the cut-point of A’ and B’, and R is the cut-point of A and B; then R’ > all the elements of A implies A’ ⊇ A and R’ ≥ R. Also if R’ ≥ R then A’ ⊇ A. This is almost self-evident from cut points as points on the number line.
Hyperreals
Hyperreal Sequences
A sequence is an infinite list of numbers A1 A2 A3 ……… An. ………… This is sometimes written as An, meaning n is 1, 2, 3,……,n,……. Hyperreal sequences are sequences with an unusual definition of equality, less than, and greater than. Two hyperreal sequences A and B are equal if An = Bn except for a finite number of terms. Unless specifically referred to as sequences, equal sequences are considered a single object, what is called a Urelements. These are single objects used to represent a number of other objects defined to be the same. A < B is defined as An < Bn except for a finite number of terms. Similarly, A > B if An > Bn except for a finite number of terms. If R is a real number, the sequence R R R R…….. is the sequence of the number R. Of course, if A = R as a hyperrational sequence, then A is also a real number.
A + B is defined as An + Bn. A – B = An – Bn. A*B = An*Bn. A/B = An/Bn. In the definition of division, if Bn = 0 for a finite number of terms, the term An/Bn is set to zero. Of course, B ≠ 0.
A sequence X = Xn is finite if a positive number real number R exists |Xn| < R for all n. Suppose finite X ≥ zero then |X| is defined as X. If X < zero |X| = -X
Infinitesimals
Let X be any positive number. Let x be the sequence xn = 1/n. Then, an N can be found such that 1/n < X for any n > N. Hence, by the definition of less than in hyperrational sequences; x < X. Such hyperrational sequences are called infinitesimal. A sequence, x, is infinitesimal if |x| < X for any positive X. If x > 0, x is called a positive infinitesimal. If x < 0, x is called a negative infinitesimal. Normally zero is the only number with that property. Also, we have infinitesimals smaller than other infinitesimals, e.g. 1/n^2 < 1/n, except when n = 1.
Positive and Negative Unlimited Sequences
Sequences can also be positively unlimited ie larger than any number. Let A be the sequence An=n. If X is any number, there is an N such for all n > N, then An = n > X. Again; we have infinitely large numbers greater than other infinitely large numbers because except for n = 1, n^2 > n. Even 1 + n > n for all n.
Similarly, there are sequences such as A = An = -n less than any rational number ie negative unlimiteds.
Hyperreals Defined
Some sequences are pathological eg the sequence 1 0 1 0 1 0…… It is neither >, < or = 1. We want to define the hyperreals to avoid this issue.
Sequences that are positive or negatively unlimited are not pathological. Only finite sequences can be pathological.
To prevent this the hyperreals are defined as all the hyperreal sequences that are either =, >, or < any real number.
Functions Defined on the Hyperreals
If F(X) is a function where X is real number it can easily be extended to be defined on the hyperreals by F(X) = F(Xn) where X is a hyperreal. This property of the hyperreals is frequently needed in using hyperreals to do calculus. In particular if dx = xn is infinitesimal F(dx) = F(xn)
Unique Decomposition of Hyperreals
Let X be a finite hyperreal. Let A be the set of all the rationals < X and B the set of rationals ≥ X. A and B are a partition of the rational numbers. If A has a greatest rational then put it in B so A and B is a Dedekind Cut. A and B have R as its cut point. We claim R-X is infinitesimal.
By definition x is infinitesimal if |x| < X for any positive real X. If x = 0 then x is infinitesimal. If x is a positive infinitesimal then x < X for any positive real number X. If x is positive but not infinitesimal a positive real number s can be found s ≤ x. If x is a negative infinitesimal then x > X for any negative real number X. If x is negative but not an infinitesimal a negative real number s can be found s ≥ x.
Suppose X = R, R-X = 0. R-X is infinitesimal.
Suppose X < R. R – X is positive. If not infinitesimal there is a positive real S, S ≤ R-X. X ≤ R-S. Hence R-S > all elements of A. R-S ≥ R. S ≤ 0. But S is positive. Contradiction.
Suppose X > R. R – X is negative. If not infinitesimal, there is a negative real S, R-X ≤ S. R-S ≤ X. Since S is negative, R + S’ ≤ X, where S’ = -S is positive. R + S’ < X. If A’ and B’ is the Dedekind Cut with cut point R + S’ then since R+S’ < X, A’ ⊆ A. But R + S’ > R hence A’ ⊃ A. Contradiction. R – X is a negative infinitesimal.
Hence R-X is an infinitesimal. This implies X – R is also infinitesimal. Let r = X – R. X = R + r. Hence a finite hyperreal can be written as the sum of a real number and an infinitesimal. Is it unique? Suppose X = R1 + r1 = R2 + r2. R1 – R2 = r2 – r1. r2 – r1 is infinitesimal. Hence R1 – R2 is infinitesimal. But the only infinitesimal real number is zero. Hence R1 = R2 and r1 = r2. The decomposition is unique.
The finite hyperreals contain every real number. Let X = R + r where r is any infinitesimal, then X is a hyperrational. Therefore the finite hyperreals are all the numbers of the form where X = R + r, R any real and r any infinitesimal.
How It Is Applied
Applications are based on a simple observation. If x is infinitesimal then |x| < X where X is any positive real number. For real numbers only zero is infinitesimal. Since Calculus deals with real numbers, infinitesimals can legitimately be neglected ie taken as zero when desired. Since x can be neglected ie taken as zero, if c is any real number c*x is zero when x in taken as zero. This means c*x is also an infinitesimal. Note, as will be seen, if dy and dx are infinitesimal dy/dx may be finite. Similarly, again as will be seen, ∑ai where each ai is infinitesimal can be finite if there are an infinite number of ai.
Let’s say we want to find the instantaneous velocity of a particle at time t. Let Δt is a small difference in time, and x(t) the position at time t. If Δx = x(t+Δt) – x(t) is the change in distance during Δt then to good approximation Δx/Δt is the instantaneous velocity at time t, if Δt is small; with the approximation getting better as Δt is made smaller until it is exact if Δt = 0. If Δt = 0 then Δx/Δt = 0/0 which is undefined. Infinitesimals allow this problem to be circumvented. Let v(t) be the instantaneous velocity. Then v(t) = Δx/Δt + e(Δt) where e(Δt) is an error term that depends on Δt. If Δt is zero e(Δt) = e(0) = 0. Let Δt be the infinitesimal dt. This can be done because real functions, as shown previously, can be extended to the hyperreals. v(t) = dx/dt + e(dt). But dt can be neglected to give e(dt) = e(o) = 0. Hence v(t) = dx/dt. dx/dt is given the name of the derivative of x(t). dx/dt is also denoted by x'(t).
As another example, let S(x) be the slope of the tangent of f(x) at x. Let Δf = f(t+Δx) – f(x). If Δx small then to good approximation Δf/Δx is the slope of the tangent. S(x) = Δf/Δx to good approximation, with the approximation getting better as Δx is made smaller. As before if Δx = 0 then Δf/Δx = 0/0, which is undefined. Again infinitesimals resolve this. S(x) = Δx/Δt + e(Δx) where e(Δx) is an error term that depends on Δx. If Δx is zero e(Δx) = e(0) = 0. Let Δx be the infinitesimal dx. S(x) = df/dx + e(dx). But dx can be neglected. e(dx) = e(o) = 0. Hence S(x) = df/dx. df/dt = f'(x). The derivative of f(x), f'(x) = df/dx is the slope of the tangent of f(x) at x.
Some Derivative Formula
First a simple example. Let f(x) = x^2. df = (x +dx)^2 – x^2 = 2x*dx + dx^2 = dx*(2x + dx). Since dx is infinitesimal it can be neglected in 2x + dx. df = 2x*dx. df/dx = 2x.
We will derive some general formula for the derivatives of functions. d(f*g) = (f+df)*(g+dg) – f*g = f*dg + g*df + df*dg = dg*(f + g*df/dg + df). f and g*df/dg are real numbers, but df is infinitesimal so can be neglected. d(f*g) = dg*(f + g*df/dg + df ) = dg*(f + g*df/dg) = f*dg + g*df. (f*g)’ = d(f*g)/dx = f*(dg/dx) + g*(df/dx).
f(g(x))’ = df/dx = (df/dg)*(dg/dx) = f'(g(x))*g'(x).
As an application of the formula we will find the derivative of f(x) = x^n. A principle of reasoning called induction will be used. Suppose something is true for n =0. If it can be shown that when true for n it is true for n+1; it is true for all n. This is because it is true for n =0, hence true for n=1, n=2, n=3, and so on for any n. Suppose f'(x) = n*x^(n-1). Any number x^0 = 1. (x^o)’ = (1)’ = (1 – 1)/dx = 0/dx = 0. True for n=o. If true for n, (x^(n+1))’ = (x*(x^n))’ = x^n + x*(x^n)’ = x^n + x*n*(x^(n-1)) = x^n + n*(x^n) = (n+1)*x^n. Hence (x^n)’ = n*(x^(n-1)) is true for all n.
Lets find the derivative of f(x) = 1/x^n. Let g(x) = (x^n)/(x^n) = (x^n)*(x^-n) = (x/x)^n = 1. g'(x) = dg/dx = (x^n)*(x^-n)’ + n*(x^(n-1))*x^-n = 0. (x^n)*(x^-n)’ = -n*(x^(n-1))*(x^-n) = -n*x^-1. (x^-n)’ = -n*(x^-1/x^n) = -n*x^- (n + 1) = -n/x^(n+1).
This means the general rule is the same for any integer i. (x^i)’ = d(x^i)/dx = i*x^(i – 1) for i = ……. -3, -2, -1, 0, 1, 2, 3…….
Integration
Suppose f'(x) = df/dx = 0 for any x. Then if Δx is small (f(x+Δx) – f(x))/Δx = f'(x) to good approximation. f(x+Δx) = f(x) + f'(x)Δx = f(x) since f'(x) = 0. f(x) = f(0+n*(x/n)). If n is large then x/n is small and will be written as Δx. To good approximation f(0 + n*(Δx)) = f(0 + (n-1)*Δx + Δx) = f(0 + (n-1)*Δx) = f(0 + (n-2)*Δx) = f(0 + (n-3)*Δx)………. = f(0 + Δx) = f(0). To good approximation f(x) = f(0) with the approximation getting better as Δx is made smaller. f(x) = f(0) + e(Δx) where e is an error term. When Δx = 0 then there is no error ie e(0) = 0. We can’t simply let Δx = 0 because n would then be infinity and ∞ – 1 = ∞. The preceding derivation would not work. As usual let Δx = dx and e(dx) = e(0) = 0. f(x) = f(0) = C where C is a constant. If f'(x) = 0 then f(x) = C where C is a constant.
An antiderivative of f(x) is any function F(x), F'(x) = f(x). Suppose F1(x) and F2(x) are antiderivatives of f(x). (F1 – F2)’ = 0. F1 – F2 = C. F1 = F2 + C. Hence any antiderivative has the form F(x) + C where F(x) is an antiderivative. It is given a special name called the indefinite integral defined as ∫f(x)*dx. ∫f(x)*dx = F(x) + C. It actually is not a function, but a family of functions, such that if F(x) is a member of the family so is F(x) + C where C is any constant. The members of this family are all the antiderivatives of f(x).
The indefinite integral notation allows the easy derivation of a very important theorem called change of variables. ∫f*dy = ∫f*(dy/dx)*dx. It is used often in actually calculating integrals – or to be more exact antiderivatives.
Area
Without having any idea of what area is, from the definition of indefinite integral ∫1*dA = ∫dA = A + C where A is this thing called area. Doing a change of variable ∫dA = ∫(dA/dx)*dx. Let f(x) = dA/dx. ∫f(x)*dx = A(x) + C. We do not have a definition of A from this because of the unknown constant C. But note something interesting. A(b) – A(a) = A(b) + C – (A(a) + C). Now the arbitrary constant C has gone. This leads to the following unique definition of the area A between a and b. If A(x) is an antiderivative of a function f(x) the area between a and b, is defined as A(b) – A(a). It is given a special name – the definite integral denoted by ∫(a to b)f(x)dx = A(b) – A(a) where A(x) is an antiderivative of f(x). Note ∫(a to b)f(x)dx = A(b) – A(a) = -(A(a) – A(b)) = -∫(b to a)f(x)dx
A(x) could really be anything, and in many problems it is all sorts of things like volume or surface area. We will not pursue this further here as it is only a basic introduction to the ideas of calculus, but a textbook on calculus will. By introducing it this way it is easy to generalise.
Definite Integral as Infinitesimal Sums
The connection between area and the definite integral leads to another way to look at the definite integral.
First some notation. An interval [a,b] is all the real numbers between a and b including a and b.
Given a function f(x) defined on the interval [a,b], we divide the interval into n subintervals of equal width Δx and from each subinterval choose a point xi. The sum from i = 1 to n Σf(xi)Δx is called a Riemann sum of f(x) on [a,b]. If n is large, Δx is small and to good approximation Σf(xi)Δx = ∫(a to b)f(x)dx, the area under f(x) in the interval [a,b]. As Δx is made smaller the approximation becomes better; until if Δx is zero, it would be equal. But in that case f(x)Δx is zero. As usual introducing the error function e(Δx), ∫(a to b)f(x)dx = Σf(xi)Δx + e(Δx). Let Δx = dx, then dx can be neglected in e(dx) to give e(0) = 0. Also xi is in the interval [x,x+dx]. Again dx can be neglected to give the interval [x,x], hence xi = x. ∫(a to b)f(x)dx = Σf(x)dx. dx cant be neglected in Σf(x)dx as it is the sum of f(x)dx on an infinite number of infinitesimal intervals.
Intuitively ∫(a to b)f(x)dx can be viewed ∑f(x)dx ie the sum of all the infinitesimally small subintervals of width dx that [a,b] is divided into.
Exponential and Logarithmic Functions
If f(x) = x^i where i is an integer. df/dx = i*x^(i-1). ∫(x^i)dx = (1/(i+1))*x^(i+1) + C. Note the formula is not true if n = -1. So what is ∫(1/x)dx? Well because of the the C that appears in the integral this will be solved by defining a definite integral ln(x).
We define ln(x), x > 0, called the natural logarithm, as ln(x) = ∫(1 to x) (1/y) dy. Note ln(1) = 0 and ln'(x) = dln(x)/dx = 1/x. ln'(x*y) = y/x*y = 1/x (using f(g(x))’ = df/dx = (df/dg)*(dg/dx) = f'(g(x))*g'(x)). Hence since they have the same derivative ln(xy) = ln(x) + C. Let x = 1. ln(y) = C. ln(x*y) = ln(x) + ln(y). This is why the definite integral was from 1 to x. It leads to the simple relation ln(x*y) = ln(x) + ln(y).
An inverse of a function f(x), g(x), is a function such that f(g(x)) = x and g(f(x)) = x. Let e(x) be the inverse of ln(x). That ln(x) has an inverse is easily to see from its graph. Let a = e(x), b = e(y). ln(a) = x. ln(b) = y. e(x+y) = e(ln(a)+ln(b)) = e(ln(a*b)) = a*b = e(x)*e(y). Let e(1) = e, called Euler’s number. It is a very important number in math. e^n = e*e*…*e, n times. So e^n = e(n). So far e^n has only been defined for n a natural number. This allows us to define e^x for any x as e(x) and will from now on use e^x instead of e(x).
a^x is defined as e^(x*ln(a)). a^(x+y) = e^((x+y)*ln(a)) = e^(x*ln(a))*e^(y*ln(a)) = (a^x)*(a^y)
a^x = a^(0 + x) = a^0*a^x. Dividing by a^x we have a^0 = 1.
a^(x-x) = (a^x)*(a^-x) = 1. a^-x = 1/(a^x)
(a^x)^y = e^(y*ln(a^x)) = e^(y*ln(e^(x*ln(a)) = e^(y*x*ln(a)) = a^(x*y)
a = a^(x/x) = (a^(1 /x))^x or (x√)a = a^(1/x).
From this you should be able to derive all the exponent rules given in the Precalculus text, only this time for any real numbers. For example x^a/x^b = (x^a)*(1/x^b) = (x^a)*(x^-b) = x^(a-b),
The logarithm of x to base a will be written as loga(x) and is the inverse of a^x, if it exists. Suppose a^x has an inverse then a^(loga(x)) = x. e^(loga(x)*ln(a)) = x. ln(x) = loga(x)*ln(a). The logarithm to base a is defined as loga(x) = ln(x)/ln(a). We want to show that ln(x)/ln(a) is the inverse of a^x. a^(ln(x)/ln(a)) = e^(ln(a)*ln(x)/ln(a)) = e^ln(x) = x. loga(a^x) = ln(a^x)/ln(a) = ln(e^(x*ln(a))/ln(a) = x*ln(a)/ln(a) = x. Hence the inverse of a^x, loga(x) exists and is ln(x)/ln(a)
loga(x) has the usual properties of logarithms. loga(xy) = ln(xy)/ln(a) = (ln(x) + ln(y))/ln(a) = loga(x) + loga(y).
Now we look at some calculus. log(e^x) = x. (1/e^x)*(e^x)’ = 1. e^x = (e^x)’. The derivative of e^x is the same function. Very interesting.
Lets find the derivative of x^a when a is not just an integer but any real number. (x^a)’ = (e^(a*ln(x))’ = e^(a*ln(x))*(a*ln(x)’ = e^(a*ln(x))*a/x = a*(x^a)/x = a*x^(a-1). Hence the general formula is the same as when a = n.
Read the rest of Precalculus More Difficult. The above should have made Chapter 7 easier to understand as we have used Calculus. This is just one example of its power.
Complex Numbers
One omission of Precalculus Made Harder is complex numbers. It is covered in Full Frontal Calculus, but it is such a beautiful example of the power of Calculus, often not explained well, I cant resist introducing it here.
Consider the real line as the x-axis in the plane. We know -1 is an operator that rotates a real number by 180%. I generalise that to F(x) being an operator that rotates a real number by an angle x in the plane. Of course rotation is additive, F(x+y) = F(x)F(y). We define F(90%) as i and note i^2 = -1 ie a rotation by 180%. i = √(-1) is called the ‘imaginary’ number i. But here, it is not imaginary at all – but is a simple process of rotation. This leads to what are called complex numbers.
It is a very interesting area not just mathematically, but historically and its applications:
https://www.veritasium.com/videos/2021/11/1/this-problem-broke-math-and-led-to-quantum-physics
A point in the plane (x,y) = (x,0) + (0,y). Since (x,0) and (y,0) lie on the x axis, which can be taken as the real number line, then (x,0) = x and (0,y) = iy, where the real number y has been rotated by the imaginary number i to give (0,y). (x,y) = (x,0) + (0,y) = x + i*y and the y axis becomes the complex line. Of course, in this form points in the plane become complex numbers. This view of complex numbers is expanded on using Trigonometry. Imaginary numbers simply extends rotation of a real number from 180% to include 90%. In fact we will see that F(x) is itself a very interesting complex number.
Euler’s Relation
Let F(x) as the rotation operator defined previously
F'(x) = (F(x + dx) – F(x))/dx = ((F(dx) – 1)/dx)*F(x) = i’*dx where the operator i’ = (F(dx) – 1)/dx. F(Δ(x)) is approximately 1 + i*Δ(x), as can be seen by rotating a line through a small angle Δ(x). F(Δ(x)) is approximately 1 + i*Δx with the approximation getting better as Δ(x) gets smaller and is exact if Δ(x) = 0. But that would mean no rotation, so as usual we do the error term argument. F(Δ(x)) = 1 + i*Δx + e(Δx) and let Δ(x) = dx. e(dx) = 0. F(dx) = 1 + i*dx. I think the pattern is now clear. The error term step can be skipped and simply say F(dx) = 1 + i*dx. i’ = (1 + i*dx – 1)/dx = i. Hence F'(x) = i*F(x).
dF/dx = i*F. dF/F = i*dx Integrating both sides ∫1/F*dF = ∫i*dx. ln(F(x)) = ix + C. e^(ln(F(x))) = e^(ix + C) = C’*e^ic where C’ = e^C. F(x) = C’*e^ix. Let x = 0. C’ = 1. F(x) = e^ix.
Now things move quickly. Rotating 1 on the real axis by the angle x gives in the complex plane gives F(x) = cos(x) + i*sine(x) = e^(i*x) which of is one of the most famous relations in all of mathematics. It is called Euler’s relation.
Trigonometry From Euler’s Relation
Ok we have Euler’s Relation. This will make trigonometry easier than Precalculus Made Hard.
First is the derivative of sine and cos. (e^ix) = (cos(x) + i*sine(x))’ = i*e^(ix) = i*(cos(x) + i*sine(x)) = i*cos(x) – sine(x).
cos(x)’ = -sine(x). sine(x)’ = cos(x)
sine(x+y) + i*cos(x+y) = (cos(x) + i*sine(x))(cos(y) + i*sine(y)) = cos(x)*cos(y) + i*cos(x)*sine(y) + i*sine(x)cos(y) – sine(x)*sine(y) = cos(x)*cos(y) – sine(x)*sine(y) + i*(cos(x)*sine(y) + sine(x)cos(y)).
Equating the real and imaginary parts gives:
cos(x+y) = cos(x)*cos(y) – sine(x)*sine(y).
sine(x+y) = cos(x)*sine(y) + sine(x)cos(y).
Precalculus Made Hard has proofs of Pythagorus Theorem. Now for one that only involves Euler’s Relation
e^ix = cos(x) + i*sine(x). and e^-ix = cos(x) – i*sine(x). Adding and subtracting.
cos(x) = (e^ix + e^-ix)/2 and sine(x) = (e^ix – e^-ix)/2i.
Do some algebra and we find cos(x)^2 + sine(x)^2 = 1.
Let a + ib be any complex number. Its length r is the hypotenuse of the right angled triangle with sides a and b. But a + ib is the length r rotated by an angle x. a + ib = r*(cos(x) + i*sine(x)). a/r + ib/r = cos(x) + i*sine(x). Since cos(x)^2 + sine(x)^2 = 1 we have (a/r)^2 + (b/r)^2 = 1. a^2 + b^2 = r^2 which is Pythagorus Theorem.
Complex numbers are covered in Full Frontal Calculus but if you would like a head start:
https://www2.clarku.edu/faculty/djoyce/complex/
Conclusion
Now is the time to read Full Frontal Calculus. The brief introduction to calculus here will make studying the book easier.
It uses the infinitesimal approach but does not develop the theory of infinitesimals it is based on as done here. But the reader will know enough to fill in the gaps so to speak.
At the same time a calculus based physics textbook can be studied. The following not only teaches physics but Calculus as well:
Doing both together will reinforce the concepts from each book.
Then the legendary Feynman Lectures on Physics. Note: Do not be tempted to study it before a calculus based physics book – that is NOT recommended. When Feynman gave the course the students gradually left and were replaced by upper level and graduate students. The lectures explain the meaning behind the basic concepts that should already be known. They should be known first, or like happened to the original students, it may not work well. Just about every physics text recommends the lectures as supplemental reading, for those that love physics like Feynman did, but no course uses it as its primary text .
Then you can delve even deeper by doing Lenny Susskind’s Theoretical Minimum:
The Theoretical Minimum (5 book series)
All this from just knowing the basics of calculus along with doing the exercises.
I have have given an overview of the hyperreals. This is expanded on in my insights article on What Are Numbers.
For further advice on studying math after Full Frontal Calculus:
A Guide to Self Study Calculus | Physics Forums
Personally after Full Frontal Calculus I would study Boaz:
Mathematical Methods in the Physical Science’s
Then Hubbard:
Vector Calculus, Linear Algebra, and Differential Forms: A Unified Approach
Good luck on your journey. I hope my introduction has given enough detail for anyone with the curiosity about the beautiful, interesting and powerful subject of Calculus to start the journey of discovery. As Silvanus Thompson said in his classic Calculus Made Easy, ‘What one fool can do, another can.’
My favourite interest is exactly how can we view the world so what science tells us is intuitive.








This is just a small section of your article that I took a close look at. I haven't looked closely at the other parts. Here are some comments about your work as well as ways that I would write this differently.
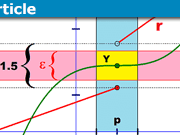
Instead of X I would use ##\epsilon##, which is typically used in many mathematics textbooks to denote a "reasonably small" but positive real number.
Instead of "Let x be the sequence xn = 1/n." I would define an identifier S like so, using set notation: Let S be the sequence ##\{x_n : x_n = \frac 1 n, n \in \mathbb N \}##
Your inequality "x < X" leaves a lot unstated and hurts my head to look at. Namely that a sequence x of numbers (which I'm calling S) is less than a single positive real number X (which I'm calling ##\epsilon##. I think you addressed this in another Insights article, but it would be good to also include it here. My version of this would be that ##S < \epsilon## means that all but a finite number of elements in S are less than ##\epsilon##.
You wrote: "A sequence, x, is infinitesimal if |x| < X"
You haven't defined the absolute value/norm of a sequence, or if you did, I missed it. If I have a sequence ##S = \{1/2, 1/3, 1/4, \dots, 1/n, \dots \}## and ##\epsilon = 0.01##, what's the value of |S| here? And how can I determine whether ##|S| < \epsilon##?
Last, I'm not sure that you need to talk about hyperrationals as opposed to hyperreals. All the number in my sequence are rationals, sure enough, but they are also reals. If I search for "hyperrational" on the internet, I don't get a lot of results.
Valid point. It has been a long time since I used LaTex. It will take a while, but I will fix it.
Thanks
Bill