Super p-Brane Theory Emerging from Super Homotopy Theory

 

A notorious open problem:

What is the non-perturbative theory formerly known as Strings?

We still have no fundamental formulation of “M-theory” – the hypothetical theory of which 11-dimensional supergravity and the five string theories are all special limiting cases. Work on formulating the fundamental principles underlying M-theory has noticeably waned. […]. If history is a good guide, then we should expect that anything as profound and far-reaching as a fully satisfactory formulation of M-theory is surely going to lead to new and novel mathematics. Regrettably, it is a problem the community seems to have put aside – temporarily.

But, ultimately, Physical Mathematics must return to this grand issue.

(G. Moore, Physical Mathematics and the Future, talk at Strings 2014)

At the conference StringMath 2017 I am invited to parallel-speak about recent results with D. Fiorenza, J. Huerta, and H. Sati on this question:

• Super p-Brane Theory emerges from Super Homotopy Theory
  based on arXiv:1611.06536 and arXiv:1702.01774
  (talk slides, lecture notes)

Here is an invitation.

---

What are even the principles of the theory?

Two principles worth considering:

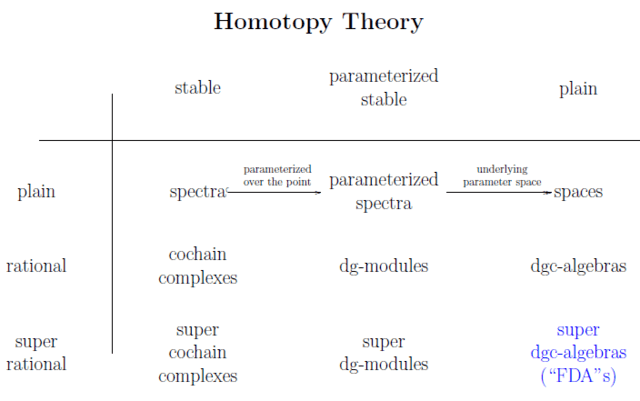
1. The gauge principle: No two different things are ever equal, instead they may be related by a gauge equivalence. Consequently, no two different gauge transformations are ever equal, instead, they may be related by a gauge-of-gauge equivalence. And so on. Mathematically this is the principle of homotopy theory. Gauge equivalence is homotopy, and gauge-of-gauge equivalence is higher homotopy. For example, a BRST complex with $n$th order ghosts-of-ghost fields is mathematically an infinitesimal homotopy $n$-type. This is also called a rational homotopy type due to the fact that the BRST-type dgc-algebra that represents it is over a field of characteristic zero.
2. The Pauli exclusion principle: No two fermions are in the same state. Mathematically this is the principle of super-geometry: fermionic elements of a super-commutative algebra anti-commute with each other.

The unification of these two principles is super-homotopy theory.

Its infinitesimal/rational approximation is familiar: The cofibrant super dgc-algebras (Koszul dual to super $L_\infty$-algebras) that represent it are the “FDA”s from supergravity theory (this coincidence is part of the convoluted history of the concept of $L_\infty$-algebras):

---

Homotopy theory

In mathematics, homotopy theory is famous for the rich structure that it conjures from minimal input. For example, the homotopy groups already of the simplest cell complexes that exist, the $n$-spheres, exhibit endless patterns, order, and chaos, the real Music of the Spheres. Generations of mathematicians crank these out with heavy machinery such as the Adams spectral sequence.

These graphics, taken from Hatcher,  shows the 2-primary components of the first few dozen stable homotopy groups of spheres computed this way.

Each point here has a story associated with it. For instance, the three points directly over the numbers 1, 3 and 7, correspond to the complex, the quaternionic, and the octonionic Hopf fibrations. The complex Hopf fibration is an $S^3  = SU(2)$-principal bundle over the 4-sphere whose total space is the 7-sphere

$$ \array{ S^3 &\longrightarrow& S^7 \\ && \downarrow \\ && S^4 }$$

This will re-appear below, emerging from the super-point, via the Fierz identity for the GS-WZW term of the M5-brane

A filtration knows as chromatic homotopy theory proves that the most advanced tools available in homotopy theory, the topological modular forms that host the super-partition function of the heterotic string, are but the second stage of this filtration. Endless wonders lie beyond, waiting to be discovered.

---

The inner structure of homotopy types.

The microscope of homotopy theory is the Postnikov-Whitehead tower.
Applied to any homotopy type it reveals an infinite Russian doll’s inner structure.

For example the Whitehead tower of the stable orthogonal group reveals an infinite tower of groups whose first stages are named after NS-sector phenomena of string theory: The
spin group, the string group, the fivebrane group, the nine brand group.

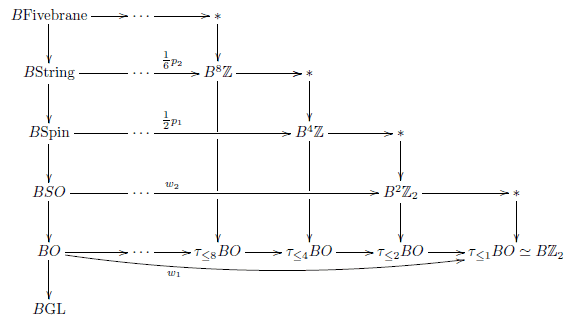
Graphics from dcct: horizontally runs the Postnikov tower, vertically the Whitehead tower of the classifying space $BO$ of the stable orthogonal group.

The Whitehead tower has a simple construction principle: Given a homotopy type (such as $B O$), find its maximal 1-cocycle (in the above picture, the total bottom horizontal map to $B \mathbb{Z}_2$) and form the extension that it classifies, its homotopy fiber (in the above situation: the first vertical map on the left over $B O$). On that extension find the maximal 2-cocycle (in the abovee picture the map to $B^2 \mathbb{Z}$), and extend again (the next vertical map). And so forth.

In the example of the Whitehead tower of the orthogonal group, the 3-cocycle is the third integral Stiefel-Whitney class, obstructing Spin structure, then next is the 4-cocycle which is the Green-Schwarz anomaly, obstructing String structure, then next is the 8-cocycle which is the Green-Schwarz anomaly of dual heterotic string theory obstructing NS-Fivebrane structure, and so on.

(graphics from dcct)

We are talking about pure homotopy theory, and yet stringy terminology keeps appearing. As another example, the string orientation of tmf is an intrinsic homotopy theoretic thing, discovered and studied by mathematicians who know no string theory. And yet it computes the partition function of the heterotic string. What is going on?

---

In order to see more clearly, we should proceed more systematically.
We should start at the beginning.

At the beginning in super-homotopy theory there is the super-point,

$$\mathbb{R}^{0 \vert 1}$$

the atom of superspace. We may apply Whitehead’s microscope to it and discover which structures hide inside.

A movie zooming into the superpoint in super homotopy theory is shown in the talk slides. The emergence from the super-point  of super-spacetimes and of super p-branes was also the topic in an earlier article in this series: Emergence from the Superpoint. The brane bouquet that emerges is the following:

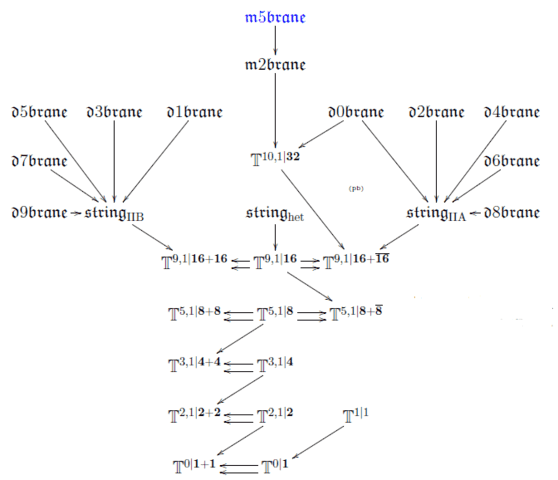
There is more. As one zooms into the superpoint in super homotopy theory, one dicovers ( arXiv:1308.5264, arXiv:1606.03206, arXiv:1611.06536 . arXiv:1702.01774):

• First of all space-time itself,
• then superstrings,
• the D-branes,
• RR-fields in twisted K-theory,
• D0-brane condensation growing an 11th dimension,
• M-branes, M-brane charge in cohomotopy,
• double dimensional reduction,
• T-duality, Buscher rules for RR-fields
• doubled spacetime,
• the F-theory fibration,
• S-duality.
• …

The talk slides show this in action, for detailed exposition see the lecture notes.

In conclusion, a fair bit of the expected structure of M-theory emerges, rationally, in super-homotopy theory from the super-point. More should be there, but this is how far we got.

Perhaps we need to understand the nature of time itself better. […] One natural way to approach that question would be to understand in what sense time itself is an emergent concept, and one natural way to make sense of such a notion is to understand how pseudo-Riemannian geometry can emerge from more fundamental and abstract notions such as categories of branes.

(G. Moore, Physical Mathematics and the Future, talk at Strings 2014)

I will explain some further aspects of this below. The impact however is that we obtain an evident conjecture about the full theory:

The full structure of M-theory
emerges analogously from an extension sequence
in full super-homotopy theory.

This remains to be worked out.

But here is one fact:

In full super homotopy theory,
the super-point $\mathbb{R}^{0| 1}$ itself
emerges from $\emptyset$
by a sequence of dualites and their sublations:

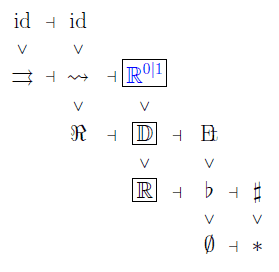
This is beyond the scope of the present article, but you may find details in

• Modern Physics formalized in Modal Homotopy Type Theory
  to appear in
  S. Centrone, D. Kant and D. Sarikaya (eds.)
  What are suitable criteria for a Foundation of Mathematics?
  Springer

---

M-Branes in the Music of the Spheres

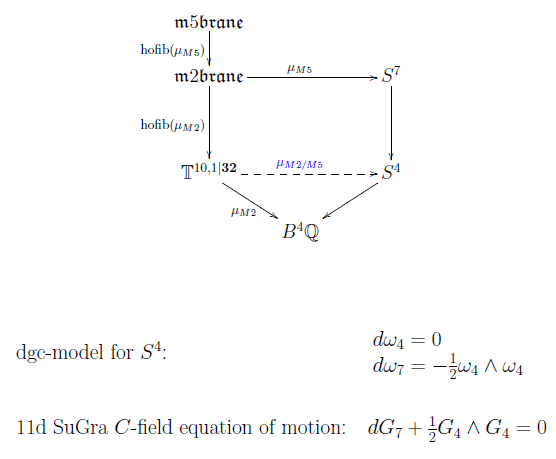
One result of this process is that the M-brane charge is, rationally, in degree 4 cohomotopy, namely is represented by a field with values in the 4-sphere $S^4$, rationally (arXiv:1506.07557).

To see what this means, observe that the Sullivan model for $S^4$ is the following dgc-algebra (“FDA”)

$$ d \omega_4 = 0 $$  $$   d \omega_7 = – \tfrac{1}{2} \omega_4 \wedge \omega_4 $$

Hence a super-field on 11d superspacetime with coefficients in $S^4$ is, rationally,

1. a super 4-form $G_4$
2. a super 7-form $G_7$

such that

$$d G_4 = 0$$
$$d G_7  + \tfrac{1}{2} G_4 \wedge G_4 = 0$$

These are the equations of motion of the C-field in 11d-supergravity.

The super 4-form here is the Green-Schwarz-WZW term of the M2-brane

$$ G_4 = \tfrac{i}{2} \overline{\psi} \wedge \Gamma_{a b} \psi  \wedge e^a  \wedge e^b $$

while the super 7-form here is the GS-WZW term of the M5-brane

$$G_7 = \tfrac{1}{5!} \overline{\psi} \wedge \Gamma_{a_1 \cdots a_6} \psi \wedge e^{a_1} \wedge \cdots \wedge e^{a_5} $$.

That these fermion bilinears indeed satisfy the dgc-model for the 4-sphere is due to a remarkable Fierz identity that is originally due to D’Auria-Fré 82. An unexpected chord in the music of the spheres.

More it true: the way the $C_3$-field for the M2-brane twists the $C_6$ field for the M5-brane is governed by the quaternionic Hopf fibration:

---

Another cherished principle is Duality. Mathematically, duality is adjunction and in homotopy theory this is derived adjunction.

Write $B S^1$ for the homotopy type that classifies circle extensions.

Theorem:

There is an adjunction, hence a duality, between

• ($\mathrm{Ext}$) letting a super-spacetime grow an extra compact dimension in the form of a circle bundle
• ($\mathrm{Cyc}$) forming the cyclic loop space of a super-spacetime.

In fact this is just a special case of a more general duality that applies to higher torus bundles and  generally for fibrations of group-like $A_\infty$-spaces. For details see the lecture notes here.

That these are adjoint means in particular that for every super-spacetime $X$ carrying a cocycle for a circle extension, there is a canonical map

$$X \overset{\eta}{\longrightarrow} \mathrm{Cyc} \mathrm{Ext} (X)$$

from $X$ to the cyclic loop space of its extension. This means that if

$$ \phi : \mathrm{Ext}(X) \longrightarrow A $$

is a super-field with coefficents in $A$, then its dual (its adjunct) is

$$ X  \overset{\eta}{\longrightarrow} \mathrm{Cyc} \mathrm{Ext} (X) \overset{\mathrm{Cyc}(\phi)}{\longrightarrow}  \mathrm{Cyc}(A), $$

hence is a field on the lower dimensional spacetime, but now with coefficients being the cyclification of the original coefficients.

---

We may apply this to compute the double dimensional reduction of the 4-sphere valued M2/M5 cocycle

$$\mathbb{T}^{10,1\vert \mathbf{32}} \longrightarrow S^4$$

to a cocycle on the type IIA super-spacetime, with coefficients in the cyclic loop space of the 4-sphere:

$$ \mathbb{T}^{9,1\vert \mathbf{16}+ \overline{\mathbf{16}}} \longrightarrow \mathcal{L}S^4/S^1.$$

Remarkably, the cofibrant dgc-model (“FDA”) for this cyclic loop space exhibits the twisted cohomology famous from D-brane charge (this is worked out here):

$d h_3 = 0$
$d \omega_2 = 0$
$d \omega_4 = h_3 \wedge \omega_2$
$d \omega_6 = h_3 \wedge \omega_2$
$d h_7 = \omega_2 \wedge \omega_6 – \tfrac{1}{2} \omega_4 \wedge \omega_4$

Therefore the double dimensional reduction of the above M2/M5-brane cocycle produces a system of super-differential forms that satsfies

$d H_3 = 0$

$d F_2 = 0$
$d F_4 = H_3 \wedge F_2$
$d F_6 = H_3 \wedge F_2$
$d H_7 = F_2 \wedge F_6 – \tfrac{1}{2} F_4 \wedge F_4$

This is the Bianchi identities for the fields that couple to the double
dimensional reduction of the M2 brane and the M5-brane: the F1-string, the D0-brane, the D2-brane, the D4, brane and the NS5-brane. And indeed, working out the above formula for the adjunct, one finds the GS-WZW terms for these branes (arXiv:1606.03206).

The remaining type IIA D-branes arise similarly from the music of the spheres: The 4-sphere itself is an $S^1$-extension, namely of the orbifold $S^4/S^1$, where $S^4$ is identified with the unit sphere in the direct sum of the real numbers with the quaternions. The sub-orbifolds $S^4/\mathbb{Z}_n$ are familiar as the near horizon geometry of M5-branes at A-type singularities (Medeiros & Figueroa-O’Farrill 10, section 8.3).

Asking for gauge enhancement is now to ask for a lift of the above cyclification through the adjunction unit of the 4-sphere, which is $S^4/S^1 \longrightarrow \mathrm{Cyc}(S^4)$. This does not exist globally, but it exists, in Goodwillie-linearization, where the fibration $S^4/S^1 \longrightarrow S^3$ is replaced by its fiberwise stabilization $\Sigma^\infty_{S^3}(S^4/S^1)$. This was computed in Roig-Saralegi 00 and remarkably, it contains a full copy of the twisted cohomology complex

$d h_3 = 0$

$d \omega_{2p+2} = h_3 \wedge \omega_{2p}$

(see here)

---

Repeating this double dimensional reduction via cyclification of brane cocycles pass further down from 10d t0 9d. One discovers a system of homotopy fibers that exhibits super T-duality in its mathematical incarnation known as topological T-duality, rationally. Namely as the following diagram shows

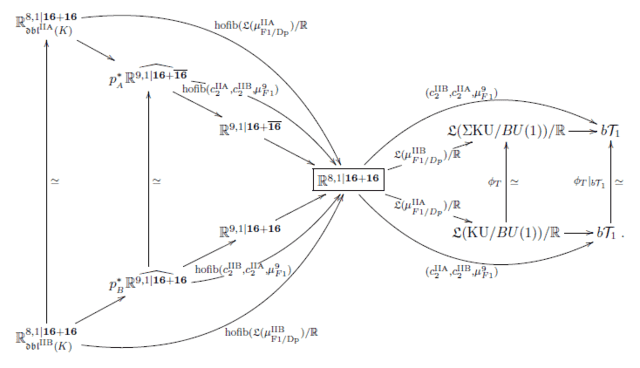
one finds that the unified cocycles $\mu^{\mathrm{IIA}}_{F1/Dp}$ and $\mu^{\mathrm{IIB}}_{F1/p}$ for the string and D-branes on d=10 type IIA and type IIB superspacetimes, respectively,  become equivalent as cocycles after double dimensional reduction, this is the triangle on the right of the above diagram. In components this equivalence turns out to be the Buscher rules for RR-fields under T-duality.

By functoriality of homotopy fibers, this implies that the homotopy fibers of these cocycles becomes equivalent, and this is reflected by the corresponding triangle on the left of the above diagram. Computation shows that this homotopy fiber in each case is the corresponding doubled super-spacetime carrying the pullback of the B-field gerbe, hence their equivalence is now T-duality made manifest as a symmetry of the doubled IIB superspacetime. (For more details you need to see arXiv:1611.06536. )

In other words it means that the following structures appear from the superpoint in super-homotopy theory:

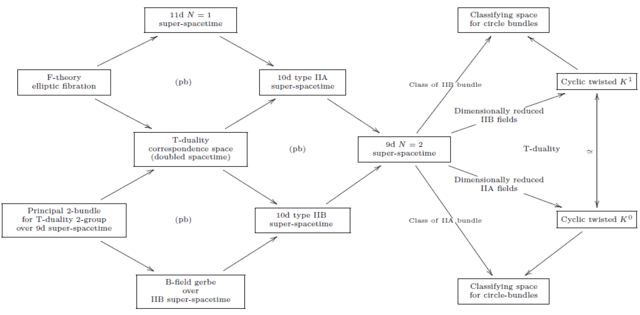
This here is not the place to discuss further details. These are in  arXiv:1611.06536 and in the lecture notes.