What Is the Bell Spaceship Paradox, and How Is It Resolved?
Bell describes two spaceships that start out at rest relative to each other, with an elastic string between them, one end attached to each ship, which is initially just long enough to span the distance between the ships without being stretched.
![]()
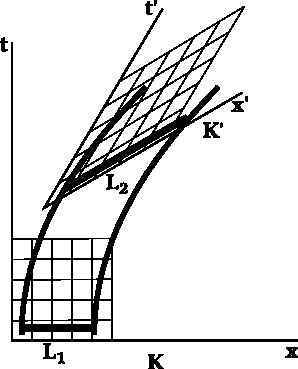
The ships’ clocks are synchronized in their common initial rest frame K. At some time t by their clocks, both of them turn on their rockets and start accelerating in the positive x direction, with the same constant proper acceleration (meaning that the crew of each ship feels the same constant acceleration). What happens to the string?
The correct answer is that, as the ships accelerate, the string is stretched more and more until it breaks. The “paradox” arises from the following (erroneous) line of argument: since both ships start accelerating at the same time, and they both have the same acceleration, the distance between them should remain constant, so how can the string be stretched and break?
Of course, in relativity, whenever you see an argument using the terms “time” and “distance,” you know you need to be careful since time and distance are frame-dependent. To resolve the “paradox,” we look at the distance between the ships, as seen from the instantaneous rest frame K’ of either ship. If you do this at different points along either ship’s worldline, you will see that the distance gradually increases, e.g., L2>L1 for the two lengths shown in the figure, as measured on the respective graph-paper grids. These lengths are measured parallel to the spacelike axes of frames K and K’, so that they are distances between events that are simultaneous as measured in these frames. Since the string remains attached to both ships, increasing the distance between the ships in either ship’s instantaneous rest frame means the string has to stretch (and eventually it will stretch enough to break).
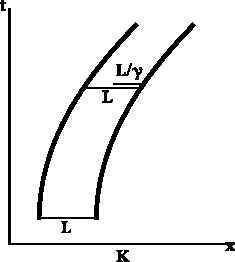
Some treatments of the paradox attribute the breaking of the string to “length contraction,” and you may be wondering how that comes into play since the discussion so far has not mentioned it. In the article by John Bell in which he originally introduced the paradox, he gave an alternate line of reasoning to get the correct answer. The ships and the string are originally set up at rest relative to one another, with the string unstressed. As the ships accelerate, the string moves faster and faster relative to frame K, so its “natural” (i.e., unstressed) length, as measured in K, gets shorter and shorter due to length contraction. But its actual length as measured in K does stay the same, so the string will be increasingly stretched until it breaks. (It may be helpful to consider the case where an additional, identical string is attached only to the front spaceship. As the ships accelerate, they retain their original length, as measured in their rest frame, and are therefore too short to span the increased distance between the ships. The shorter line marked L/γ in the diagram below can be thought of as representing this second string.)
Bell’s argument is valid. However, note that what is “contracted” is not the actual length of the string in the original rest frame, but its “unstressed” length in that frame. The actual length of the string in the original rest frame stays the same, so the use of the term “length contraction” in this connection is a little unusual: normally that term is used to refer to a length that is measured in some frame. That’s why, if you ask whether the string in the Bell spaceship paradox breaks due to “length contraction,” the answer is not a straightforward “yes.”
References
J.S. Bell, “How to teach special relativity,” in Speakable and unspeakable in quantum mechanics, 1988, Cambridge University Press
http://en.wikipedia.org/wiki/Bell_spaceship_paradox
http://www.lightandmatter.com/sr/ (source for diagrams, somewhat modified for this FAQ)
The following forum members contributed to this FAQ:
PeterDonis
WannabeNewton
PAllen
ZapperZ
jtbell
bcrowell
tiny-tim
PhD in physics. I teach physics at Fullerton College, a community college in Southern California. I enjoy writing, playing viola, brewing beer, climbing and mountaineering.






Just for fun: you can compare how the Bell spaceship paradox is resolved in the both SR and Lorentz theory. Just consider that after initial acceleration the spaceships turn their engines a 180 degrees and start their engines running again. Will that bring them back into the original position? http://Www.theoryrelativity.com
Excuse the noob observation here – but isn’t this to do with the problem of observation and measuring everything in terms of ‘light’ and observed effects?
What happens in actuality to the string? Surely it stays at the same length in reality. If the ships accelerate to light spped, then decelerate to rest, would the string physically be broken or would it still be intact?
There is not much of a paradox here. As the pair of ships approach the speed of light the string won’t break unless you mechanically try to make it the same length as it would have been at rest. Everything contracts uniformly including the string and the space between the ships and the ruler you measure everything with. If there really was a problem with the string breaking then spaceships themselves would have to be infinitely short or they would break apart at near light speed.
Imagine a ship with a nuclear thruster that would have to be far from the human pilots. It might be very long with a giant nuclear engine in the rear connected by a tubular frame to the human occupied module in front. The entire assembly including the connecting tube would be subject to the Lorentz contraction as it approached the speed of light. Nothing unusual would happen from the perspective of the crew. The ship and everything in it would look perfectly normal to the crew and the ship would not be subject to any unusual forces other than the engine thrust. Of course running into micro meteorites or something larger would not be fun but that has little to do with the so called paradox.
“The ships’ clocks are synchronized in their common initial rest frame K. ”
Intertial.
Shurely.
-dlj.
Now it would be great, if you could point me to a source where this coordinate independent definition of #21 is explained in detail. I must admit I still do not even understand the meaning of the various symbols used in this posting. Is this in terms of Rindler coordinates, i.e., an accelerated reference frame comoving with either B or C (and if so, is there a difference between these two choices and what measures the distance deciding whether the rope breaks or not)?I wrote this up as an example at the end of section 9.5 in my SR book: http://www.lightandmatter.com/sr/ . The coordinates used there are Minkowski coordinates.
Thread closed.
Hi @JD96,1) there is no issue with the length of the string. The entire universe is accelerating and shrinking, breaking the string.The paradox description causes some confusions in understanding. Since two spaceships are starting at exactly the same point of time and always are moving with the same acceleration, they can be considered as a single unit. BUT, there is a space between them (this is the condition of string breaking). Now, from the string frame of reference, two ships and string are standing still, but it's the entire universe who is accelerating and shrinking. So, from the elastic string point of view, the space between ships is shrinking, causing it to break. Take it easy, don't make things more difficult than they are. Read about "length contraction" http://newt.phys.unsw.edu.au/einsteinlight/jw/module4_time_dilation.htm
Who called this phenomena "paradox"?? Why we make things even more complex than they are? This topic is a great example of pseudoscientific confusion, means opposite to the science. Let me sort it out. If two ships start moving at exactly same point in time, with exactly same acceleration, than whats the difference if it were a single unit? The conditions are the same if it were a single ship. According to the predictions and experiments which were done since the middle of the past century, length of the body, which is moving at high speed (near the speed of light) is NOT CONSTANT. This is well known phenomena, called "contraction of length". From the ships point of view or from the string frame of reference – they are standing still, it's the entire universe who is accelerating and shrinking, causing elastic string to break, This is the point ))))) so funny, nothing mysterious or paradoxical.
This is getting very off-topic.I've moved the "modeling of measurements" posts to a separate thread.
This is getting very off-topic.
Thanks, PeterDonis — that was all very helpful!
I don't understand this comment. Both cases involve accelerated motion, considered in a fixed inertial frame (the frame in which all the objects are at rest at time ##t = 0##). The difference is that in case a, the proper acceleration varies along the congruence (i.e., as a function of the constant ##c## labeling the worldlines–here ##c## is in fact the reciprocal of the acceleration, in geometric units, or more precisely its square) in just the right way to keep the expansion scalar zero for the congruence. In case b, the proper acceleration is constant (here ##c## just translates the same hyperbola, with proper acceleration 1, in the ##x## direction of the inertial frame), which leads to a positive expansion scalar.Yep, you're right, I messed up the interpretation. I think a better motivation for considering this congruence is that its world-lines have constant proper acceleration a, and each such world-line has a constant position in Rindler coordinates. The interpretation is that although rigid bodies are not in general possible in relativity, it is possible to apply a set of external forces to a straight rod so that it accelerates along its own length without any stress. This is a unique property of Rindler coordinates.
Then, for case a, we have
$$
gamma = frac{1}{sqrt{1 – u^2}} = frac{x}{sqrt{x^2 – t^2}}
$$
$$
u gamma = frac{t}{x} frac{1}{sqrt{1 – u^2}} = frac{t}{sqrt{x^2 – t^2}}
$$Actually, I just noticed that there's an even simpler way to show that ##Theta = 0##. From the equation for the hyperbolas in case a, the denominator in both these expressions above is just the constant ##c## (or actually its square root as bcrowell wrote it)! So trivially, ##gamma## is only a function of ##x## and ##u gamma## is only a function of ##t##, and ##Theta## vanishes identically. In fact we have ##gamma = a x## and ##u gamma = a t##, where ##a## is the proper acceleration of the worldline (and varies with ##c##, but not with ##x## or ##t## for a given worldline with fixed ##c##).
This makes sense because in case a we're considering inertial motion, but in different coordinatesI don't understand this comment. Both cases involve accelerated motion, considered in a fixed inertial frame (the frame in which all the objects are at rest at time ##t = 0##). The difference is that in case a, the proper acceleration varies along the congruence (i.e., as a function of the constant ##c## labeling the worldlines–here ##c## is in fact the reciprocal of the acceleration, in geometric units, or more precisely its square) in just the right way to keep the expansion scalar zero for the congruence. In case b, the proper acceleration is constant (here ##c## just translates the same hyperbola, with proper acceleration 1, in the ##x## direction of the inertial frame), which leads to a positive expansion scalar.
I believe case a is just the case where we have a bunch of objects at rest relative to one another in their own rest frame, but we switch to Rindler coordinates, while b is a bunch of world-lines, all with proper acceleration 1, i.e., the situation in the Bell spaceship paradox.Yes, I agree.
In case a we have ##u=t/x##, while in case b we have ##u=t/sqrt{1+t^2}##. (I could have messed this up.)This looks right to me.
Then ##Theta=partialgamma/partial t+partial(ugamma)/partial t##,I think you mean ##Theta = partial gamma / partial t + partial ( u gamma ) / partial x##, correct? That's what your code says. :wink:
When I run it as shown, for case b, I get that ##Theta=gamma u^2/t##, which is positive for ##t>0##. When I uncomment the first line and comment out the second, I get that ##Theta=0##.Yes, this looks correct, although the case b expression can be simplified, as I'll show below. But the algebra isn't actually that involved.
For case b, the key is to notice that ##partial ( u gamma ) / partial x = 0##, because ##u##, and therefore ##gamma##, is a function of ##t## only. So we reduce the computation to ##Theta = partial gamma / partial t##, and we have
$$
gamma = frac{1}{sqrt{1 – u^2}} = sqrt{1 + t^2} = frac{t}{u}
$$
and therefore
$$
Theta = frac{d gamma}{dt} = frac{t}{sqrt{1 + t^2}} = u = frac{t}{u} frac{u^2}{t} = gamma frac{u^2}{t}
$$
which agrees with what you got from Maxima, but ##Theta = u## is easier to remember. :wink:
Then, for case a, we have
$$
gamma = frac{1}{sqrt{1 – u^2}} = frac{x}{sqrt{x^2 – t^2}}
$$
$$
u gamma = frac{t}{x} frac{1}{sqrt{1 – u^2}} = frac{t}{sqrt{x^2 – t^2}}
$$
and therefore
$$
Theta = frac{partial gamma}{partial t} + frac{partial ( u gamma )}{partial x} = – frac{x t}{left( x^2 – t^2 right)^{3/2}} + frac{x t}{left( x^2 – t^2 right)^{3/2}} = 0
$$
This calculation is nice because it shows the symmetry between ##gamma## and ##u gamma##, which is what makes ##Theta## vanish.
The simplest mathematics that expresses, in a way independent of frames and coordinates, your statement in ordinary language that "the proper distance between the ships increases with time" is the expansion scalar of the congruence of worldlines describing the ships and the string. This expansion scalar is an invariant, and it is positive; that is the invariant way of saying that the proper distance increases.I had never gotten around to doing this calculation explicitly, so I thought I'd give it a shot. I considered two congruences: (a) world-lines defined by ##x^2-t^2=c##, and (b) ##(x+c)^2=1+t^2##. In both cases ##c## is a parameter that tells us which world-line we're talking about. The part that I think I'm most likely to have messed up is defining these and interpreting them properly. I believe case a is just the case where we have a bunch of objects at rest relative to one another in their own rest frame, but we switch to Rindler coordinates, while b is a bunch of world-lines, all with proper acceleration 1, i.e., the situation in the Bell spaceship paradox.
For the expansion scalar, we have ##Theta=partial_a v^a##. Restrict to 1+1 dimensions, and let ##u=dx/dt##. Then ##Theta=partialgamma/partial t+partial(ugamma)/partial t##, and Born-rigidity is equivalent to vanishing ##Theta## (we can't have shear in 1+1 dimensions). In case a we have ##u=t/x##, while in case b we have ##u=t/sqrt{1+t^2}##. (I could have messed this up.) The algebra gets a little messy, so I did it using Maxima. Here's my code:
/* u:t/x; */
u:t/sqrt(1+t^2);
gamma:1/sqrt(1-u^2);
theta:diff(gamma,t)+diff(u*gamma,x);
is(equal(theta,0));
is(equal(theta,gamma*u^2/t));
When I run it as shown, for case b, I get that ##Theta=gamma u^2/t##, which is positive for ##t>0##. When I uncomment the first line and comment out the second, I get that ##Theta=0##. This makes sense because in case a we're considering inertial motion, but in different coordinates, and the expansion scalar is coordinate-independent.
Does this seem right?
the question is, why does the proper distance get larger with time. We have a setup that would not obviously change that proper distance, so it requires an answer as to why it had that effect. And here is where we choose a reference frame and/or coordinate system, depending on how you parse those concepts.You can answer the question without having to pick a reference frame or coordinate system at all. See below.
There is no other way to express physics adequately than mathematics.Yes, but often there will be more than one piece of mathematics that expresses a given piece of physics, and which mathematics you pick matters. See below.
I don't know, how else one can explain this apparent paradox.The simplest mathematics that expresses, in a way independent of frames and coordinates, your statement in ordinary language that "the proper distance between the ships increases with time" is the expansion scalar of the congruence of worldlines describing the ships and the string. This expansion scalar is an invariant, and it is positive; that is the invariant way of saying that the proper distance increases.
There is no other way to express physics adequately than mathematics. I don't know, how else one can explain this apparent paradox. Isn't it also clear from the Minkowski diagram that the signal starting the acceleration of the two space ships is different from the point of view of the instantaneous rest frames. The signal to start accelerating is simultaneous only in A's rest frame. If you have an idea to explain this better, let me know.
I don't know what you mean by your last sentences. The physical laws are uniquely and precisely formulated in both Newtonian and Minkowksi space time, using the adequate mathematics. That's it. Further, with science we don't answer "why questions", because by definition science is an as precise as possible description of nature based on objectively observable and quantifiable phenomena, no more nor less. It does not answer, "why" the physical laws we discover from precise measurements and theory building are as they are.
As you can read in my new (not ready) FAQ article, the reason is in fact very simple: The proper distance between the space ships which is the required length of the rope to connect the space shipd gets larger with time.Sure, but the question is, why does the proper distance get larger with time. We have a setup that would not obviously change that proper distance, so it requires an answer as to why it had that effect. And here is where we choose a reference frame and/or coordinate system, depending on how you parse those concepts. We do that to generate a language to answer why questions, like why does proper distance increase when two rockets take off simultaneously.
In A's reference frame the distance between the ships is constant, but this is the length-contracted proper distance. I think the explanation in Bell's book is pretty complicated compared to this simple observation. I hope my FAQ explains it simpler (as also does the here discussed Insight article):
http://fias.uni-frankfurt.de/~hees/pf-faq/srt.pdfYour approach is to show how it emerges from the mathematics, and then to provide a kind of physical explanation using notions like length contraction and the relativity of simultaneity. Those are what I mean by language that stems from choosing a coordinatization, in this case the standard Einstein simultaneity convention applied in the original frame. So what I'm saying is, when people try to get insight into a "why" question, they want a more physical feeling answer than just the solution to the mathematics, and that's where a choice of coordinates comes in– but that's also where the uniqueness of the answer is lost. So that's what I think it is the lesson of the Bell paradox: in relativity, we often sacrifice uniqueness to obtain a physical answer to a why question. I'm not taking anything away from a well though-out and elegant mathematical treatment, which is often helpful at seeing more intuitive kinds of physical explanations, I'm just pointing out how curious and important it is to recognize that physical explanations are generally not unique. We're used to them depending on the physical laws chosen, but in relativity we also see nonuniqueness within a single set of physical laws, because of the inherent association with coordinatization.
What I think this "paradox" is best at bringing out is that there really does not exist a "correct" language to say "why" the string breaks. The physics prediction is only that the string breaks– the why question simply does not have a unique answer.As you can read in my new (not ready) FAQ article, the reason is in fact very simple: The proper distance between the space ships which is the required length of the rope to connect the space shipd gets larger with time. So the rope must break. In A's reference frame the distance between the ships is constant, but this is the length-contracted proper distance. I think the explanation in Bell's book is pretty complicated compared to this simple observation. I hope my FAQ explains it simpler (as also does the here discussed Insight article):
http://fias.uni-frankfurt.de/~hees/pf-faq/srt.pdf
But the whole point of the EP is that you don't have to pick a particular piece of the worldlines of the two ships; in the analogy being made, the two ships are both at rest in the same gravitational field, so it doesn't matter where on their worldlines you pick your "local" region, since the field is static.Thanks again for clearing that up to me, too. Then I will keep in mind that although one in principle could use the EP to explain why the weak field approximation for gravitational time dilation and the ratio of the proper times in Bell's setup have the same form, one should use the scenario involving different proper accelerations when the primary goal is to understand gravitational time dilation.
not even when considering that it is an approximation where the velocity of primed K is assumed to be low compared to the speed of light, so that the distance between them approximately stays the same in primed K?Not really. Look at it this way: suppose we have one rear ship R and two front ships. Front ship A has the same proper acceleration as R; front ship B has a lower proper acceleration, lower by just enough so that the two will remain the same distance apart indefinitely in their momentary rest frame.
The EP argument for gravitational time dilation depends on the fact that the ships are accelerating: a light ray released, for example, by the rear ship will be redshifted when it reaches the front ship, because the front ship has started moving away from the light in the time it took the light to cover the distance between the two. But if we have two front ships with different accelerations, then they will be moving away from the light from the rear ship at different speeds, and will therefore see different redshifts.
Now, you could, I suppose, restrict yourself to such a small distance between the ships that the difference in their speeds away from the rear ship, in the time it takes light to travel between the two, is negligible. But then you're restricting yourself also to a small patch of spacetime around the "origin" event–the event where the rear ship first starts to accelerate. Once you've left that small patch of spacetime, the difference in acceleration between front ship A and front ship B will mean that the distance from the rear ship to front ship A is no longer small enough for your approximation to hold. But the whole point of the EP is that you don't have to pick a particular piece of the worldlines of the two ships; in the analogy being made, the two ships are both at rest in the same gravitational field, so it doesn't matter where on their worldlines you pick your "local" region, since the field is static. Front ship B works for this analogy, but front ship A does not; in other words, front ship A can't be viewed as at rest in the same static gravitational field as the rear ship.
Nobody can directly measure the unstressed rest length of the string if the string is under stress. The string being under stress is an invariant; it doesn't depend on your choice of frame, and all observers agree on it.I should have noticed the bad wording "observing unstressed length" in my previous post, but your answer nonetheless adresses what I had in mind, namely that unprimed K's explanation of the breaking of the string should involve the unstressed length being shortened by the lorentz factor.
You also need knowledge about how solid objects are put together, physically.Ah I see, so one would need to consider the electromagnetic interactions between the atoms and molecules of the string to really understand why the unstressed length of the object stays the same. I agree that this is probably going over my head and I will follow your advice and leave that to microphysics :-)
Then what you are saying is not correct, at least not as an application of the equivalence principle. To apply the EP, the ships would have to be at rest relative to each other while they are accelerating, since the analogy is to objects at rest in a gravitational field at slightly different altitudes.Mhh, not even when considering that it is an approximation where the velocity of primed K is assumed to be low compared to the speed of light, so that the distance between them approximately stays the same in primed K?
No. A "gravitational field" in this sense does not automatically imply spacetime curvature, because you are only sampling it locally.That makes it clear to me, thanks.
when you write the length of the string stays constant in unprimed K, it's because each end of the string is always attached to one of the spaceships and since the problem is set up, so that the distance between the spaceship remains the same in K, the "actual" length of the string will also stay constant until it breaks.Yes.
when an observer in unprimed K wants to account for the breaking of the string using length contraction he should observe the unstressed length of the string be shortened by the lorentz factor, which I would argue means primed K should measure the unstressed rest length.Nobody can directly measure the unstressed rest length of the string if the string is under stress. The string being under stress is an invariant; it doesn't depend on your choice of frame, and all observers agree on it.
When the observer in K says that the "unstressed length" of the string is shortened by the Lorentz factor, that's really a sloppy way of saying that if the string were not under stress, its measured length in K would be shortened by the Lorentz factor. But this is a counterfactual, not an actual measurement.
how do we know the unstressed rest length stays constantBecause this is how the physics of strings works. More precisely, it's how the physics of solid objects in general works; their rest length when not under stress is an invariant property of the object.
It's true that this fact about objects is not something you can deduce purely from the postulates of SR. You also need knowledge about how solid objects are put together, physically. But for purposes of this scenario, you don't need to know any gory details of the microphysics of solid objects; you just need to know that that microphysics justifies the claim I made in the previous paragraph.
with the ratio of the proper time I mean the following (now I am referring to the minkowski diagram in the insight post)…Then what you are saying is not correct, at least not as an application of the equivalence principle. To apply the EP, the ships would have to be at rest relative to each other while they are accelerating, since the analogy is to objects at rest in a gravitational field at slightly different altitudes.
an accelerating observer will justify him being at rest, despite feeling proper acceleration, via a gravitational fieldYes, this is true, as long as you interpret "gravitational field" correctly. See below.
so that from an accelerating observer's perspective there's automatically spacetime curvature and other general relativistic effects involvedNo. A "gravitational field" in this sense does not automatically imply spacetime curvature, because you are only sampling it locally. Locally, if you are feeling a 1 g acceleration, you can't tell whether it's because you're in a rocket in flat spacetime whose engine is producing 1 g of thrust ("gravitational field" present, but no spacetime curvature), or standing at rest on the surface of the Earth (gravitational field and spacetime curvature). But if you are allowed to make observations over a larger region of space and time, you will be able to tell the difference.
A recent post I made looking at clock synchronisation and simultaneity (also looking at one way speed of light) seemed to suggest that it is impossible to prove simultaneity without assuming the speed of light is isotropic as there is no physical test that can be made to prove it.The fact that the two ships fire their engines simultaneously, in the frame in which they are originally at rest, is not something that has to be proven for this scenario; it is assumed as a condition of the scenario. The definition of simultaneity used is Einstein clock synchronization.
if that logic applies, then it must equally apply to this paradox in so much as it must be impossible to say which ship moves first.Of course it's possible; you just need to specify what frame you are using. Specifying a frame means assuming a particular simultaneity convention; it doesn't require proving one (which is, of course, impossible since simultaneity is not absolute). Of course that also involves assuming that the speed of light is isotropic and that the one-way speed of light equals the two-way speed. All of these are assumptions, which are justified by the fact that the theory that makes them, special relativity, correctly predicts the results of experiments.
In the frame that the two spaceships end up in, assuming they accelerate rapidly and reach a final cruising speed, what you will see is two spaceships moving toward you, back end first, some distance L apart. Then the engine at the front fires, breaking the rope, and then the engine at the back fires.Ah, I see. Yes, you're right, you can always make either one of a pair of spacelike separated events occur first by an appropriate choice of frame.
The only point I see here that still might require clarification is that you say "the engine at the front fires, breaking the rope, and then the engine at the back fires". I don't think you can say definitely that, in the frame in which the two spaceships are finally at rest, the rope breaks before the engine of the rear ship fires. In fact, it seems unlikely to me that that would be the case. It will, however, always be the case that the front ship's engine fires first in this frame.
(Btw, the Bell spaceship scenario does not require assuming that there is such a frame; the ships could keep accelerating indefinitely, or they could stop in such a way that they are not at rest in the same inertial frame.)
It doesn't; it increases. The length of the string stays the same in the original rest frame, K (no prime), but the string is not at rest in that frame once the ships start accelerating.I am realizing I forgot to distinguish between unstressed and "actual" length as done in the insight post and probably that is where my confusion comes from. So when you write the length of the string stays constant in unprimed K, it's because each end of the string is always attached to one of the spaceships and since the problem is set up, so that the distance between the spaceship remains the same in K, the "actual" length of the string will also stay constant until it breaks. What I didn't understand is, when an observer in unprimed K wants to account for the breaking of the string using length contraction he should observe the unstressed length of the string be shortened by the lorentz factor, which I would argue means primed K should measure the unstressed rest length.
Now if that is true and I haven't done an error in my thinking so far, how do we know the unstressed rest length stays constant (I hope this is a better way to put the question)?
What I think you are trying to describe here is having both ships follow hyperbolic worldlines that are centered on the same point, which means the ship in front will have less proper acceleration than the ship in the rearYes
I assume this is for the alternate scenario you proposed, correct?Actually no, with the ratio of the proper time I mean the following (now I am referring to the minkowski diagram in the insight post): Calling the intersection between the simultaneity line of primed K with the left worldline event A and the intersection with the right worldline event B, the proper time from event (coordinates as given in unprimed K) (0|c[SUP]2[/SUP]/α) to event A along the left worldline is computed and similiary the proper time from event (0|c[SUP]2[/SUP]/α+L[SUB]0[/SUB]) (L[SUB]0[/SUB] means distance of the spaceships in unprimed K) to event B along the right worldline is computed and the ratio between the latter and the former proper time yields when taking the first order approximation τ[SUB]B[/SUB]/τ[SUB]A[/SUB]=1+αL[SUB]0[/SUB].
Writing these lines I guess for small velocities of the left spaceships both scenarios don't significantly differ when it comes to the distance between both spaceships in primed K and the proper time along the paths, which is why talking about Bell's scenario also justifies using the equivalence principle in this way (?).
I assume here you mean the original Bell spaceship scenario, correct? If so, no, the scenario is set in flat spacetime so there is no tidal force.Yes and I was asking the question because my poor understanding of the equivalence principle made me think an accelerating observer will justify him being at rest, despite feeling proper acceleration, via a gravitational field, so that from an accelerating observer's perspective there's automatically spacetime curvature and other general relativistic effects involved, but this is only what I expected from reading popular science articles (I should probably wait until I learn the math needed to get into general relativity before randomly asking questions based on speculation).
Thanks already for your great help!
You can't say this, because the two ships blast off simultaneously according to both shipsA recent post I made looking at clock synchronisation and simultaneity (also looking at one way speed of light) seemed to suggest that it is impossible to prove simultaneity without assuming the speed of light is isotropic as there is no physical test that can be made to prove it. So if that logic applies, then it must equally apply to this paradox in so much as it must be impossible to say which ship moves first. So it must be impossible to say why the string breaks.
Actually, you can say that, and be perfectly correct– it's all a question of reference frame. In the frame that the two spaceships end up in, assuming they accelerate rapidly and reach a final cruising speed, what you will see is two spaceships moving toward you, back end first, some distance L apart. Then the engine at the front fires, breaking the rope, and then the engine at the back fires. The two ships then slow to a stop in your frame, by which point they are not only farther apart than L, they are also farther apart than an un-length-contracted rope could span– which explains why the rope had to break. This is a perfectly good explanation of "why" the rope breaks: "because the rocket in front fired first, which caused the distance between the rockets to stretch farther than the decelerating rope could span without breaking." It's all a question of reference frame, no one's frame gets to talk about "absolute simultaneity."
Simultaneity is never anything but a coordinate system, and we can choose our coordinates to say "what happened" in a completely arbitrary way. There isn't even a "reference frame of the rockets", because a reference frame is something local– language like "the reference frame of the rockets" is actually a coordinate system, not a reference frame, though this distinction is often blurred in special relativity. A reference frame should really mean "a perspective from which to make an observation", not a global coordinate system, though this distinction isn't really my point– my point is, "why" answers should avoid being interpreted as reifying some coordinate system.
one can even say it is "because the forward ship blasts off first,"You can't say this, because the two ships blast off simultaneously according to both ships; their clocks are synchronized in the original rest frame, and remain so until the instant they blast off, and that instant is stipulated to be the same instant, in the original rest frame, for both ships.
Since forces are involved, why does the rest length of the string stay the same in the K'?It doesn't; it increases. The length of the string stays the same in the original rest frame, K (no prime), but the string is not at rest in that frame once the ships start accelerating.
Replacing the second spaceship with one whose proper acceleration has a different value, namely one corresponding to a hyperbolic worldline (where the center of the hyperbola is located in the origin), will the distance between the spaceships in K' now be constant?In the scenario as given, both spaceships are following hyperbolic worldlines–but the hyperbolas are centered on different points. What I think you are trying to describe here is having both ships follow hyperbolic worldlines that are centered on the same point, which means the ship in front will have less proper acceleration than the ship in the rear. In this case, yes, the distance between the ships (and therefore the length of the string) in K', the momentary rest frame of the string, will be constant. And in the original rest frame, K (no prime), the distance between the ships will decrease (because the one in the rear is accelerating more and so catching up to the one in front).
In a relativity book I am reading a connection is drawn to the equivalence principle by showing that in K' the proper time of the second spaceship is ahead of the first one's proper time by the amount expected using the weak field formula for gravitational time dilation (when considering the first order approximation of the ratio of each spaceships proper time).I assume this is for the alternate scenario you proposed, correct? (In other words, the one in which the front ship has less proper acceleration than the rear ship, and the distance between them in K' remains constant.) If so, yes, this is a standard method for describing the equivalence principle, and the "rate of time flow" of the two ships differs accordingly. But this only works because the ships remain a constant distance apart in K'. It wouldn't work for the original Bell spaceship scenario, the one described in the Insights post.
This makes me curious whether using the equivalence principle the increasing distance in K' would be attributed to tidal force?I assume here you mean the original Bell spaceship scenario, correct? If so, no, the scenario is set in flat spacetime so there is no tidal force.
What I think this "paradox" is best at bringing out is that there really does not exist a "correct" language to say "why" the string breaks. The physics prediction is only that the string breaks– the why question simply does not have a unique answer. One can say it is "because of length contraction", one can say it is "because of the equivalence principle", and one can even say it is "because the forward ship blasts off first," etc., it all depends on the reference frame chosen. This is natural– we don't answer physics questions about "why" until after we choose a reference frame, indeed I would argue that the main reason we choose reference frames in the first place is to be able to create a language capable of answering "why" questions at a more experiential level. Since relativity is the one place where we advance a certain agnosticism about reference frames, this gives "why" questions an especially interesting status there.
Thanks for the very well written Insights.
I put the beginning of my own SRT FAQ online now. It's not finished (only the kinematic part is nearly finished (I need to add a section on the socalled twin paradox) and the particle motion in an external field (also there I still have to write a section on Hamilton's principle and on the BMT equation discussing the Thomas precession). On the other hand, perhaps it's good when I get input from the forum before I put it (perhaps in several parts) also into the Insights section. You find a discussion of Bell's spaceship paradox (which of course is not a real paradox as all the socalled paradoxes of SRT) also there:
http://fias.uni-frankfurt.de/~hees/pf-faq/srt.pdf
PS: The idea to draw two grids for the two inertial frames is also great; I draw instead the hyperbolas of constant Minkowski "distances" 1, 2,… from the origin, but looking at your Minkowski diagrams, maybe the two linear grids are a better way, once one has explained the construction of the unit temporal and spatial distances with the hyperbolas first.
Great article and since I am trying to get my head around this seeming paradox I found this insight to be very useful to get an overview. Nonetheless I would like this opportunity to ask a few additional questions:1. Since forces are involved, why does the rest length of the string stay the same in the K'? 2. Replacing the second spaceship with one whose proper acceleration has a different value, namely one corresponding to a hyperbolic worldline (where the center of the hyperbola is located in the origin), will the distance between the spaceships in K' now be constant? 3. In a relativity book I am reading a connection is drawn to the equivalence principle by showing that in K' the proper time of the second spaceship is ahead of the first one's proper time by the amount expected using the weak field formula for gravitational time dilation (when considering the first order approximation of the ratio of each spaceships proper time). This makes me curious whether using the equivalence principle the increasing distance in K' would be attributed to tidal force? I would be grateful for any help regarding one of the questions.Also thanks to all participants for the well written article.