Limit Definition and 999 Threads
-

Graduate Is there a theoretical min. size/mass limit to a black hole?
Normally a star with a mass several times that of the sun will become a black hole at the end of the lifetime of that star. Can black holes exist with a mass much smaller than that exist? In other words, are black holes with a mass of Jupiter or even Earth exist? Or even much smaller than that...- DDH
- Thread
- Black hole Hole Limit Theoretical
- Replies: 9
- Forum: Astronomy and Astrophysics
-

What is the likely limit of processing speed?
the other thread about computer sciences got me wondering just how fast or how many millions or billions of tasks are likely to be the physical limits to processors? I'm not asking how small things will get but where if any is the brick wall to processing. to further limit the scope this is...- dragoneyes001
- Thread
- Computers Limit Processing Speed
- Replies: 10
- Forum: Programming and Computer Science
-
MHB Evaluating a Limit: $\lim_{x\to 0}\frac{1}{4}$
Evaluate $$\lim_{{x}\to{0}}\frac{\sqrt{1+\tan\left({x}\right)}-\sqrt{1+\sin\left({x}\right)}}{{x}^{3}}=\frac{1}{4}$$ I tried but didn't know how to deal with the undefines -
S
MHB Proving the Limit of an Infinite Sum
Prove that$\lim_{{n}\to{\infty}}\sum_{j=0}^{n} {n \choose j} \frac{{(x-a)}^{n+j}}{(n+j) !} = 0 $ thanks Sarrah -
S
Undergrad Finding derivative of x^x using limit definition
I am trying to find the derivative of x^x using the limit definition and am unable to follow what I have read. Can someone help me understand why lim [(x+h)^h -1]/h as h ---> 0 = ln(x). This part of the derivatio- scottshannon
- Thread
- Definition Derivative Limit Limit definition
- Replies: 2
- Forum: Calculus
-
C
Graduate Evaluating a limit of a function of two variables
I want to evaluate \displaystyle\lim_{(x,y)\to(-1,0)}\frac{y^4(x+1)}{|x+1|^3+2|y|^3} With some help, I was able to prove that the limit is 0, using Hölder's inequality. Like this: \left(|x+1|^3\right)^{1/5}\left(\frac{1}{2}|y|^3\right)^{4/5}\leq\frac{1}{5}|x+1|^3+\frac{4}{5}\frac{1}{2}|y|^3...- Cristopher
- Thread
- Function Limit Limits Variables
- Replies: 1
- Forum: Topology and Analysis
-
Y
Quick Limit Question (Pictures Included)
Hey all! I'm just going back through an old calculus book I have, and while attempting one of the odd numbered problems (because I can check my answers, obviously) I came across a problem and I'm not entirely sure if I've made a serious mistake and completely goofed, or if my book is incorrect...- Yawzheek
- Thread
- Limit
- Replies: 4
- Forum: Precalculus Mathematics Homework Help
-

Graduate Computing Entanglement Entropy of CFTs in the Large-c Limit
Consider the problem of computing the entanglement entropy of two CFTs in the thermofield double state on identical finite intervals in 1+1 dimensions. The Euclidean path integral is then equivalent to computing the 2-point twist correlator on a torus. Given a central charge ##c##, does anyone...- WannabeNewton
- Thread
- Computing Entanglement Entropy Limit
- Replies: 2
- Forum: Quantum Physics
-
C
Undergrad Precise definition of the limit (epsilon-delta)
Sorry, I am really struggling with the precise definition of the limit. I have a specific question I'm trying to work out lim(x->2) (4x2+2)=18 skipping the introduction part any advice? I am just not sure how to get rid of the 2 value to re-arrange |(4x2+2)-18| to look like |x-2| |x-2|<delta... -
C
Graduate Using the precise definition of a limit (epsilon & delta)
I'm trying to practise, precise definition of a limit (epsilon & delta) Just to check I'm along the right lines here's a previous question to the one I'm stuck on If epsilon > 0 then there is delta >0 ... All that introduction stuff, then Lim x-> 2 (3x-1) =5 Hence |x-2| < delta then |3x - 6|... -
O
MHB Limit of upper semicontinuous function
for any upper semi continuous how we can take limit ? limit or limsup ? which one is true ?- ozkan12
- Thread
- Function Limit
- Replies: 1
- Forum: Topology and Analysis
-

Limit does not exist but function exist
Homework Statement there are four cases on limits given to us, and one of them I didnt really understand. This case was: Limit f(x) as x approaches a does not exist but f(a) exist. Homework Equations The Attempt at a Solution My answer here that the limit in this piecewise defined function...- funlord
- Thread
- Function Limit
- Replies: 6
- Forum: Precalculus Mathematics Homework Help
-
C
Undergrad How can I find the limit 0/0 when using direct substitution?
I am really struggling with limits at the moment. Any help would be great! Thanks to anyone in advance if they take the time to read the rest of this. Basically i am struggling with finding the limit when using direct substitution provides 0/0 I (think) am fine with limits that involve quadratic... -
H
Undergrad Speed of Light Limit: Factors & Vacuum Conditions
Under Ideal conditions (a vacuum and no gravity) what is the limiting factor or factors for the speed of light ? Thank you, Pat Hagar -

Undergrad Is a Very Large Number the Same as Infinity?
We know, 1/0.1=10; 1/0.01=100; 1/0.001=1000; 1/0.0001=10000; . . . 1/0.00000000001=100000000000 . . . 1/0=infinity Why is it not correct?- Md. Abde Mannaf
- Thread
- Limit
- Replies: 17
- Forum: General Math
-
C
Undergrad Understanding a Step in Finding a Limit: Lim(x->0) x.sqrt(x+2) / sin(x)
Apologies if this is in the wrong place. I'm struggling to understand a step in finding a limit Lim(x->0) x.sqrt(x+2) / sin(x) Following the given solution I get to the point where it's all divided through by x to give Sqrt(x+2) / sin x/x Which as approaching 0 gives Sqrt(2) / 1 = sqrt(2)... -

Graduate Non-relativistic limit of Dirac bilinear
Hi, I'm studying direct detection techniques for dark matter and in almost all the articles I read (e.g. Gondolo, P. (1996, May 13). Phenomenological Introduction to Direct Dark Matter Detection. arXiv.org.) the authors say that in the non-relativistic limit the vector and axial currents take...- Andrea M.
- Thread
- Dirac Limit
- Replies: 3
- Forum: High Energy, Nuclear, Particle Physics
-
L
Graduate Convergence of improper integrals
What is the difference between \int_{-\infty}^{\infty} \frac{x}{1+x^2}dx and \lim_{R\rightarrow \infty}\int_{-R}^{R} \frac{x}{1+x^2}dx ? And why does the first expression diverge, whilst the second converges and is equal to zero? -
B
MHB Can the limit of (x,y) at (1,0) be found using l'hopital's rule?
I am trying to find the limit of the following: lim(x,y)--> (1,0) ((x-y-1)2/(x+y-1)2) I have had a few attempts trying to use l'hopital's rule but i don't seem to be getting anywhere...- brunette15
- Thread
- Limit
- Replies: 1
- Forum: Calculus
-
S
Limit problem simplify the root
Homework Statement [/B] I feel like I'm missing some theorem which is preventing me from finalizing this problem! It's been driving me nuts I feel like I'm missing something super basic! Ultimately they've given the solution, g/8, so I know this is how I should try to get the equation to look...- StrSpeed
- Thread
- Limit Root Simplify
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
B
MHB Problem evaluating the limit to find the radius of convergence
Hi everyone, I am trying to evaluate the radius of convergence for the following power series: (k!(x-1)k)/((2k)(kk)) I have begun by trying to compute L = lim k-->inf (an+1/an). To then be able to say R = 1/L. So far i have L = lim k--> inf (kk(k+1)!)/(2(k+1)k+1k!) From here i am having...- brunette15
- Thread
- Convergence Limit Radius Radius of convergence
- Replies: 2
- Forum: Calculus
-
B
MHB What is the connection between the natural logarithm and the limit of a series?
I am attempting to solve the limit for the following series: -1 + 1/2 - 1/3 + 1/4 ... (-1)^n/(n+1) I am able to determine that the series converges by applying the ratio test however i am having trouble evaluating the limit itself :/- brunette15
- Thread
- Limit Series
- Replies: 1
- Forum: Calculus
-
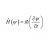
Undergrad Limit of Series: $\frac{1}{n}$
What should be the limit of the following series (if any ...) \frac{{1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{n}}}{n}- Vitor Pimenta
- Thread
- Limit Series
- Replies: 5
- Forum: Calculus
-
A
Graduate Why c Speed Limit Doesn't Prove Space is Continuous?
Hi everyone, First of all thank you for all the amazing amounts of information on this forum! I have a very stupid question, which is probably due to a deep misunderstanding about space quantization. I was wandering why the fact that no mass could move at the speed of light is not per se a...- Andrea Panza
- Thread
- Continuous Limit Space Speed
- Replies: 11
- Forum: Special and General Relativity
-
T
MHB Limit as x approaches negative infinity.
For this function: $$\lim_{{x}\to{-\infty}}\frac {x} {\sqrt{x^2}} = -1$$ Why is this correct? If x is equal to -1, for example, -1 square is 1. And the square root of 1 is 1. So should the answer be 1? -
N
Why doesn't the limit exist for this function at (0,0)?
Homework Statement I have to show that the following function does not have a limit as (x,y) approaches (0,0) The Attempt at a Solution I tried taking different paths for example y=x or y=0 and switching to polar coordinates, but I don't get anywhere.- NanoMath
- Thread
- Limit
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-

MHB How could we calculate the limit?
Hello! (Wave)Let the (linear) differential equation $y'+ay=b(x)$ where $a>0, b$ continuous on $[0,+\infty)$ and $\lim_{x \to +\infty} b(x)=l \in \mathbb{R}$. Show that each solution of the differential equation goes to $\frac{l}{a}$ while $x \to +\infty$, i.e. if $\phi$ is any solution of... -
N
High School Could someone please explain what a limit is?
I've been searching around trying to understand them. About to take calculus and I want to be prepared. Could someone explain what they are and give a few typical limit problems and solve them Thank you -
W
Graduate Understanding the Epsilon Delta Definition of a Limit
Hi I'm new to limits and calculus in general. Our professor told us there existed some rigorous proof for a limit, but it was "beyond the scope of the course". All we needed to know about a limit was that (1)$$\lim_{x\to a} f(x)$$ is true iff when x approaches a from both directions p(x)...- WhyNerfZed
- Thread
- Definition Delta Epsilon Epsilon delta Limit
- Replies: 6
- Forum: Calculus
-

Graduate Angular distribution of radiation in relativistic limit
While linear accelerating an electron, with direction of acceleration being the ##z+## axis of the spherical coordinates, its radiation in angular distribution form is(according to this tutorial: http://farside.ph.utexas.edu/teaching/em/lectures/node132.html) ##\frac{dP(t')}{d\Omega} =...- genxium
- Thread
- Angular Distribution Limit Radiation Relativistic
- Replies: 9
- Forum: Thermodynamics
-
A
Does the Limit of sin(n*alpha) as n Approaches Infinity Diverge?
Homework Statement Show that lim n->inf sin(n*alpha), 0 < alpha < pi, diverges. Homework Equations lim n-> inf sin(n) diverges The Attempt at a Solution I know how to solve this for a constant value of alpha (i.e pi/3), but am unaware of solving this one, where alpha may vary. I know that...- AndrejN96
- Thread
- Limit
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
U
Period of Limit Cycle: Find B for Hopf Bifurcation
Homework Statement I'm given this system: \dot x = Ax^2 y + 1 - (B+1)x \dot y = Bx - Ax^2 y (a) Find the value of B when hopf bifurcation occurs. (b) Estimate the period of the limit cycle in terms of ##A## and ##B##.Homework EquationsThe Attempt at a Solution I have found fixed point to be...- unscientific
- Thread
- Cycle Dynamical systems Limit Period Physics homework
- Replies: 23
- Forum: Advanced Physics Homework Help
-
B
What is the relationship between reabsorption and heating in laser cooling?
Homework Statement I have to study laser cooling. I'm actually trying to understand the Doppler limit on temperature. On the net I have found "at a certain point the cooling mechanism is foiled by heating due to the random absorption and reemission of photons...- bznm
- Thread
- Cooling Doppler Laser Limit
- Replies: 1
- Forum: Advanced Physics Homework Help
-
T
Why Does the Limit of (n! / n^2) Approach Infinity?
Homework Statement So, I'm doing a series problem, and after applying the root test I end up with the following limit: Lim as n--> inf of (n! / n^2) = infinity according to the solution manual. I can't seem to understand this because the way I look at it, each term in the numerator is...- ThatDude
- Thread
- Confused Limit
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-

MHB What are limit tests and how do they establish convergence of a series?
I've just studied integral tests for convergence, 1st timer, but some detail is escaping me. The text reads: 1. Show that if $ \lim_{{n}\to{\infty}} {n}^{p}\: {U}_{n}\implies A \lt \infty\: (p \gt 1) $ Then $ \sum_{n=1}^{\infty} {U}_{n}\: $ converges 2. Show that if $ \lim_{{n}\to{\infty}} n... -

Propability of finding a particle outside the classical limit
Homework Statement I'm asked to calculate the propability of finding a particle outside the classical limit for a quantum harmonic oscillator in it's ground state Homework Equations Ψ0(x) = a*emωx2/2hbar When a = (mω/πhbar)1/4 The ground state energy E0 =hbar*ω2/2 The Attempt at a Solution I...- Noctisdark
- Thread
- Classical Limit Outside Particle
- Replies: 1
- Forum: Advanced Physics Homework Help
-
P
Limit as n->infinity of (n^n)/n
Homework Statement Evaluate the limit ##\lim_{n\to\infty} \dfrac{n^n}{n!}## Homework Equations Ratio test: ##a_{n+1}*\dfrac{1}{a_n}## The Attempt at a Solution I was having trouble evaluating this so I tried to use the ratio test which unfortunately leads to ##\lim_{n\to\infty}...- Potatochip911
- Thread
- Limit
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-

Graduate "Speed limit of light" analogy
Thought of this while driving home from the lofters. As if we need one more analogy for relativistic speed limits, but here goes... Q: How is c a speed limit? Why can't we just go a little faster and exceed it? A: Behold an analogy as to how geometry can limit movement, no matter how fast you...- DaveC426913
- Thread
- Analogy Light Limit
- Replies: 9
- Forum: Special and General Relativity
-
P
Solve Limit at Infinity: $(-1)^n \sqrt{n+1}/n$
Homework Statement $$\lim_{x\to\infty} \dfrac{(-1)^n\sqrt{n+1}}{n}$$ Homework Equations 3. The Attempt at a Solution [/B] This is what I managed to do but I just wanted to verify that this is the correct way of solving it, I'm mainly concerned about the fact that I took the absolute value...- Potatochip911
- Thread
- Infinity Limit Limit at infinity
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
W
Find the limit of the given sequence
Homework Statement Find the limit of the given sequence as n →∞ Homework Equations (1+n^2)^(1/ln(n)) The Attempt at a Solution Wolfram said the answer was e^2, though i cannot figure out why. Any help would be greatly appreciated.- whattheheckV
- Thread
- Limit Sequence
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
R
Evaluating limit of floor function
Homework Statement How $$ \lim_{x\to\infty} \frac{nlogx}{[x]} = 0 $$ ? Here n∈ ℕ Here [x] is greatest integer or floor function of x. Homework Equations [x] = x - {x} where {x} is fractional part of x. The Attempt at a Solution I know floor function is not differentiable. We are getting here...- Raghav Gupta
- Thread
- Function Limit
- Replies: 13
- Forum: Precalculus Mathematics Homework Help
-
J
Now you can take the limit as ##z## approaches ##-1##.
Homework Statement Calculate the following limit if it exists ## \lim_{z\to -1}\frac{\sqrt{z}-i+\sqrt{z+1}}{\sqrt{z^2-1}} ## the branch of root is chosen so that ## \sqrt{-1}=i## Homework EquationsThe Attempt at a Solution I tried most of the same things that I tried earlier today (...- jjr
- Thread
- Complex Limit
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
J
Calculate Limit: \lim_{z\to i} \frac{z^3+i}{z-i}
Homework Statement Calculate the following limit if it exists: ##\lim_{z\to i} = \frac{z^3+i}{z-i}## Homework Equations Possibly relevant: ## \lim_{z\to\infty} f(z) = \omega_0 \hspace{5mm} \text{if} \hspace{5mm} \lim_{z\to 0} f\left(\frac{1}{z}\right) = \omega_0## The Attempt at a Solution...- jjr
- Thread
- Complex Limit
- Replies: 23
- Forum: Calculus and Beyond Homework Help
-
S
MHB Solving Limit of Question with Given Solution -3/2
Hi, I need help with the following limit, the solution is apparently -3/2 but I don't get it. Question: limit as n approaches infinity of [ sqrt(n^2 +3n - 4) - sqrt(n^2 + 6n +5) ] Attempt: So I was just thinking to factor out n like: (n^2)^(1/2) (1 + 3/n - 4/n^2)^1/2 - n (n^2)^(1/2)... -
R
Evaluating a limit as x tends to ## \infty##
Homework Statement $$ \lim_{x\to\infty} (\sqrt{a^2x^2 +bx + x} -ax) = $$ b/2a b/a 0 2b/a Homework Equations Lim x tends to infinity 1/x = 0 The Attempt at a Solution Taking a2x2 common from square root, we get $$ \lim_{x\to\infty} (ax \sqrt{1+\frac{b}{a^2x}+ \frac{1}{a^2x}} -ax) = $$...- Raghav Gupta
- Thread
- Limit
- Replies: 20
- Forum: Precalculus Mathematics Homework Help
-
S
Limit of (3/4)^(n+1) as n approaches infinity
Hello, I was just wondering how to solve this limit: Limit of (3/4)^(n+1) as n approaches infinity My attempt: (3/4)^(n+1) = (3^ (n+1) ) / (4 ^ (n+1)) Top goes to infinity and bottom goes to infinity to use l'hopital rule. lim = ( ln(3) * 1 * 3^(n+1) ) / ( ln(4) * 1 * 4^(n+1) ) But the...- seal308
- Thread
- Infinity Limit
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
S
MHB Limit of (3/4)^(n+1) as n approaches infinity
Hello, I was just wondering how to solve this limit: Limit of (3/4)^(n+1) as n approaches infinity My attempt: (3/4)^(n+1) = (3^ (n+1) ) / (4 ^ (n+1)) Top goes to infinity and bottom goes to infinity to use l'hopital rule. lim = ( ln(3) * 1 * 3^(n+1) ) / ( ln(4) * 1 * 4^(n+1) ) But the... -
O
Undergrad Limit on Faraday's cage (rearranging charges)
Having a question regarding Faraday's cage,Applying a magnetic field over the cage, will cause the charges in the conducting cage to rearrange, thus causing another field which opposes the first field. This will give a net field inside the cage of zero (this is why we are safe in a car during a...- olu
- Thread
- Cage Charges Limit
- Replies: 1
- Forum: Electromagnetism
-
R
Undergrad Converting a limit to integral form or vice-versa
What is the proof for this $$ \int_a^b f(x) dx = 1/n\lim_{n\to\infty} (f(a) + f(a+h) + f(a+2h) +...+ f( a+ (n-1)h)) $$ h = (b-a)/n Also I think there is some summation form which can be converted to integral form how?- Raghav Gupta
- Thread
- Form Integral Limit
- Replies: 15
- Forum: Calculus
-
Y
What is the Limit of a Floor Function at an Arbitrary Point?
Homework Statement The function f is defined f(x)=floor(x^2)/x^2 I need to find the limit of the function at an arbitrary point. For the continuous parts it was fine, and also for right sided limit at positive points of discontinuity (and left sided for negatives, for all of which the lim is...- Yoni V
- Thread
- Function Limit
- Replies: 2
- Forum: Calculus and Beyond Homework Help