Learn All About Earth’s Gravity

Earth’s gravitational field at the surface is approximately 9.8 Newtons/kilogram or 9.8 meters/second/second. But how does that change due to its shape, rotation, composition, and various locations along its surface and interior? This article will answer those questions.

Earth’s Gravity Key Points

1. Earth’s gravitational field at the surface is approximately 9.8 Newtons/kilogram.
2. The deviation in Earth’s surface gravity due to latitude is about 0.7%.
3. The variation due to local density and topography of the land is about 0.02%.
4. The geoid is the hypothetical shape the Earth would take if its surface were completely covered in the ocean.
5. The gravitational field increases as you go deeper into the Earth, reaching a local maximum of about 10.6 meters/second/second about halfway between the center and the surface.
6. There is no latitude-dependent time dilation due to relativistic effects.
7. Knowledge about Earth’s gravity comes from satellites, geographers, surveyors, and earthquake arrival times.

Latitude dependence due to Earth’s shape and rotation

One can simply calculate the centripetal acceleration at Earth’s equator, given by (6378 km) x (2$\pi$/24 hours)$^2$, and see that it is roughly one part in three hundred of Earth’s average gravitational field. This leads to an expectation that on a spherically symmetric but rotating Earth, the apparent gravity varies due to the centrifugal force by 0.3%. The picture, however, is slightly more complicated and the variation is slightly stronger.

The Earth is not incompressible, and its rotation has caused it to bulge at the equator, such that its radius at the equator is 6378 km and its radius pole-to-pole is 6356 km. The farthest point from Earth’s center is not Mt. Everest, but Chimborazo in Ecuador. Earth’s shape can be described as an oblate spheroid where the gravitational field deviates from the mean with latitude according to the relation $1-3\cos^2\theta$, and combining the effect of the bulge and the rotation, the total variation in Earth’s surface gravity due to latitude is about 0.7%.

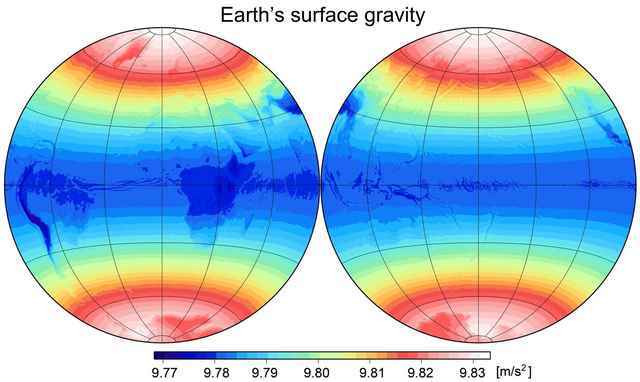
Earth’s absolute surface gravity variation. It mainly varies due to latitude and a little bit due to topography.

Anomalies from rock density and topography

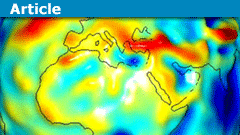
The Earth is more than just a uniform oblate spheroid. Further deviations from symmetry can be described with additional spherical harmonic terms. After these are taken into account, there are variations in Earth’s surface gravity due to the local density and topography of the land. These tend to be an order of magnitude weaker compared to the latitude dependence, on the order of 0.02% deviation from the mean. Looking at a map of these anomalies, it is clear that they tend to be strongest around mountain ranges and geological hotspots, and also a weak spot in the ocean near Sri Lanka the origin of which I do not know.

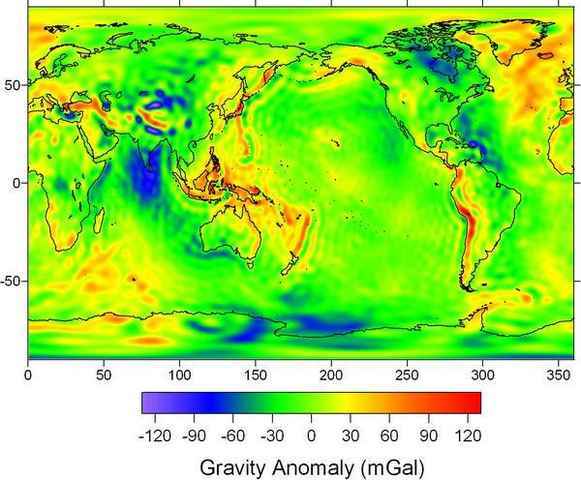
A map of Earth’s gravity anomalies, which is roughly what remains when you account for its rotational bulge. The unit “Gal” is 1 cm/s/s, so the difference between red and blue is about 0.0002 g. Source.

It has become common practice to present maps such as the ones above when discussing Earth’s gravity, but really the variation due to latitude shown in the first image is much stronger.

The Geoid

The geoid is the hypothetical shape that the Earth would take if its surface were completely covered in the ocean, such that the gravitational and centrifugal potential is the same at every point on the surface. It is actually at this surface that the sea level is defined. Its shape is generally described in terms of spherical harmonics, with a greater and greater number of terms being used as more precise data becomes available. Relevant xkcd.

 

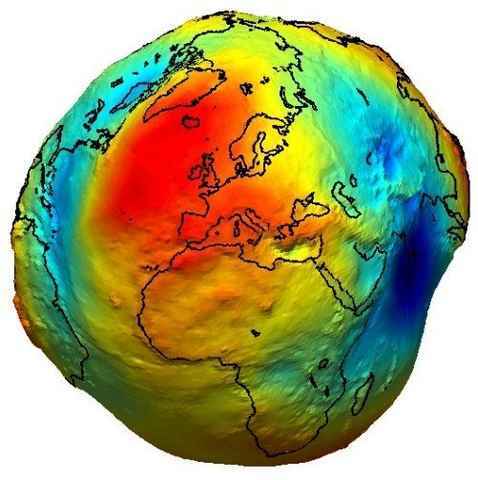
An example of an Earth geoid. The scale is exaggerated, I doubt anyone could squint-deduce that the Earth is not spherical. Source.

Gravity in Earth’s interior

In addition to knowing the gravitational field at different points on the surface, we also have information about how the gravitational field changes as you go deeper toward the center of the Earth. Within a spherically symmetric mass, the shell theorem tells us that only the mass enclosed below our current radius matters and that anything “above” us does not contribute to the gravitational field. A naive assumption of a uniformly dense Earth would imply a linearly decreasing gravitational field. Looking at the interior profile of the Earth, there are two layers of high-density core, a sharp discontinuity in density at the mantle, and then the crust and oceans. Because the discontinuity at the core-mantle boundary is so sharp, the gravitational field increases as we look deeper into the Earth, getting closer to a higher-density sphere. It reaches a local maximum of about 10.6 meters/second/second about halfway between the center and the surface.

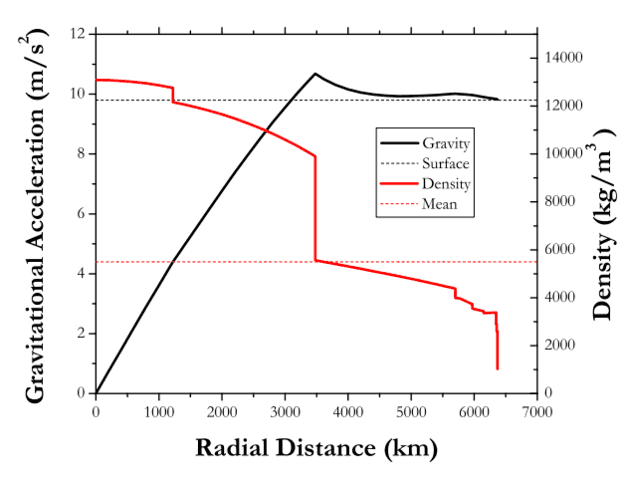
The density (red) and gravitational field (black) as a function of the distance from Earth’s center. Because of the sharp discontinuity in the density at the core-mantle boundary, gravity increases as you go deeper. This is from the arxiv version of my paper.

Relativistic effects on Earth’s surface

This may be out-of-scope but I find it interesting.

When the atomic clock research group at the National Institute of Standards and Technology had created a sufficiently precise clock, they took two identical models and raised one of them about a foot higher than the other. They were able to observe the differences over time due to the differing gravitational potentials as predicted by Einstein’s general theory of relativity. If you consider a clock on the equator and a clock on one of the poles, what difference can you expect in the rate of ticking? The clock on the equator is moving faster than the one on the pole, so you might expect it to tick slower. However, it has a weaker gravitational potential, so you might expect it to tick faster. It turns out, the effects cancel for non-coincidental reasons and there is no latitude-dependent time dilation.

Naively, one could calculate the Lorentz factor between the pole and the equator, which is about $1+10^{-12}$, and also calculate the difference in gravitational time dilation at the polar and equatorial radius of the Earth. This is about $2\cdot10^{-12}$, so you can see that the two effects are in the same order of magnitude as the Lorentz factor but not naively the same.

The reasons that the two effects cancel are explained in this Socratic dialogue by S.P. Drake and laid out by Lubos Motl in a Stack Exchange post. The crux of the argument is that because the Earth’s surface is (roughly) stationary, it must have equal gravitational potential at all points, thus the time dilation relative to a free-falling observer (Lubos points out that a geocentric orbit would be a good reference frame in which to analyze this) must be the same at all points. An explicit calculation in Drake’s paper demonstrates, that the gravitational potential at the poles, and the gravitational plus centrifugal potential at the equator, are the same.

Research methods

How do we know all this information about Earth’s gravity? It started just by geographers and surveyors measuring the gravitational field as they explored the land. As an example, Canada’s first official astronomer and surveyor, Otto Klotz, whom I know of because he has the same last name as me (but no relation), traveled through the country around the year 1900 making gravity measurements with a pendulum as he went. Nowadays the more precise maps of Earth’s gravity come from satellites such as GOCE that use orbiting accelerators to map out the surface gravity and higher-order spherical harmonic contributions. The knowledge about Earth’s interior comes mainly from measuring earthquake arrival times at various locations and figuring out where seismic waves are reflected and refracted and how fast they’re going, although now satellite accelerometers can independently verify this.