Lessons From the Bizzaro Universe

The terms Bizarro and Bizarro World originated in Superman comics, where strangely imperfect versions of Superman, other action characters, and even Earth itself were conceived of, and provided the basis of stories.  And who can ever forget the Seinfeld episode entitled “Bizarro Jerry,” in which there are Bizarro versions of Jerry and all his friends?   But, unlike his group, the Bizarro versions are strangely nice, polite, and not self-centered.

In popular culture, Bizarro has come to mean an imperfectly flawed version of something else.  So I thought it might be fun to conceptually envision a Bizarro version of our own universe.  I also felt that we might gain some additional insight into the fundamental characteristics of our own universe by studying the Bizzaro universe.

Characteristics of the Bizzaro Universe

1.  Like the actual universe, the Bizzaro Universe is 4 dimensional, but, unlike the actual universe, the time dimension in the Bizzaro Universe is an actual spatial dimension.
2. For each 3D rest frame in the Bizzaro Universe, the time dimension (direction) is oriented perpendicular to that rest frame.   The 3D beings of the Bizzaro Universe cannot see into the time direction of their own rest frame, although, conceptually, they can see infinitely far in any of our other three spatial directions.
3. Each rest frame in the Bizzaro Universe is traveling through Bizzaro space-time at the very high characteristic velocity c (speed of light) into its own time direction.  The beings in this rest frame have no sense that this is happening since they cannot see into their own time direction.  However, they can see partially into the time directions of other frames of reference that are in relative motion….in a way.
4. All the clocks in each inertial frame of reference are synchronized with one another, although they may not be synchronized with the sets of clocks in other inertial frames of reference.
5. All inertial frames of reference in the Bizzaro Universe are rotationally offset with respect to one another by 4D rigid rotations.  To be more specific, the Bizzaro Lorentz Transformation (Borentz Transformation) in Standard Form for the Bizzaro Universe is given by:   $$x’=\frac{x-vt}{\sqrt{1+(v/c)^2}}\tag{1a}$$and $$t’=\frac{(t+vx/c^2)}{\sqrt{1+(v/c)^2}}\tag{1b}$$or equivalently $$x’=x\cos{\theta}-(ct)\sin{\theta}\tag{2a}$$and$$(ct’)=x\sin{\theta}+(ct)\cos{\theta}\tag{2b}$$with$$\sin{\theta}=\frac{(v/c)}{\sqrt{1+(v/c)^2}}\tag{3a}$$and$$\cos{\theta}=\frac{1}{\sqrt{1+(v/c)^2}}\tag{3b}$$

Eqns. 2 can readily be recognized as the usual transformation equations for a rigid rotation of the coordinate axes by an angle $\theta$.  It follows from Eqns. 1-3 that the Cartesian coordinate line element in the Bizarro Universe is given by:  $$(ds)^2=(dx)^2+(cdt)^2=(dx’)^2+(cdt’)^2\tag{4}$$

Unlike our actual universe which is non-Euclidean, the Bizzaro Universe is totally Euclidean.  This makes it much easier to draw space-time diagrams for the Bizzaro Universe.

I should also mention that the Bizzaro Universe is, in essence,   equivalent to the “loaf of bread” arrangement described in Brian Greene’s book, “The Elegant Universe.”  However, for whatever reason, Greene fails to make any distinction between his Euclidean loaf-of-bread description and our actual non-Euclidean universe.

The geometry of Bizzaro Universe

In the Bizzaro Universe, as with our own universe, we refer to events as points in space-time with coordinates (ct, x, y, z), although, in the Bizzaro universe, the coordinate ct is an actual spatial coordinate.  Let $\mathbf{s}$ represent a 4D position vector drawn from an arbitrary origin in Bizzaro space-time to an event (ct, x, y, z).  Since Bizzaro spacetime is Euclidean, we can represent this position vector in terms of Cartesian unit vectors by the equation:  $$\mathbf{s}=(ct)\mathbf{i_t}+x\mathbf{i_x}+y\mathbf{i_y}+z\mathbf{i_z}\tag{4}$$where $\mathbf{i_t}$ is the unit vector in the time direction.  (Note that, in all this, we are referring to the Cartesian coordinates of events, as referenced from an arbitrarily selected origin in 4D Bizzaro spacetime.)

Suppose that we next focus on a differential 4D position vector $\mathbf{ds}$ drawn between the two closely neighboring events at (ct,  x,  y,  z) and at (ct+cdt,  x+dx , y+dy, z+dz) in Bizzaro space-time (as reckoned from a rest frame of reference S).  The equation for this differential position vector is, of course, given by:  $$\mathbf{ds}=(cdt)\mathbf{i_t}+(dx)\mathbf{i_x}+(dy)\mathbf{i_y}+(dz)\mathbf{i_z}\tag{5}$$The length of this differential position vector is obtained by dotting it with itself:$$(ds)^2=\mathbf{ds}\centerdot \mathbf{ds}=(cdt)^2+(dx)^2+(dy)^2+(dz)^2\tag{6}$$Eqn. 6 can be recognized is just the 4D equivalent of the Pythagorean theorem.

Suppose now there is also a second frame of reference S’ (containing 3D beings traveling with 3D velocity components $v_x$, $v_y$, and $v_z$ relative to our first frame of reference S) and employing Cartesian event coordinates (ct’, x’, y’,z’).  If we resolve this same differential position vector $\mathbf{ds}$ into components with respect to the primed system of coordinates, we obtain:$$\mathbf{ds}=(cdt’)\mathbf{i_t’}+(dx’)\mathbf{i_x’}+(dy’)\mathbf{i_y’}+(dz’)\mathbf{i_z’}\tag{7}$$And, in terms of the primed coordinates, the length of the vector $\mathbf{ds}$ is given by:  $$(ds)^2=\mathbf{ds}\centerdot \mathbf{ds}=(cdt’)^2+(dx’)^2+(dy’)^2+(dz’)^2\tag{8}$$

Since the differential position vector $\mathbf{ds}$ does not depend on the specific coordinate system or frame of reference from which it is reckoned (i.e., it is invariant under a change in frame of reference), we must immediately conclude that:  $$\mathbf{ds}=(cdt)\mathbf{i_t}+(dx)\mathbf{i_x}+(dy)\mathbf{i_y}+(dz)\mathbf{i_z}$$$$=(cdt’)\mathbf{i_t’}+(dx’)\mathbf{i_x’}+(dy’)\mathbf{i_y’}+(dz’)\mathbf{i_z’}\tag{9a}$$and$$(ds)^2=(cdt)^2+(dx)^2+(dy)^2+(dz)^2$$$$=(cdt’)^2+(dx’)^2+(dy’)^2+(dz’)^2\tag{9b}$$

Eqns. 9 apply irrespective of the relative 3D velocities of the S and S’ frames of reference, or the rotational and translational offsets of the two coordinate systems.

Frames of Reference

In the present context, it is worthwhile being a little more precise about the term “frame of reference.”  A frame of reference is basically a 3D x-y-z spatial cut out of 4D spacetime.  The time direction t for this spatial 3D cut is oriented perpendicular to the 3 orthogonal Cartesian spatial directions of the frame of reference.  Therefore, the time direction in 4D spacetime for a frame of reference S basically defines the frame of reference.

The residents of the Bizarro universe are analogous to 2-dimensional beings trapped within a flat plane that is immersed in 3D space.  They have no access to the 3rd dimension, except for the 2D cross-section that they currently occupy.  This 2D cross-section may not be stationary in 3D space; it may be moving forward (unbeknownst to them) into the 3rd (time) dimension.  If so, as time progresses, they would be sweeping out all of 3D space, and would ultimately be able to sample all of 3D space with their planar cross-section.  However, at any one instant of time (according to their synchronized set of clocks), they would only have access to a single planar slice out of 3D space.

This is totally analogous to what the 3D beings of the Bizzaro Universe are actually experiencing in their 4D spacetime.   In their rest frame of reference, they are trapped within a specific 3D slice out of 4D spacetime.  This 3D slice is unique to the particular reference frame they occupy (i.e., their rest frame).  They have no access or vision into the 4th dimension, except for this 3D cut.  The cut is not stationary; it is moving forward (unbeknownst to them) into their own 4th (time) spatial dimension.  As time (measured by the synchronized clocks in their 3D reference frame) progresses, they are sweeping out all of 4D spacetime, and will ultimately be able to sample all of the 4D spacetime (at least the part into their future) with their moving 3D cut.  However, at any one instant of time, they only have access to their single 3D cut-out of 4D spacetime (a 3D panoramic snapshot).  Finally, different frames of reference in relative motion possess different 3D cuts and different time directions perpendicular to these 3D cuts.

Four-Dimensional Bizzaro Velocity

Arguably, the most important equation in the present development is Eqn. 9a, providing a relationship for a differential position vector in Bizzaro spacetime, as reckoned from the coordinate systems that are employed in two different frames of reference, S and S’:$$\mathbf{ds}=(cdt)\mathbf{i_t}+(dx)\mathbf{i_x}+(dy)\mathbf{i_y}+(dz)\mathbf{i_z}$$

$$=(cdt’)\mathbf{i_t’}+(dx’)\mathbf{i_x’}+(dy’)\mathbf{i_y’}+(dz’)\mathbf{i_z’}\tag{9a}$$This is the starting point for the development of equations for the Bizzaro 4D velocity vector.

Imagine that we are following the motion of a specific material particle or observer that is at rest in the S’ frame of reference, such that its spatial coordinates x’, y’, and z’ are held constant, and thus dx’ = dy’ = dz’ = 0.  For this object, Eqn. 9a becomes:  $$\mathbf{ds}=(c\mathbf{i_t}+v_x\mathbf{i_x}+v_y\mathbf{i_y}+v_z\mathbf{i_z})dt=c\mathbf{i_t’}dt’\tag{10}$$where, here, $\mathbf{ds}$ represents the displacement of the object over the time interval dt for frame S and dt’ for frame S’, and where $v_x=(\partial x/\partial t)_{x’,y’,z’}$, $v_y=(\partial y/\partial t)_{x’,y’,z’}$, and $v_z=(\partial z/\partial t)_{x’,y’,z’}$.  Eqn. 10 expresses the differential position vector for the motion of our particle or observer in terms of the unit vectors for the S’ frame of reference and also in terms of the unit vectors for the S frame of reference.  The relationships we have used here for the (3D) velocity components $v_x$, $v_y$, and $v_z$ for the S frame are consistent with how these components would be conventionally be determined (i.e., by taking the derivative of the particle’s coordinates with respect to time, holding the material particle constant).  This is sometimes referred to as the “material time derivative.”

If we take the dot product of Eqn. 10 with itself, we obtain:$$(ds)^2=(c^2+v^2)(dt)^2=c^2(dt’)^2\tag{11}$$ where $v^2=(v_x)^2+(v_y)^2+(v_z)^2$.  Taking the square foot of Eqn. 11 then yields $$dt=\gamma dt’\tag{12}$$with $$\gamma=\frac{1}{\sqrt{1+(v/c)^2}}\tag{13}$$where, in the present situation, dt’ represents the differential of Bizzaro proper time measured in the rest reference frame of the moving particle.  Note that, unlike our real universe where $\gamma$ is always greater than unity, in the Bizzaro Universe, $\gamma$ is always less than unity.

If we now substitute Eqn. 13 into Eqn. 10, we obtain the Bizzaro 4 velocity $\mathbf{V}$ of the moving particle:  $$\mathbf{V}\equiv \left(\frac{\partial \mathbf{s}}{\partial t’}\right)_{x’,y’,z’}=c\gamma \mathbf{i_t}+v_x\gamma  \mathbf{i_x}+v_y\gamma \mathbf{i_y}+v_z\gamma \mathbf{i_z}=c\mathbf{i_t’}\tag{14}$$

Eqn. 14 contains lots of valuable new information concerning the basic nature of 4D Bizzaro spacetime and the kinematics of motion.  Since $\mathbf{ds}$ represents a differential displacement vector, it would appear (according to the right-hand side of this equation) that, even though the particle under consideration is at rest within the S’ frame of reference, it is not truly at rest in Bizzaro spacetime; it is actually covering distance into the 4th (time) dimension t’ with a speed equal to the speed of light c.  In fact, all objects that appear to be at rest within the S’ frame of reference, as well as the S’ frame of reference itself, are actually moving in the t’ direction at this speed.

The 4 velocities vector $\mathbf{V}$ defined by Eqn. 14 can be interpreted physically as the velocity of the S’ frame of reference (and all objects at rest within the S’ frame of reference) with regard to spacetime itself.  That is, Eqn. 14 clearly suggests that it is valid to regard Bizzaro spacetime as stationary and absolute and to treat $\mathbf{V}$ as the 4D velocity of an object or observer in the S’ frame of reference relative to stationary 4D Bizzaro spacetime.

This interpretation is clearly not unique to the S’ frame of reference, since the above analysis could just as easily be repeated for any other frame of reference.  Thus, In general, all objects in the Bizzaro Universe are traveling at the speed of light relative to spacetime, but their directions through spacetime are different and are determined by the directions of their time arrows (unit vectors in the time direction), which are unique to each frame of reference.

The beings of the Bizzaro Universe might think to themselves, “how can we, as objects in the Bizzaro Universe, be traveling through spacetime at the speed of light, and yet not be aware that this motion is taking place?”  The answer is that they are all trapped within their own 3D slice out of 4D spacetime (i.e., their own rest frame of reference), and they cannot see into their time dimension.  Furthermore, any objects that are at rest (or nearly at rest) in close proximity to them are each traveling at virtually the exact same velocity as they are; therefore, they don’t sense any relative movement on the order of the speed of light. Finally, the ride is very smooth, since there are no bumps in the road.

It is possible to express the 4D velocity of an object relative to Bizzaro spacetime not only interns of the time unit vector for its own frame of reference (i.e., $c\mathbf{i_t’}$), but also in terms of the unit vectors for any other reference frame that is not accelerating.  Thus, from Eqn. 14, the absolute 4D velocity of a particle in the S’ frame of reference, expressed in terms of the unit vectors for the non-accelerating S frame of reference, is given by $$\mathbf{V}=c\gamma \mathbf{i_t}+v_x\gamma  \mathbf{i_x}+v_y\gamma \mathbf{i_y}+v_z\gamma \mathbf{i_z}\tag{14}$$Similarly, the passage of proper time for a moving object can be expressed in terms of the time displayed on the synchronized clocks in any other non-accelerating frame of reference by means of the equation  $$dt’=\frac{dt}{\gamma}\tag{15}$$These equations allow observers in any arbitrary non-accelerating frame of reference to formulate physical laws for the motion of objects not at rest in their own reference frame, without actually having direct access to clocks or meter sticks for the reference frame of the moving object.

The present results apply not only to objects moving at constant speed relative to inertial frames of reference.  They also apply to objects that may be accelerating.  One simply regards the instantaneous 4D absolute Bizzaro velocity of an accelerating object is equal to that of an inertial reference frame moving at the same velocity (i.e., a so-called co-moving inertial reference frame).  Thus, the 4D Bizzaro velocities of all objects in the Bizzaro Universe, including objects that are accelerating, have a magnitude equal to the speed of light, but,  for accelerating objects, the orientation of their time arrows (unit vector in time direction) change with the proper time.

Bizzaro Train

In Einstein’s famous special relativity train scenario, there is a train traveling down a long straight track at a constant speed v comparable to the speed of light.  One team of observers is strung out along the platform (S frame of reference), armed with a set of clocks all synchronized with one another in the platform/track/ground frame of reference, and a second-team strung out along the train (S’ frame of reference), also armed with a set of clocks, all synchronized with one another in the train frame of reference.  Our objective now will be to use what we have learned so far to see how this same train scenario plays out in the Bizzaro Universe.

Application of Eqn. 14 to the train scenario leads to the following relationships for the absolute 4 velocities of the platform P and train T with respect to stationary Bizzaro spacetime (in terms of the platform frame unit vectors):  $$\mathbf{V_P}=c\mathbf{i_t}\tag{15a}$$  $$\mathbf{V_T}=c\gamma\mathbf{i_t}+\gamma v\mathbf{i_x}\tag{15b}$$

Based on these equations, we have sufficient information to represent the motion of the platform and train through Bizarro spacetime schematically, via a spacetime diagram.  Fig. 1 shows the sequence of locations for a 3-car train at proper train clock times $t_1′<t_2′<t_3’$.

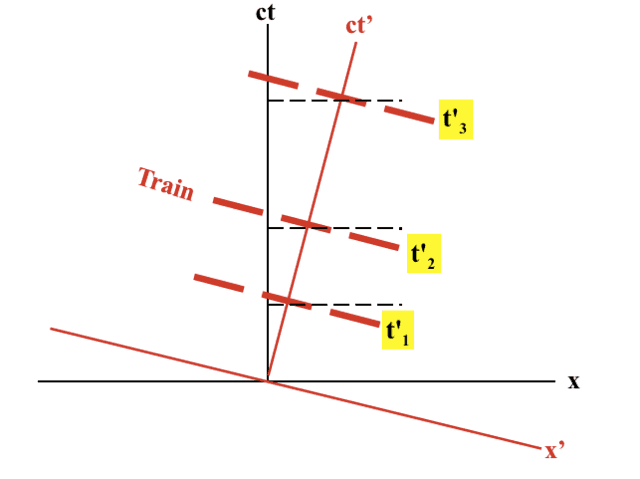
Figure 1. Train Movement Through Bizzaro Spacetime

The train is oriented parallel to the x’ axis and is moving at the speed of light (relative to Bizzaro spacetime) in the direction of the ct’ axis.  There is an observer on the train at location x’ = 0 (which corresponds to the center of the middle car).  The team on the platform focuses attention on this train rider and measures his relative speed using their own coordinate grid in the x-direction and their own set of synchronized clocks (displaying the time t which, incidentally, is not “proper train time” for objects at rest in the train).  They obtain $$v=\left(\frac{\partial x}{\partial t}\right)_{x’=0}\tag{16}$$This is the same relationship that would be obtained not only in the Bizzaro Universe but also in the real universe.  The entire train moves with this speed relative to the S reference frame, according to the measurement tools available to the observers in the S (platform) frame of reference.  However, this speed does not properly represent the true x component of the relative velocity vector of the train with respect to the platform in Bizzaro spacetime.  This is because it failed to take into account the difference between the proper train time and the platform clock time.  The actual relative 4 velocities of the train with respect to the platform is obtained by subtracting Eqn. 15 a from Eqn. 15 b, to yield:$$\mathbf{V_T-V_P}=c(\gamma-1)\mathbf{i_t}+\gamma v \mathbf{i_x}\tag{17}$$The component of this relative velocity vector in the t direction is not visible to the observers in the platform reference frame, since t constitutes their inaccessible time direction.  The component in the x-direction has an added factor of $\gamma$ to correct for the difference between the platform clock time t and the train proper time t’.

Fig. 2 is designed to provide some insight into the issues of simultaneity and length contraction (or expansion).

Figure 2  Simultaneity and Length Contraction/Expansion Assessment

The first question is, “What do the team of platform observers see when they look at the train at time t on their synchronized clocks?”  According to the figure, the rear end of the train arrives at platform time t first, at train time $t_1’$; later (in train time), the middle of the train arrives at platform time t, at train time $t_2’$; still later (in train time), the front end of the train arrives at ground time t, at train time $t_3’$.  Thus, at any specified time t on the synchronized platform clocks, the observers on the platform are able to view the entire train all at once.  However, unbeknownst to them, they are seeing the rear end of the train at an earlier train clock time t’ than the front of the train.  This result for the Bizzaro Universe is the opposite of what is found for the real universe.

With regard to length change, it appears from Fig. 2 that, in the Bizzaro Universe, the length of the train measured by the platform observers at time t will be greater than the train’s proper length in its rest frame.  This is the opposite of the length contraction effect observed in the real universe.

The final situation to be considered here will be the time dilation (or contraction) effect (Fig. 3).

Figure 3.  Assessment of Time Dilation/Contraction Effect

Fig. 3 shows the motion of the train rider situated in the middle of the train (x’=0) as he travels through Bizzaro spacetime.  He passes two observers on the ground at a distance of $\Delta x$ apart, and notes when he passes that the times displayed on their clocks differ by $\Delta t$.  He compares this with the corresponding time internal on his own clock $\Delta t’$, and determines that, for Bizzaro spacetime, $$\left(\frac{\Delta t’}{\Delta t}\right)_{x’=const}>1\tag{18}$$ This time expansion is exactly the opposite of the time dilation effect observed in the real universe.

Conclusion

It’s been interesting exploring the geometric and kinematic characteristics of the Euclidean Bizzarro Universe and making comparisons with the corresponding effects observed to take place in our own non-Euclidean universe.  Some of the analogies are enlightening and have provided some new insights and interpretations.  If anyone would be interested in continuing this pursuit, I would be interested in collaborating.  Other topics I would be motivated to analyze would be (1) constant acceleration kinematics, (2) paradoxes such as the pole paradox, and (3) Bizzaro laws of dynamics, such as momentum and energy conservation.