Learn the Amazing New Research on Untying Knots in Polymers

Polymer Key Points

1. The published paper studied how knots in polymers respond to an external flow field and how the knot affects the response of the polymer
2. Experiments and simulations of knotted polymer chains being stretched by an extensional flow field
3. The coil–stretch transition occurs when the flow is weak enough for the molecule to relax to a random coil
4. Simulations showed that knotted polymers stretch less at a given tension compared to unknotted polymers
5. Knotted polymers may require higher–than–expected flow to prevent them from contracting in bulk solutions
6. Experiments showed that knots can untie in multiple stages (up to five) and this was replicated in simulations
7. The Alexander Polynomial was used to track the evolution of the knot type in simulations
8. Experiments and simulations revealed that single–stage untying events were less common than expected

Macromolecules

A joint computational-experimental paper that I worked on was just published in MacroLetters, a journal that covers all topics relating to macromolecules (polymers and the like). In it, we looked at simulations of knotted polymer chains being stretched by an external flow field and studied how the knot affected the response of the polymer to the flow, and what happened to the knot if the flow wasn’t strong enough to keep the polymer stretched. Then, we compared it to data from my experiments looking at how knotted DNA molecules behave in similar fields, particularly looking at how the knots untie. While this Insight is specifically about this paper, I’ve written about my work in a few other articles, including a piece explaining the practical application of these DNA experiments a blog post on some of the more mathematical aspects, and one on my last pre-knot DNA paper.

 

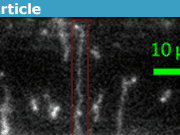
A stretched DNA molecule with a knot (near the left side of the molecule) that unties. This is the phenomenon investigated in this paper. The molecule is about 50 microns long when stretched.

We work in a lab that studies soft materials and is interested in the dynamics of polymers in a type of flow field called extensional (or elongational) flow, which is often used to characterize the dynamics of complex fluids. Planar extensional flow has fluid coming from two opposite directions and flowing out in two perpendicular directions. Test particles in the flow come in at high velocity, and the velocity in the initial direction decreases as the velocity in the perpendicular direction increases*.  In extensional flow, the velocity of the flow is proportional to position, and the proportionality constant is called the strain rate, which is the reciprocal of the time it takes for a test particle to increase its position by a factor of e. 

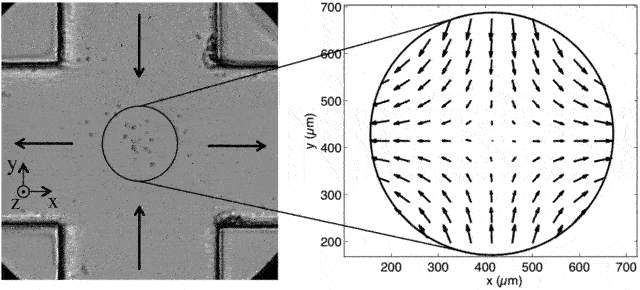
A cross-slot microfluidic device that gives rise to elongational flow (source). Objects coming from the top or bottom will have a y-velocity that decreases exponentially and an x-velocity that increases exponentially. (This isn’t from my experiments but it’s one of the better pictures available of what extensional flow is)

If instead of a test particle, you had a deformable object, it would get compressed in one direction while stretching in the perpendicular direction. A polymer is a sort of in-between a point particle and a squishy bulk object: when a polymer is in the middle of an extensional flow (the middle is called the stagnation point), it can have one end pulled one way and the other end pulled the other way. This makes it stretch, and it stretches until the drag forces from the flow are balanced by the internal entropic elasticity of the molecule. The molecule will stretch more if the flow is stronger, but this is a nonlinear effect: if the flow is weak enough, the molecule won’t stretch, it’ll just relax to a random coil. This is called the coil-stretch transition, and there is a critical strain rate at which it occurs.

A video from one of my experiments. DNA molecules follow the extensional electric field and move to the left and right. A molecule right in the middle gets has both ends pulled in opposite directions, and gets stretched to 50 microns long, about 70% of its full length.

Stretching knotted DNA molecules

I have been doing experiments stretching knotted DNA molecules in extensional fields**. I was trying to see how the knots behave at different levels of tension, so I’d start by stretching them a lot and then lowering the field systematically. Eventually, I get to the point where the molecule stops stretching. Something I noticed, however, was that if the knots were big enough, the molecule would collapse sooner, at a higher tension than expected for a molecule without a knot. This suggested that the knot was modifying the coil-stretch transition.

To investigate this, my colleague Vivek Narsimhan, who is now a professor at Purdue, ran a series of computer simulations of knotted polymer chains. The simulations involve having a chain of connected beads that have short-range repulsive interactions between the beads that prevent them from passing through each other. Each bead is subject to Newton’s laws of motion, a drag force that depends on its velocity, as well as a random force that mimics thermal fluctuations (this is known as Brownian Dynamics, which is a subset of Langevin Dynamics, which is a subset of Molecular Dynamics). The initial conditions of the simulation are an extended chain with a knot in it, and we use different kinds of knots by copying their lattice coordinates from this site. Vivek simulated nine different types of knots at varying strengths of flow, starting with the chains highly stretched and letting them evolve to their steady-state configuration.

For the first part of the simulation, he simply measured how much the molecule was stretching under different conditions, varying the flow strength from very weak (below the stretch-coil transition) to very strong (the chain is stretched to almost 100% of its full length). Compared to a molecule with no knot, a knotted polymer will stretch less at a given tension, and this decreases as the knot gets bigger. This is not particularly surprising, if part of the chain is in a knot, that part can’t get stretched. However, the physics is a bit more complicated than just an effectively shorter chain not stretching as much: decreasing the length also decreases the internal relaxation time of the molecule, meaning a stronger flow rate is required to stretch it to the same degree. With corrections for the shorter maximum length and the faster internal relaxation, all the data collapsed onto one nice curve.

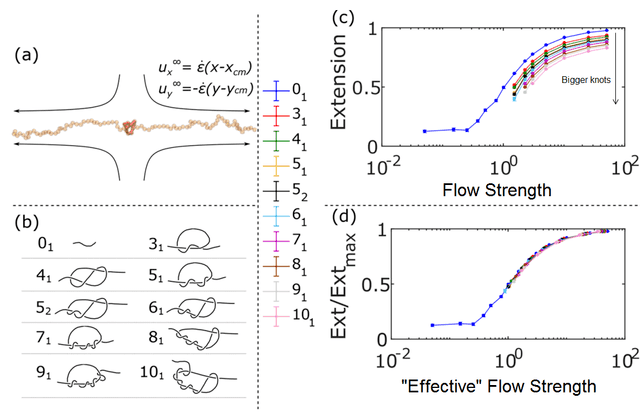
The basic simulation scheme and the roster of knots that were simulated. The top-right figure shows how much the molecule stretches as a function of the strain rate of the fluid (actually the Weissenberg number, which I haven’t gone into in this article). The bottom right shows how the data collapses if you correct for the effects of the knot.

What was more interesting was what happened just above the boundaries of the coil stretch transition. Whereas an unknotted chain would simply evolve to its steady-state level of stretch, the inflow of the same strength a knotted chain collapses into a coil: it is below the coil-stretch transition. However, eventually, it spontaneously stretches again, this time without a knot. In addition to predicting something interesting that happens to single polymers, it may also have implications for the flow of bulk polymer solutions, which may require higher-than-expected flow to prevent them from contracting. It was also something I had noticed in experiments, quite repeatably. When knots untie, the molecule temporarily contracts and then restretches after the untying is done.  It doesn’t always collapse, but it almost always contracts.

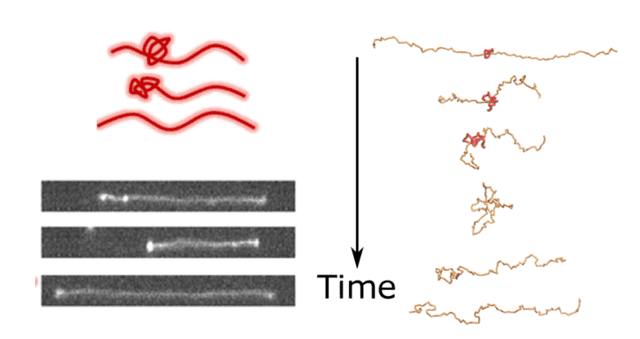
The untying-contraction process. When a knot reaches the end of the molecule, it forms a bulb and the molecule becomes less stretched. Then after it unties, the molecule re-stretches. The top left shows a cartoon, the bottom left shows an image sequence from the experiments, and the sequence on the right is from the simulations.

Another thing I had seen in experiments was that when knots untie, it doesn’t happen all at once. If a molecule starts with a big knot, it can get to the end, do its little contract-and-restretch dance, and still have a smaller knot remaining. This can repeat, and the second knot can untie, or leave an even smaller knot. The most stages I have seen this happen over is five. I compiled statistics and found that the knots untie in multiple stages about 60% of the time. The discovery of multi-stage untying caught me by surprise, I wasn’t expecting to see that and didn’t even think it was possible before I saw it happen.

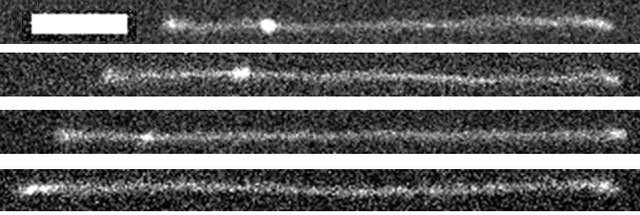
The same molecule at four stages of untying. Starts with a big knot, then it partially unties into a medium knot, then into a small knot, then into no knot. The scale bar is 8 microns, and each image is about one minute apart.

We looked for a point of comparison with the biggest knot used in simulations, the 10-crossing twist knot, which is what you get when you make a loop, twist it four times and then open the loop at one end and pass one strand through the other loop. If this knot is on an open string, it is asymmetric and can untie two ways. If the end of the string comes out of the loop, the whole thing unties, but if the other end of the string comes through the knot, it becomes an 8-crossing twist knot. That can do the same, untying or becoming a six-crossing knot, etc.

 

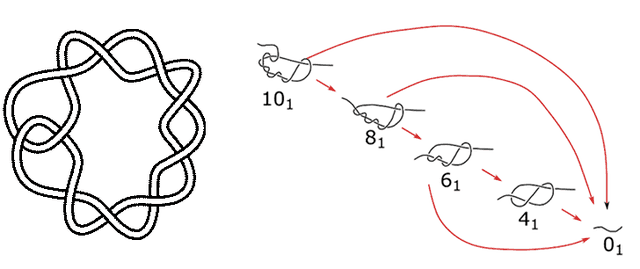
The ten-crossing, eight-half-twist knot (aka 10_1), and the ways it can untie.

Determining what kind of knot you have is non-trivial. There are several ways to do it, but the one that is used most often in polymer simulations involves calculating something called an Alexander Polynomial. This involves projecting the knot onto a plane and keeping track of which strands cross over others and which strands cross under. Then you can define a matrix based on a system of equations encapsulating information about the over/under-ness of the crossings, and then calculate its determinant, which gives you a polynomial (one with negative powers, usually). This was a vague description, you can read more here, e.g. on page 21.  If you calculate the polynomial at some value, you get a number that can be compared to known values from tabulated knots. There are some non-uniqueness issues with this (there’s an 8-crossing knot with the same Alexander polynomial as an unknot), but all the possibilities for a 10-crossing twist knot untying are unique, so by calculating it throughout the simulation, we can track how the type of knot evolves from big to small to unknotted. (I wish I could do this during experiments too).

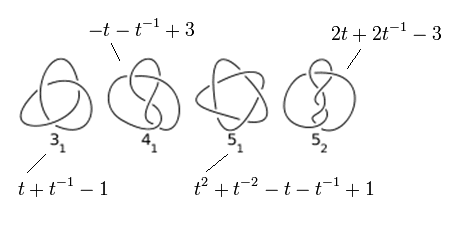
The Alexander polynomials of the four simplest knots.

The simulations also showed that knots were likely to be untied in different numbers of stages. Compared to experiments, the single-stage untying events were less common (which is somewhat unexpected, because I feel like if either end is likely to come out of the knot first, it should unravel completely 50% of the time). The agreement between theory and experiment here was pretty bad, but this wasn’t too much of an issue for a few reasons. One is that we can’t see the true number of unfolding steps, because the untying process is hidden below the resolution limit of the microscope and camera (both spatial and temporal). It is likely much larger than I can observe. The other is that the simulations are not a replica of the experimental conditions; the DNA molecules I use are significantly longer than the chains being simulated, the knots are more complicated, and there are other interactions that the simulations don’t take into account. I was happy with the computational vindication that knots can untie in stages, which as I mentioned caught me by surprise.

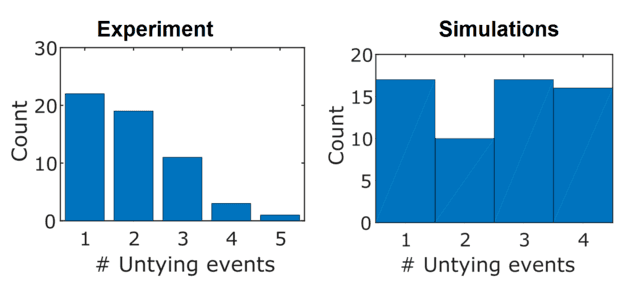
How many stages does it a knot take to untie? Not the best agreement between theory and experiment.

Conclusion

Overall, this paper was a nice convergence of simulation and experiment. On the simulation side, Vivek started looking at the general properties of knotted chains in extensional flow and then focused on the case of untying near the stretch-coil transition. On the experiment side, I noticed that the DNA molecules were shrinking as the knots untied and that they were doing these cool multi-stage unties. The simulations qualitatively replicated what I was seeing experimentally. These results may have some implications for the flow of bulk polymer solutions, but I just thought the phenomena we are investigating are cool.

* I wrote this description that may be illustrative, then decided to remove it from the main text: Imagine a square basin full of honey. In the middle of the East and West walls of the basin, there were two holes that the honey was draining out of. However, in the middle of the North and South walls, two faucets were flowing honey in at the same rate. A particle entrained in the honey coming from the North faucet would flow in with some initial velocity in the South direction, and that velocity would decrease as it approached the East-West axis, meanwhile gaining velocity in the East or West direction until it flows out at high velocity.

**I use an electric field that mimics extensional flow, not actual extensional flow.