How to Use the Spaghetti-Twist Method to Align DNA

A new paper from a collaboration of Canadian physicists has demonstrated how simply twirling a wire through a solution of DNA molecules can align the molecules around the wire, similar to the way that twirling a fork can align noodles around it. The paper was published in Physical Review X (PRX), an open-access journal that covers all areas of physics.

To understand what motivated a group of physicists to work on twirling DNA molecules, it is useful to consider that genomics and bioanalysis technologies rely on imaging fluorescent probes attached to DNA molecules. To visualize the genetic information stored in DNA, it is useful for different sections of the molecule to be arranged in space the same way that they are arranged along the genome, with one gene appearing in an image next to the gene that follows it in the genetic sequence. The laws of thermodynamics, unfortunately, work against this goal, as molecules tend to form a spatially disorganized “random coil”: there are many ways to arrange a long molecule randomly, but only one way when it is stretched, so entropy increases as the molecule contracts.  If you look at an image of a DNA molecule in solution or the cell, two genes that are very far apart along the molecule could appear very close in the image, and not much can be learned from looking at how the molecule is organized.

Key Points

1. Canadian physicists have developed a method to align DNA molecules by twirling a wire through a solution of DNA molecules.
2. This method was published in an open–access journal, Physical Review X (PRX).
3. Stretching DNA is necessary to visualize the genetic information stored in the molecule, but entropy works against this goal.
4. This new method works by rotating a wire with a narrow diameter through a droplet containing fluorescently stained DNA molecules.
5. The relationship between the rotating speed of the wire and the amount of stretching is complex and involves polymer dynamics and fluid mechanics.
6. Attaching one end of the molecule to the wire results in the molecule stretching around the wire several times, like a French horn.
7. The authors were limited by the length of the molecules they could work with and could not verify their theoretical predictions.
8. This method could potentially be used for bio–analysis.

Stretching DNA

Stretching DNA is thus both a useful problem and one that requires temporarily defeating entropy, which is why it interests biophysicists. Some solutions include stretching individual molecules with optical tweezers or confining molecules in very narrow tubes that force the molecule to stretch. The latter is now a commercially available technology for genetic mapping, but these approaches can be difficult to scale up towards genomic-length molecules. The authors of the PRX paper wanted to develop a method that could stretch arbitrarily long molecules with ease.

Perhaps inspired by twirling a fork through pasta during a meal at an Italian restaurant, the researchers surmised that a rotating liquid could stretch molecules through shear flow, a phenomenon that arises from gradients in the speed of a moving fluid. They set up a system where a wire with a narrow diameter (50 microns, similar to a human hair) was rotated on its axis through a droplet containing fluorescently stained DNA molecules, and imaged from below with a microscope. When the wire started rotating, it started to attract molecules toward it, and the molecules eventually stretched out and aligned around the wire. The authors found that the faster they rotated the wire, the more the DNA stretched, and with their maximum rotation rate of 130 rpm, the DNA stretched to about 30 times its equilibrium size.

A large portion of the paper is devoted to understanding the relevant physics that determine how a molecule will stretch around a rotating wire- a combination of polymer dynamics and fluid mechanics-and how to optimize the stretching. They found that when the rotation is slow, the stretching is simply proportional to the rotational frequency. When it is sped up, the relationship changes, to the point where increasing the rotation speed by a factor of sixteen would only double the extent of the stretching, which has implications for stretching very long molecules.

How can this be improved? Things get interesting of one end of the molecule is attached to the wire, such that it physically pulls the rest of the molecule around as it spins. The coupling between polymer physics and fluid mechanics implies that the tension is greatest and the molecule most stretched at the anchor point, and the tension decreases as you get farther away, leading to a molecule that gets more diffuse as you follow its spiraling contour. The authors liken this to a shofar, a musical instrument made from a sheep’s horn that is used in Jewish ceremonies, that gets wider and wider as the horn spirals. If the rotation is ramped even higher, the high-tension narrow part extends along the molecule, and if long enough it gets wrapped around the wire several times before flaring out at the end, like a French horn.

French horn twist

The authors attached a smaller DNA molecule t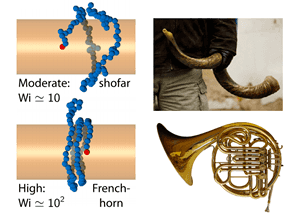o the wire (using a molecular dye that is notorious for sticking to things) and attempted to demonstrate that it was in the shofar configuration. However, one of the shortcomings of the paper, and the field of DNA polymer physics in general, is that they couldn’t work with molecules long enough to verify their theoretical predictions. The vast majority of papers in this field work with DNA comes from the genomes of two viruses that infect E. coli, one that is 48,000 base pairs and another that is 166,000 (the longer ones can be seen in the image above). The reason for this is that these are the two largest DNA molecules that money can buy, the shorter one being readily available in the US and the longer one having to be ordered from Japan. To get anything longer, it is necessary to “do biochemistry” or harvest them from cells, which is something physicists often aren’t equipped to do. Alas, it would have been interesting to see a very long molecule wrap around the wire multiple times as it spun.

Despite not being able to see the French horn twist, this was a fun paper to read, it’s a cool and elegant experiment and it could potentially lead to a new method of stretching DNA for bio-analysis. The synergy of pencil-and-paper theory, numerical simulations, and experiments worked well together and I hope to read more about this in the future.