Fibre Bundle: Definition, Examples & Intuitive Guide
Table of Contents
Definition / Summary
Fibre bundle — intuitively, a fibre bundle is a space E that locally looks like a product B × F but may have a different global topological structure. This article uses the British spelling “fibre”.
Extended explanation
Definition
A fibre bundle is the data (E, B, π, F), where E, B and F are topological spaces called the total space, the base space, and the fibre respectively, and π : E → B is a continuous surjection called the projection (or submersion) of the bundle. We will often assume the base space B is connected.
Local triviality
The local triviality condition requires that for every point x ∈ E there exists an open neighbourhood U of π(x) such that the preimage π−1(U) is homeomorphic to the product U × F. The homeomorphism is required to commute with the projection in the sense that π corresponds to the projection onto the first factor U.
Each such neighbourhood U is called a trivialization neighbourhood. A collection of pairs {Ui, φi} that cover the base is called a local trivialization, where φi : π−1(Ui) → Ui × F is a homeomorphism for each i.
Visualization
A useful, down-to-earth visual is the household hairbrush. Think of the handle as the base space B (a cylinder) and the bristles as the fibres F (short line segments). The projection π : E → B sends each point on a bristle to the point on the handle where that bristle is attached.
In the trivial bundle case, E is literally the product B × F and π is the coordinate projection onto the first factor. Such a bundle is called the trivial bundle.
Examples
Non-trivial examples include the Möbius strip and the Klein bottle. For example, the Möbius strip is locally homeomorphic to ℝ2 but globally has a twist that prevents it being the product S1 × I.
A smooth fibre bundle is defined similarly using smooth manifolds for B, F and E and requiring π and the local trivializations φi to be smooth maps.
Smooth bundles and structure groups
More generally, transitions between local trivializations are often required to lie in a topological (or Lie) group G called the structure group or gauge group, which acts on the fibre F. The transition functions then determine how the local product charts are glued together to form the global bundle.
Further reading
See also: The Pantheon of Derivatives (part 3).
Comments thread
This article was authored by several Physics Forums members with PhDs in physics or mathematics.

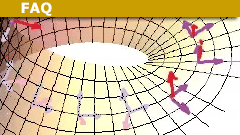





A nice experiment is to clue a strip from paper and cut it along the ring in the middle.
If you look at a small neighborhood of the Möbius strip, you will find a flat neighborhood with a one dimensional fiber at each point. This is the same as in the Euclidean plane with perpendicular one dimensional vector spaces attached at each point. However, if you consider the entire total space, then walking along a closed curve on the Möbius strip changes the direction (sign) of a vector in the fiber, whereas it does not on the Euclidean plane.
”
“see the first figure”
Where is it? I see no figure.
”
I have removed the language for now