Exploring a Paper on Scaling Laws and the Speed of Animals

Key Points

1. Scaling arguments are powerful tools in physics between vague descriptive arguments and rigorous formulae.
2. Examples of scaling arguments include the Square–Cube Law and Terminal Velocity.
3. A paper by Nicole Meyer–Vernet and Jean–Pierre Rospars examines the top speeds of organisms of varying sizes from bacteria to blue whales.
4.  The paper finds that the time it takes for an animal to move its body length is almost independent of mass across 21 orders of magnitude.
5. They derive a simple scaling argument and order–of–magnitude estimate for this remarkable fact.
6. Three features shared universally among moving organisms help explain this observation: density, force-per-unit area of muscle proteins, and metabolic rate per unit mass.
7. The authors argue that the maximum speed/body length is approximately 10 body lengths per second, depending on the zeroth power of mass.

Introduction

In a recent American Journal of Physics issue, I read an interesting paper by Nicole Meyer-Vernet and Jean-Pierre Rospars examining the top speeds of organisms of varying sizes, from bacteria to blue whales. They found that the time it takes for an animal to move its body length is almost independent of mass, across 21 orders of magnitude. They derived a simple scaling argument and order-of-magnitude estimate for this remarkable fact. Before further elaborating on their paper, I will give an overview of scaling arguments and their power.

Scaling Arguments

There is a false dichotomy in physics: concepts can either be explained in quasi-philosophical vague descriptive arguments or in terms of rigorous formulae that take years of study to understand. For example, one could describe general relativity with the bowling-ball-on-a-bedsheet analogy, and when that fails, crack out the Einstein field equations. However, this sad dichotomy is a happy trichotomy: in between the two extremes is the powerful tool of scaling arguments.

A scaling argument is a step above a Fermi calculation. In a Fermi calculation, we make approximations of various parameters in a formula and multiply them together to estimate an order of magnitude, neglecting precision. With a scaling argument, we examine how a dependent quantity changes as an independent quantity is varied, neglecting finer details, and dimensionless coefficients, and look only at the limiting behavior.

A well-known example is the Square-Cube Law, dating back to Galileo and described quite well in the Haldane essay, On Being the Right Size. The Square-Cube Law essentially states that if something, be it a chair or a person or whatever, was made twice as tall, twice as wide, and twice as deep, its volume and mass would increase by a factor of eight, but its ability to support that mass, its cross-sectional area, would only increase by a factor of four. This means as things get bigger, their weight becomes more significant compared to their strength (ants can carry 50 times their weight, squirrels can run up trees, and humans can do pull-ups).

Another example is terminal velocity: the drag force depends on the cross-sectional area, which (assuming a spherical cow) goes as the square of the radius (or the two-thirds power of mass), while the weight depends on the volume, proportional to the cube of the radius or the first power of mass. As Haldane graphically puts it

You can drop a mouse down a thousand-yard mine shaft; and, on arriving at the bottom, it gets a slight shock and walks away, provided that the ground is fairly soft. A rat is killed, a man is broken, a horse splashes.

Of course, theoretical physics is more than about description, it’s about prediction. So, before writing this article I decided to make a prediction based on the square-cube law: the cross-section of a human is proportional to the square of their height, or the two-thirds power of their weight. Thus, if we measure the peak strengths of the strongest humans at different weights, they should scale with the two-thirds power of weight. I make this prediction without knowing anything about biomechanics, metabolism, and training, just the fact that bigger guys tend to be stronger.

Looking up the record for the heaviest deadlift (picking a bar off the ground to hip level) for men of varying weights, we see that the records do follow the two-thirds scaling law from the smallest lifters up to about 220 pounds. Above that, it breaks down because the lifters generally get fatter without getting much more muscular. One can do a power-law fit this data, and I find that the best-fit power is .67 ± 0.05, consistent with my 2/3 prediction. This article is not about weightlifting; I was using this as an example to show that I can make an accurate prediction about a complex system (the human body) with a very simple scaling argument. Note that these arguments are useful for predicting the power of a relationship, but aren’t necessarily good for predicting the actual value.

The deadlift world record at different body weights, and the 2/3 power-law prediction. Note that these axes are logarithmic, which means that power functions appear as straight lines. Because the data and the prediction appear to have the same slope on log axes, it means they scale with the same power.

Now, back to the animal speed paper. The main observation that the paper is based on is summarized in its only figure. They look at how many times an animal can cover its length in a second. Using humans as an example, Usain Bolt can cover his height about six times in a second, while swimmer Florent Manaudou can cover his length roughly once per second. Their sampling ranges from bacteria at 10^-16 kg who move by swirling flagella, to whales at 10⁵ kg who move by undulating their bodies, covering 21 orders of magnitude in mass. They argue that the average length-traversal time is roughly independent of mass across all these orders until you get to the very large, although there is a significant deviation about this average. Nevertheless, even if you take the fastest bacteria and compare it to the slowest whale to try to shoot down their argument, you will have to explain a -0.06 power law instead of a 0.0 power law, so their message stands: to zeroth-order, body traversal speed is independent of mass.

Why this is the case on scaling grounds

They care about deriving this constant relationship and estimating its magnitude (body-lengths-per-second), not exactly but to within a factor of ten.

They argue that the moving speed is determined by three features shared universally among moving organisms. The first is that because all life forms are mostly water and more-or-less buoyant, they have roughly the density of water, 1 kg/L. The second is that all motility is caused by the contraction of muscle proteins that have a similar structure across all life forms. Based on the non-covalent binding energy of these proteins and their diameter, the force-per-unit area they can exert is roughly 20,000 N/m². Could a square-meter cross-section of muscle support two tons? I’m picturing an elephant leg and I can’t believe it. The final feature is the metabolic rate per unit mass, which is related to an organism’s ability to transfer heat across its surface. The paper states that this is 2 kilowatts per kilogram of muscle. The paper doesn’t explain where this comes from, citing controversy in the literature. All these quantities have variation from organism to organism, but together it is still much less than the 20 orders of magnitude of mass that are being considered.

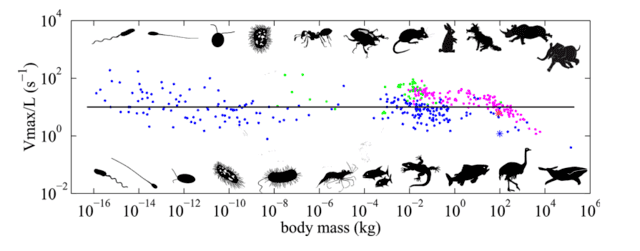
Top speed per length of organisms of various sizes. This image is from the paper I am discussing. If there is a copyright issue I can remove it.

The authors use dimensional analysis to figure out what powers of each quantity are required to describe the velocity per body length, which has units of frequency (meters per second per meter). They show that

Maximum speed/body length ~= (metabolic rate)x(density)/(protein fibre strength)~=10 body lengths per second

And this is a constant, depending on the zeroth power of mass, as was insinuated by the data. To reiterate, their standard of merit for this “prediction” isn’t that all animals cover their body length ten times per second, but that creatures of all sizes are roughly within an order of magnitude: a tenth to ten times this prediction. The paper goes on and gives some mechanical explanations as to why this makes sense; the energy required and work performed in wagging a flagella or moving a leg. The article also addresses the fact that there does seem to be a negative scaling between size and speed for the biggest organisms and makes an argument that the mass-independent scaling law applies to creatures up to 1.4 meters in size.

Conclusion

Overall, I enjoyed reading this paper because it took a fairly remarkable fact and explained it using the simple but powerful tools of scaling analysis and Fermi calculation. I thought it was cool how three features shared across all life forms lead to this universal locomotion frequency.

Click Here For the Forum Comments