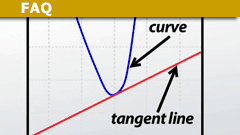
What is a Tangent Line? A 5 Minute Introduction

Definition/Summary

The tangent to a curve in a plane at a particular point has the same Gradient as the curve has at that point.

More generally, the (n-1)-dimensional tangent hyperplane to an (n-1)-dimensional surface in n-dimensional space at a particular point has the same Gradient as the surface has at that point.

So if $A\,=\,(a_1,a_2,\cdots a_n)$ is a point on a surface defined by the equation $F(x_1,x_2,\cdots x_n) = 0$, then the tangent hyperplane to the curve through $A$ is $\frac{\partial F}{\partial x_1}\arrowvert_A(x_1 – a_1)\,+\,\frac{\partial F}{\partial x_2}\arrowvert_A(x_2 – a_2)\,+\,\cdots\,\frac{\partial F}{\partial x_2}\arrowvert_A(x_n – a_n)\,=\,0$

If a curve in n dimensions is defined using a parameter t as $A(t)\,=\,(a_1(t),a_2(t),\cdots a_n(t))$ , then its tangent is:

$(x_1 – a_1) / \frac{da_1}{dt}\,=\,(x_2 – a_2) / \frac{da_2}{dt}\,=\,\cdots\,=\,(x_n – a_n) / \frac{da_n}{dt}$

Equations

For example, if the point $A\,=\,(x_0,y_0)$ lies on the circle:

$$F(x,y)\,=\,(x-p)^2+(y-q)^2\,-\,r^2\,=\,0$$ (1)

then $$\frac{\partial F}{\partial x}\arrowvert_A\,=\,2(x-p)\arrowvert_A\,=\,2(x_0-p)$$

and $$\frac{\partial F}{\partial y}\arrowvert_A\,=\,2(y-q)\arrowvert_A\,=\,2(y_0-q)$$

and so the equation of the tangent at $A$ is:

$$(x_0-p)(x-x_0)\,+\,(y_0-q)(y-y_0)=0$$ (2)

Alternatively, the same circle can be defined by $A(\theta)\,=\,(p+r\cos\theta, q+r\sin\theta)$

and so the equation of the tangent at $A(\theta)$ is:

$$\frac{x-p-r\cos\theta}{-r\sin\theta}\,=\,\frac{y-q-r\sin\theta}{r\cos\theta}$$

Extended explanation

We will transform the equation (2) into more convenient type for better way of memorizing and using the formula. Because of $M(x_1,y_1) /in K$:

$$(x_1-p)+(y_1-q)^2=r^2$$ (3)

If we sum the equations (2) and (3), we get:

$$(x_1-p)(x-x_1)+(y_1-q)(y-y_1)+(x_1-p)+(y_1-q)^2=r^2$$

$$(x_1-p)[x-x_1+x_1-p]+(y_1-q)[y-y_1+y_1-q]=r^2$$

$$(x_1-p)(x-p)+(y_1-q)(y-q)=r^2$$ (4)

The equation (4) is equation of tangent of the circle in the point $M(x_1,y_1) \in K$.

If the K have center (0,0), i.e $K: x^2+y^2=r^2$, then p=q=0, so the equation of the tangent is:

$$x_1x+y_1y=r^2$$

Extra

See also https://www.physicsforums.com/insights/the-pantheon-of-derivatives-i/ and the list at the beginning in https://www.physicsforums.com/insights/journey-manifold-su2mathbbc-part/ where I have listed a couple of different views of how a derivative can be seen. The slope wasn’t even among it!

Comment Thread