Why Do People Say That 1 And .999 Are Equal?
Why do people say 1 and 0.999… are equal? Aren’t they two different numbers?
No, they really are the same number, though this is often very counterintuitive to many beginning students. Here are some non-rigorous proofs that 1=0.999…:
Proof #1
For any two unequal numbers, there is always another number in between them. (That is intuitively obvious, and can be pictured on a number line, which will be familiar to many people.) Therefore, if 0.999…. and 1 are different, there must be another number in between them. But there is no way to write a number that is greater that 0.999… and less than 1 in decimal notation.
Proof #2
First, we put
[tex]\ x = 0.999…[/tex]
Multiplying by 10 gives us
[tex]\ 10x = 9.999…[/tex]
But then
[tex]\ 10x-x = 9.999…-0.999…,[/tex]
thus
[tex]\ 9x = 9[/tex]
Hence we get that
[tex]\ x = 1[/tex]
Proof #3
If you accept that 0.9999… is a number, then how much less than 1 is it? It’s larger that 0.9999, so it’s less than 0.0001 less than 1. But it’s also larger that 0.9999999, so it’s less than 0.0000001 less than 1. So the difference between 0.9999… and 1 is less than 0.00001, 0.000000001, or 0.any number of 0s followed by 1 … so the difference must be zero. If you accept that two numbers whose difference is 0 must be the same, then that proves that 0.9999… = 1. If you don’t accept that, and you think that two different numbers can have a difference of zero, then you’re in an ‘extended number system’ which has more numbers than we normally use.
Proof #4
First, we have that
[tex]\ 1/3 = 0.333…[/tex]
If we multiply things by 3, then we get
[tex]\ 1=3\times (1/3) = 3\times (0.333…) = 0.999…[/tex]
All of these proofs are correct, but they are not rigorous. For example, how do we know that [itex]3 \times (0.333…) = 0.999…[/itex]? This is not that obvious if we think about it. A more rigorous proof is given in the post following this one.
Some further questions you might have:
But 1 cannot equal 0.999…, as every number can only have one representation!
Well, the thing is that this is just a misconception that is simply not true. Numbers can have many representations. For example,
[tex]\frac{1}{3}=\frac{2}{6}=\frac{3}{9}=0.333… ,[/tex]
but somehow, many people don’t have any problems with this thing. The same thing happens to 1=0.999… really, it’s just another way to write the same number. Does this make our number system ugly? I understand that you might think that, but that’s just something we need to accept. Not having that 1=0.999… would make our number system much uglier!
The way I see it, is that 0.999… gets closer and closer to 1, but never quite reaches 1.
This reasoning appears a lot and apparently, many people see 0.999… as some kind of process that gets close to 1. But this is not quite what mathematicians mean with 0.999…
Mathematicians say that 0.999… is a number, just like 2 and 3. So phrases like “it gets close to 1, but never reaches 1” are meaningless. It’s the same as saying 1 gets closer and closer to 2, but never quite reaches 2. This sentence makes no sense, and the same thing happens with 0.999…
Can we define number systems such that 1=0.999… does not hold?
Of course! But these number systems are not as useful, because they don’t conform to our intuition about numbers and limits.
In Proof #2, you say 10x=9.999… But this 9.999… has one fewer nine than 0.999…
Another popular argument. This time, the confusion arises from not grasping infinity. 0.999… has an infinite number of nines. If we somehow remove a nine from this sequence, then we would still have an infinite number of nines. So there are an equal number of nines in 0.999… and 9.999…
The same thing happens here: consider two sets of numbers, A and B, where
[tex]A=\{0,1,2,3,4,…\}[/tex]
and
[tex]B=\{1,2,3,4,…\}[/tex]
Both sets are infinite. And actually, both sets have an equal number of elements. But A doesn’t contain 0, so it has one fewer element than B? Yes, but this reasoning only applies to finite sets. For infinite sets, it’s quite possible to have one element less and still have an equal number of elements. Indeed, consider the following correspondence:
[tex]0\leftrightarrow 1,~1\leftrightarrow 2,~2\leftrightarrow 3,~3\leftrightarrow 4,…,~n\leftrightarrow n+1,…[/tex]
So for an element n in A, there exists a unique element in B that corresponds to n, namely n+1. This means, by definition actually, that both sets have the same number of elements.
Read this supportive article: https://www.physicsforums.com/insights/is-there-a-rigorous-proof-of-1-0-999/
Maybe we should just abandon our base 10 number system and move to a number system where every number does have a unique representation.
Tempting, but sadly this is not possible. The problem arises in every base! For example, in base 2, we have [itex]1=0.111…[/itex]. There is no way around it.
The following forum members have contributed to this FAQ:
AlephZero
Fredrik
micromass
tiny-tim
vela
This article was authored by several Physics Forums members with PhDs in physics or mathematics.





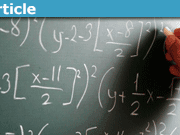

[QUOTE=”Kegan, post: 5383121, member: 584906″]And who is Gauss[/QUOTE]
[URL]https://en.wikipedia.org/wiki/Carl_Friedrich_Gauss[/URL]
Maybe the best Mathematician of all times. Hope he is not pissed I am using his name. I assume you are young , since you’re interested in Math and don’t know about Gauss. Maybe between 10 and 20.
[QUOTE=”Kegan, post: 5383118, member: 584906″]oh ok and i have a question for you how old do you think i am ,seriously[/QUOTE]
And who is Gauss
[QUOTE=”WWGD, post: 5383115, member: 69719″]Close: What Would Gauss Do.[/QUOTE]
oh ok and i have a question for you how old do you think i am ,seriously
[QUOTE=”Kegan, post: 5383114, member: 584906″]and i really like your username does it stand for” what would god do”[/QUOTE]
Close: What Would Gauss Do.
[QUOTE=”Kegan, post: 5383112, member: 584906″]yeah I Know i just forgot the….[/QUOTE]
and i really like your username does it stand for” what would god do”
[QUOTE=”WWGD, post: 5375555, member: 69719″][USER=584906]@Kegan[/USER] It is not .999 , it is .9999….. with an infinite string of 9s.[/QUOTE]
yeah I Know i just forgot the….
[QUOTE=”Isaac0427, post: 5375627, member: 552304″]Instead of thinking of .999… as a number, think of it as the limit of the sequence (.9,.99,.999,.9999,…) as n approaches infinity. That is what the 3 dots mean. The limit of that sequence as n approaches infinity is 1.
Here’s another example: (1/0!)+(1/1!)+(1/2!)…=e, however if you stop the sequence at any value of n, the answer will not be e. Does this make sense?[/QUOTE]
yeah that does make more sense so what you saying is that .999… to infinity approaches the number 1 so close it is consideribly the same number is that what you are saying ?
[QUOTE=”MrAnchovy, post: 5375864, member: 385977″]To be fair, Isaac didn’t say it was not a number. He just suggested that it might be easier to see that 0.9999… is the limit of the sequence 0.9, 0.99, 0.999, …, and that the limit of that sequence is also equal to 1, than it is to make the jump from the recurring decimal to 1 directly.[/QUOTE]
That was the point. I understand it is a number, but the value of the number can be thought of the limit of that sequence. IMO, this is easier to comprehend, but as you said, it’s a mater of opinion.
[QUOTE=”WWGD, post: 5375896, member: 69719″]Yes, maybe it is not the best example, but the point I wanted to make is that two things don’t need to be strictly equal in order to be considered the same. It is more a ” to the effects of what we are doing, these two expressions are equal” EDIT: Maybe non-trivial, i.e., non-identity isomorphisms would be a better example.[/QUOTE]
I was going to write that one could consider the distinction between numerals or formulas on the one hand and numbers on the other. It seems that the distinction you want to make is between exemplars of an equivalence class and the class itself.
6 of one, ##frac{dozen}{2}## of the other.
[QUOTE=”MrAnchovy, post: 5375887, member: 385977″]I don’t think days of the week, which are analogous to integers mod 7 is a helpful analogy to the reals. And 2/2 is an expression which is equal to 1, it is not a valid representation of a rational number: the numerator and denominator must have no common factor.[/QUOTE]
Yes, maybe it is not the best example, but the point I wanted to make is that two things don’t need to be strictly equal in order to be considered the same. It is more a ” to the effects of what we are doing, these two expressions are equal” EDIT: Maybe non-trivial, i.e., non-identity isomorphisms would be a better example.
[QUOTE=”MrAnchovy, post: 5375887, member: 385977″]I don’t think days of the week, which are analogous to integers mod 7 is a helpful analogy to the reals. And 2/2 is an expression which is equal to 1, it is not a valid representation of a rational number: the numerator and denominator must have no common factor.[/QUOTE]
2/2 is a perfect representation of a rational number.
I don’t think days of the week, which are analogous to integers mod 7 is a helpful analogy to the reals. Edit: the rest of this is rubbish [s]And 2/2 is an expression which is equal to 1, it is not a valid representation of a rational number: the numerator and denominator must have no common factor.[/s]
The confusion seems largely to stem from the implicit assumption that a number can have only one representation. Instead, a number is an equivalence class; one sees this in daily life, e.g., today is Friday, and (ignoring modular issues) any date 7k days from now is also a Friday, so if the difference between the dates (again, re modularity) is a multiple of 7 , then both are the same day of the week. And then there is 2/2, 3/3 , etc.
[QUOTE=”micromass, post: 5375840, member: 205308″]No. 0.99999…. [B]is[/B] a number.[/QUOTE]
To be fair, Isaac didn’t say it was not a number. He just suggested that it might be easier to see that 0.9999… is the limit of the sequence 0.9, 0.99, 0.999, …, and that the limit of that sequence is also equal to 1, than it is to make the jump from the recurring decimal to 1 directly.
This illustration is not IMHO any less rigorous than the 9.9999… – 0.9999… illustration of the identical equality to 1. Whether it is easier to comprehend or not is a matter of personal taste.
[QUOTE=”Isaac0427, post: 5375627, member: 552304″]Instead of thinking of .999… as a number[/QUOTE]
No. 0.99999…. [B]is[/B] a number.
[QUOTE=”Kegan, post: 5375551, member: 584906″]i’m 11 i understand that 1 and .999 are two completely different numbers and in math you don’t round numbers to get precise answers it just doesn’t work like that[/QUOTE]
Instead of thinking of .999… as a number, think of it as the limit of the sequence (.9,.99,.999,.9999,…) as n approaches infinity. That is what the 3 dots mean. The limit of that sequence as n approaches infinity is 1.
Here’s another example: (1/0!)+(1/1!)+(1/2!)…=e, however if you stop the sequence at any value of n, the answer will not be e. Does this make sense?
[QUOTE=”Kegan, post: 5375551, member: 584906″]i’m 11 i understand that 1 and .999 are two completely different numbers and in math you don’t round numbers to get precise answers it just doesn’t work like that[/QUOTE]
[USER=584906]@Kegan[/USER] It is not .999 , it is .9999….. with an infinite string of 9s.
The easiest proof for me is that:
0.9999999…=0.3333333…*3
0.3333333…=1/3
0.9999999…=(1/3)*3=1
Then 0.9999999…=1
Look that also, 0.999999…8=0.99999999(=1):
1.999999999…8=0.6666666666…*3
0.66666666…=2/3
1.999999…8=(2/3)*3=2=1+1=1+0.9999999…=1.999999…
Then 1.999999…8=1.999999999…
1.999999…8 -1= 1.99999… -1
So 0.999999…8=0.999999(=1…)
[QUOTE=”gmax137, post: 5322058, member: 112505″]Going back to post #2
Maybe (probably) I’m being dense, but didn’t you just add [itex]ar^n[/itex] to the left and [itex]ar^{n+ 1}[/itex] to the right?[/QUOTE]
Yes, that was a typo. It should have been [itex]ar^{n+1}[/itex] on both sides.
[QUOTE=”Isaac0427, post: 5315847, member: 552304″]Ok, I just talked to my math teacher. She explained it to me in person which helped. Thanks guys it really does help. I mostly understand it now, that as something gets so close to 1, for all practical purposes, it is equal to 1.[/QUOTE]
You can prove that there is no difference at all because the 9’s go forever. This proof may be your first encounter with a mathematical “proof by contradiction”. Suppose you assume that there is any difference between .999999… and 1. Say it is over 0.00001 (a formal mathematical proof would use an arbitrarily small ε > 0). Now use enough 9’s (0.999999999999) to show that there is less difference than that and that the difference will only decrease as you add more 9’s. That contradicts to your original assumption that the difference is greater than 0.00001 (or ε>0). It doesn’t matter how small your assumed difference is; you can add enough 9’s to get closer to 1 and contradict that assumption. So it proves that there can be no difference between 0.99999… and 1.
Going back to post #2
[QUOTE=”HallsofIvy, post: 5260930, member: 331″]
…
Restore that by adding [itex]ar^{n+1}[/itex] to both sides:
[itex]S_n- a+ ar^n= r(a+ ar+ cdotcdotcdot+ ar^{n-1})+ ar^{n+ 1}[/itex]
…[/QUOTE]
Maybe (probably) I’m being dense, but didn’t you just add [itex]ar^n[/itex] to the left and [itex]ar^{n+ 1}[/itex] to the right?
[QUOTE=”Isaac0427, post: 5315927, member: 552304″]I know what a limit is. She explained how for practical purposes [B]the limit .999… approaches 1[/B] is considered .999… being equal to one.[/QUOTE]
The part where I bolded indicates you [I]don’t[/I] know what a limit is. Limits don’t move and they don’t “approach”.
[QUOTE=”Isaac0427, post: 5315927, member: 552304″]I know what a limit is. She explained how for practical purposes the limit .999… approaches 1 is considered .999… being equal to one.[/QUOTE]
It is not “for practical purposes”. It is exact. The limit of the sequence .9, .99, .999, … does not approach 1. Successive terms in the sequence approach 1. The limit [B][I]is [/I][/B]1. The notation .999… denotes the limit. Hence .999…[I] [B]is[/B][/I] 1.
[QUOTE=”lavinia, post: 5315850, member: 243745″]Ask your math teacher to explain to you what a limit is.[/QUOTE]
I know what a limit is. She explained how for practical purposes the limit .999… approaches 1 is considered .999… being equal to one.
[QUOTE=”Isaac0427, post: 5315847, member: 552304″]Ok, I just talked to my math teacher. She explained it to me in person which helped. Thanks guys it really does help. I mostly understand it now, that as something gets so close to 1, for all practical purposes, it is equal to 1.[/QUOTE]
Ask your math teacher to explain to you what a limit is.
Ok, I just talked to my math teacher. She explained it to me in person which helped. Thanks guys it really does help. I mostly understand it now, that as something gets so close to 1, for all practical purposes, it is equal to 1.
[QUOTE=”Isaac0427, post: 5315835, member: 552304″]I thought it represented an infinitely small change of x. I could be wrong, however.[/QUOTE]
In the non-standard analysis, dx can be given meaning as an infinitesimal. In standard analysis, the dx in an integral is pure notation.
[QUOTE=”Isaac0427, post: 5315831, member: 552304″]dx is also infinitesimally small, but if it equaled zero, then any integral or derivative would equal zero or be undefined.[/QUOTE]
Remember I said in previous posts that the length of the rectangles in a fixed Riemann sum is bounded below. You then consider what happens as this approaches 0 in the limit, but this, dealing with limits, is a separate issue.
[QUOTE=”jbriggs444, post: 5315834, member: 422467″]dx is not a number. It is a notation.[/QUOTE]
I thought it represented an infinitely small change of x. I could be wrong, however.
[QUOTE=”Isaac0427, post: 5315831, member: 552304″]dx is also infinitesimally small, but if it equaled zero, then any integral or derivative would equal zero or be undefined.[/QUOTE]
dx is not a number. It is a notation.
[QUOTE=”WWGD, post: 5315605, member: 69719″]1-0.99999…. _is_ indefinitely small, so must equal zero.[/QUOTE]
dx is also infinitesimally small, but if it equaled zero, then any integral or derivative would equal zero or be undefined.
Yet another reason, maybe mentioned is that, by the Archimedean property, a Standard Real number cannot be indefinitely small; it must then equal zero. But the difference
1-0.99999…. _is_ indefinitely small, so must equal zero. So the two numbers are then equal.
[QUOTE=”Isaac0427, post: 5315347, member: 552304″]I know this discussion came off of my mentioning a Riemann sum. I meant a Riemann integral. My point was that in a Riemann integral, you add up an infinite amount of rectangles with a width of dx. dx, for the integral to have a nonzero value, couldn’t be zero, but it is, by definition, less than .00000000001, .00000000000000000000000001, or any number of zeros you put before the one. You would need an infinite amount of zeros. So, I know it may not be the proper notation, but the width of the rectangles would essentially be .000…1. If the fact that it gets infinitely close to zero makes it equal to zero, then a Riemann integral would have a value of zero, which is not the case. If we were to take some [U]fundamental[/U] length (in a coordinate system that has one), and have two particles of that size touch with a distance between them of zero, would they be in the same position? I say a fundamental size because the particle’s centers would have no distance between them.[/QUOTE]
This is not what the Riemann integral is. One does not add up an infinite number of rectangles of zero width.
The way I learned it, the Riemann integral is defined in terms of lower and upper sums. For a positive function, one divides a closed interval into finitely many closed segments then takes the length of each segment and multiplies it by the max or the min of the function in the segment. and adds the values up. These give you what are called lower and upper sums. [U]As WWGD said,[/U] [U]these segments have finite length and there are always only finitely many terms in the sum [/U]The Riemann integral is then the Least Upper Bound of all lower sums obtained by dividing the interval into finitely many segments of finite length. It is also the Greatest Lower Bound of all upper sums. A particular sum can be chosen to have segments of arbitrarily small length, but each sum always has finitely many segments and these segments always have finite length.
This same point is true for the expression ##.999…##
The three dots mean that number which is the Least Upper Bound of all finite decimal numbers, .9, .99, 999, .9999 etcetera. [U]It does not stand for some non-standard number in some other number system. [/U]It stands for that ordinary real number that is the LUB of the set of decimals ##{ .9,.99,.999, .9999}## etc
The number one is the least Upper Bound of all of these numbers. The proof shows that one can always find a finite decimal sequence of 9’s that is arbitrarily close to 1, Another way of saying this is that 1 is the limit of the sequence, ##x_1 = .9##, ##x_2 = .99 ##, … ## x_n = .999999## (n times)
[U]Hallsofivy gives a nice proof of this limit in Post #2[B].
[/B][/U]
Every positive number has a decimal expansion. For almost all of them, the decimal expansion is infinitely long. This means that almost every number is the Least Upper Bound of an infinite sequence of increasing decimal numbers. 1 is not special in any way.
I know this discussion came off of my mentioning a Riemann sum. I meant a Riemann integral. My point was that in a Riemann integral, you add up an infinite amount of rectangles with a width of dx. dx, for the integral to have a nonzero value, couldn’t be zero, but it is, by definition, less than .00000000001, .00000000000000000000000001, or any number of zeros you put before the one. You would need an infinite amount of zeros. So, I know it may not be the proper notation, but the width of the rectangles would essentially be .000…1. If the fact that it gets infinitely close to zero makes it equal to zero, then a Riemann integral would have a value of zero, which is not the case. If we were to take some [U]fundamental[/U] length (in a coordinate system that has one), and have two particles of that size touch with a distance between them of zero, would they be in the same position? I say a fundamental size because the particle’s centers would have no distance between them.
[QUOTE=”WWGD, post: 5315064, member: 69719″]The maximal width goes to 0 if we consider a net of Riemann sums. In order to compute the Riemann integral, we consider what happens as the width of partitions go to zero.
But any sum has a minimal width.
[/quote]Yes, I understand all of this.
What I disagree with, and keep carping on, your assertion that the widths of the rectangles can be “going to 0” and at the same time “these widths do not become indefinitely-close to 0”. Obviously, both of these can’t be true.
[QUOTE=”Mark44, post: 5315054, member: 147785″]Please explain to me how the widths of the rectangles can be “going to 0” and at the same time “these widths do not become indefinitely-close to 0” — your words.
I maintain that you can’t possibly be talking about a specific Riemann sum with a specific number of terms (hence a specific number of rectangles, all of whose areas are positive numbers).[/QUOTE]
The maximal width goes to 0 if we consider a net of Riemann sums. In order to compute the Riemann integral, we consider what happens as the width of partitions go to zero.
But any sum has a minimal width.
I don’t mean to be disrespectful, but this conversation does not seem to be going anywhere productive and frankly, I would like to leave it at this. I am not blaming it on you, but we either drop it or take a different tack to it, because otherwise we will be going ( at least seemingly) in circles for a long time here. We are just not communicating effectively here; I suggest we leave it at this, at least for now. No disrespect intended.
[QUOTE=”Mark44, post: 5314659, member: 147785″]We are not talking about a specific Riemann sum. My complaint is that you are talking about a limit, but don’t seem to realize it. Emphasis added.
In other words, as ##Delta x to 0## — that’s a limit. All the other stuff about compact sets, continuity, and subcovers etc. is just word salad that I’m 99% sure would be over the head of the person you were responding to.[/QUOTE]
I think that WWGD is trying to point out that on an open interval one would need to divide it into an infinite sequence of closed intervals whose lengths would become arbitrarily small near the edge of the interval. On a closed interval one can choose a subdivision that is finite.
[QUOTE=”WWGD, post: 5315049, member: 69719″]No, I am definitely talking about an individual Riemann sum. By a controlled way, I mean there is a lower bound for the widths, which there is by the usual arguments. I think the confusion here is you are referring to the Riemann integral, while I am referring to specific Riemann sums.[/QUOTE]
Please explain to me how the widths of the rectangles can be “going to 0” and at the same time “these widths do not become indefinitely-close to 0” — your words.
I maintain that you can’t possibly be talking about a specific Riemann sum with a specific number of terms (hence a specific number of rectangles, all of whose areas are positive numbers).
[QUOTE=”Mark44, post: 5315045, member: 147785″]When you say, “the rectangles, [B]while going to 0, …[/B]” you’re no longer talking about a specific Riemann sum — you’re talking about the limit of the Riemann sums (as the number of terms goes to infinity), which means you’re talking about the Riemann [U]integral[/U].
These were your exact words:
In short, you’re saying that the rectangles are going to zero and that their widths are not going to zero. That’s impossible.
Also, I don’t know what you mean “goes to zero in an uncontrolled way” …[/QUOTE]
No, I am definitely talking about an individual Riemann sum. By a controlled way, I mean there is a lower bound for the widths, which there is by the usual arguments. I think the confusion here is you are referring to the Riemann integral, while I am referring to specific Riemann sums.
[QUOTE=”WWGD, post: 5315036, member: 69719″] I was referring to individual Riemann sums, not to the Riemann integral itself. I was addressing the question of whether a Riemann sum is zero or not, because the general term goes to zero in an uncontrolled way.[/quote]
When you say, “the rectangles, [B]while going to 0, …[/B]”[B] [/B]you’re no longer talking about a specific Riemann sum — you’re talking about the limit of the Riemann sums (as the number of terms goes to infinity), which means you’re talking about the Riemann [U]integral[/U].
These were your exact words:
[quote]I think the point is that the rectangles, [B]while going to 0[/B], are uniformly bounded , by compactness of the region of integration, so these widths do not become indefinitely-close to 0[/quote]In short, you’re saying that the rectangles are going to zero and that their widths are not going to zero. That’s impossible.
Also, I don’t know what you mean “goes to zero in an uncontrolled way” …
[QUOTE=WWGD] I made no reference to the Riemann integral itself; that is a whole other topic. But yes, the Riemann integral is the limit as the partition width goes to zero. I don’t see why the two contradict or are incompatible with each other.[/QUOTE]
[QUOTE=”Mark44, post: 5315034, member: 147785″]I think you mean Riemann [U]integral[/U] being the limit of the Riemann sums.
My complaint is in the following. I interpret the phrase “while going to 0” as equivalent to saying “the limit of the Riemann sums as n goes to infinity.” You can’t say that the widths of the rectangles are going to zero, but at the same time do not become close to zero. Here again is what you said, with emphasis added.
The rectangle widths are either going to zero or they’re not — you can’t have it both ways.[/QUOTE]
Yes, I meant Riemann integral, my bad. I was referring to individual Riemann sums, not to the Riemann integral itself. I was addressing the question of whether a Riemann sum is zero or not, because the general term goes to zero in an uncontrolled way. I made no reference to the Riemann integral itself; that is a whole other topic. But yes, the Riemann integral is the limit as the partition width goes to zero. I don’t see why the two contradict or are incompatible with each other.
[QUOTE=”WWGD, post: 5314986, member: 69719″]No, I think you are not realizing my point. I am talking about an individua Riemann sum not being 0, addressing the question. I do know that the Riemann sum is the limit ( if it exists) of the Riemann sums.
[/quote]I think you mean Riemann [U]integral[/U] being the limit of the Riemann sums.
[QUOTE=WWGD] I never said nor implied otherwise. I did reply to the OP that for individual sums, the width is controlled, so it does not go to zero. The rest of the exchanges were with and for you.[/QUOTE]
My complaint is in the following. I interpret the phrase “while going to 0” as equivalent to saying “the limit of the Riemann sums as n goes to infinity.” You can’t say that the widths of the rectangles are going to zero, but at the same time do not become close to zero. Here again is what you said, with emphasis added.
[quote=WWGD]I think the point is that the rectangles, [B]while going to 0[/B], are uniformly bounded , by compactness of the region of integration, so these widths do not become indefinitely-close to 0[/quote]
The rectangle widths are either going to zero or they’re not — you can’t have it both ways.
[QUOTE=”Mark44, post: 5314659, member: 147785″]We are not talking about a specific Riemann sum. My complaint is that you are talking about a limit, but don’t seem to realize it. Emphasis added.
In other words, as ##Delta x to 0## — that’s a limit. All the other stuff about compact sets, continuity, and subcovers etc. is just word salad that I’m 99% sure would be over the head of the person you were responding to.[/QUOTE]
No, I think you are not realizing my point. I am talking about an individua Riemann sum not being 0, addressing the question. I do know that the Riemann sum is the limit ( if it exists) of the Riemann sums. I never said nor implied otherwise. I did reply to the OP that for individual sums, the width is controlled, so it does not go to zero. The rest of the exchanges were with and for you.
[QUOTE=”jbriggs444, post: 5314942, member: 422467″]The phrasing that madness used was careful and avoided speaking of the result of a never-ending process.[/QUOTE]
Fair enough. It’s not the way I read it, but my apologies to madness.
[QUOTE=”PeroK, post: 5314918, member: 493650″]Perhaps, but my original point was that there are those who see the limit as a number (full stop) and those who see the limit as the hypothetical result of a never-ending process. Breaking away from this latter view is perhaps an important step in grasping rigorous maths.[/QUOTE]
The phrasing that madness used was careful and avoided speaking of the result of a never-ending process.
[QUOTE=”madness, post: 5314878, member: 28629″]Yes, but it’s also important to remember that this number (the limit) is the number that you get closer and closer to as you apply the process of increasing n. Or, if you don’t like this process, it’s the number that you can get as close to as you like by choosing a high enough value of n.[/QUOTE]
[QUOTE=”HallsofIvy, post: 5314902, member: 331″]Neither is a rigorous definition of a limit but they are a statement of what is implied by such a definition. In particular, the [B]limit[/B] of the sequence 0.9, 0.99, 0.999, … is the [B]number[/B] 1, not the sequence itself.[/QUOTE]
Perhaps, but my original point was that there are those who see the limit as a number (full stop) and those who see the limit as the hypothetical result of a never-ending process. Breaking away from this latter view is perhaps an important step in grasping rigorous maths.
[QUOTE=”PeroK, post: 5314897, member: 493650″]Neither of those is the definition of a limit.[/QUOTE]
Neither is a rigorous definition of a limit but they are a statement of what is implied by such a definition. In particular, the [b]limit[/b] of the sequence 0.9, 0.99, 0.999, … is the [b]number[/b] 1, not the sequence itself.
[QUOTE=”PeroK, post: 5314897, member: 493650″]Neither of those is the definition of a limit.[/QUOTE]
Actually, the second one is.
[QUOTE=”madness, post: 5314878, member: 28629″]Yes, but it’s also important to remember that this number (the limit) is the number that you get closer and closer to as you apply the process of increasing n. Or, if you don’t like this process, it’s the number that you can get as close to as you like by choosing a high enough value of n.[/QUOTE]
Neither of those is the definition of a limit.
[QUOTE=”PeroK, post: 5314803, member: 493650″]It is important, though, to realise that a limit is a number, and not a process. It’s a small point, perhaps, but it sharpens your understanding of these things.[/QUOTE]
Yes, but it’s also important to remember that this number (the limit) is the number that you get closer and closer to as you apply the process of increasing n. Or, if you don’t like this process, it’s the number that you can get as close to as you like by choosing a high enough value of n.