Boundary Definition and 900 Threads
-
T
Graduate Definition of the boundary map for chain complexes
I've been poking around, learning a little about homology theory. I had a question about the boundary operator. Namely, how it's defined. There's two definitions I've seen floating around. The first is at: http://en.wikipedia.org/wiki/Simplicial_homology The second, at...- Tac-Tics
- Thread
- Boundary Chain Definition Map
- Replies: 4
- Forum: Differential Geometry
-
M
Graduate Criteria of periodic boundary condition
We used to apply periodic boundary condition to simulate an infinite system. What will happen if the interactions between atoms do not drop to zero even when they are infinitely far away? Is the periodic boundary still valid? How can I prove the periodic boundary condition is valid or not? thanks.- mmssm
- Thread
- Boundary Boundary condition Condition Criteria Periodic
- Replies: 1
- Forum: Atomic and Condensed Matter
-
G
Graduate Condition of continuity of E field at a boundary
I am trying to understand the derivation of Snell's law using Maxwell's equation and got stuck. My textbook says that "the E field that is tangent to the interface must be continuous" in order to consider refraction of light. If it were static E field I understand this is true because in...- Gen1111
- Thread
- Boundary Condition Continuity Field
- Replies: 6
- Forum: Electromagnetism
-
J
PDE with variable boundary condition
Homework Statement I am trying to solve this PDE with variable boundary condition, and I want to use combination method. But I have problem with the second boundary condition, which is not transformed to the new variable. Can you please give me some advise? Homework Equations (∂^2 T)/(∂x^2...- jafanasim
- Thread
- Boundary Boundary condition Condition Pde Variable
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
S
Graduate Laplace equation in a square with mixed boundary conditions
The length of the side of the square is a. The boundary conditions are the following: (1) the left edge is kept at temperature T=C2 (2) the bottom edge is kept at temperature T=C1 (3) the top and right edges are perfectly insulated, that is \dfrac{\partial T}{\partial x}=0,\dfrac{\partial...- samuelandjw
- Thread
- Boundary Boundary conditions Conditions Laplace Laplace equation Mixed Square
- Replies: 13
- Forum: Differential Equations
-

Graduate In holographic principle, the boundary is wrt which light cone?
It is stated that in the holographic principle (e.g., in http://en.wikipedia.org/wiki/Holographic_principle) that the the description of a volume of space is encoded on a light-like boundary to the region. But with respect to which position in the volume? In a black hole, it is clear, because...- nomadreid
- Thread
- Boundary Cone Holographic Holographic principle Light Light cone Principle
- Replies: 1
- Forum: Beyond the Standard Models
-
C
2-D Poisson Equation Boundary Value Prob
Homework Statement Solve the equation: ∂2F/∂x2 + ∂2F/∂y2 = f(x,y) Boundary Conditions: F=Fo for x=0 F=0 for x=a ∂F/∂y=0 for y=0 and y=b Homework Equations How can I find Eigengunctions of F(x,y) for expansion along Y in terms of X? The Attempt at a Solution I can't imagine...- Chingon
- Thread
- Boundary Poisson Poisson equation Value
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
K
Defenition of prior austenite grain boundary
What is prior austenite grain boundary?Grain boundary and prior austenite grain boundary are same terminology or different?I am confused:confused: Thanks- krautkramer
- Thread
- Boundary
- Replies: 2
- Forum: Materials and Chemical Engineering
-
S
Two-point boundary value problem
Homework Statement Solve the given BVP or show that it has no solution. (It does have a solution) y"+2y = x, y(0)=y(\pi)=0 Homework Equations Characteristic polynomial is r^2 + 2 = 0. μ = √2 The Attempt at a Solution The solution to the complementary homogeneous equation is y_h...- stgermaine
- Thread
- Boundary Boundary value problem Value
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
D
Graduate Boundary value problem - constrained paramter
Let's say I have a set of nonlinear differential equations of the form. x' = f(x,y) \\ y' = g(x,y) Where f and g contain some parameter 'a' that is constrained to within certain values. Let's say I know x(0), y(0) and x(T), y(T) where T isn't a set value. What methods can I use to...- Deadstar
- Thread
- Boundary Boundary value problem Value
- Replies: 2
- Forum: Differential Equations
-
L
Graduate Divergence Theorem on a surface without boundary
Reading through Spivak's Calculus on Manifolds and some basic books in Analysis I notice that the divergence theorem is derived for surfaces or manifolds with boundary. I am trying to understand the case where I can apply the divergence theorem on a surface without boundary. -
J
PDE Separation of Variables with Nonzero Boundary Conditions
Homework Statement Solve the diffusion equation: u_{xx}-\alpha^2 u_{t}=0 With the boundary and initial conditions: u(0,t)=u_{0} u(L,t)=u_{L} u(x,0=\phi(x) The Attempt at a Solution I want to solve using separation of variables... I start by assuming a solution of the form...- jtleafs33
- Thread
- Boundary Boundary conditions Conditions Pde Separation Separation of variables Variables
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
B
Graduate What Equation Models Boundary Layer Thickness in Early Stage Pipe Flow?
Hi I cannot find an equation for a boundary layer in a pipe flow (laminar). I am looking for an equivalent of the equation δ(x)=4.91x/(√Re) that works for a flow between plates (x is the distance downstream). The thing is- I am looking for BL thickness for still undeveloped flow. I would be... -
D
MHB Solution of the Damped Wave Equation under Certain Boundary Conditions
$$ u_{tt} + 3u_t = u_{xx}\Rightarrow \varphi\psi'' + 3\varphi\psi' = \varphi''\psi. $$ $$ u(0,t) = u(\pi,t) = 0 $$ $$ u(x,0) = 0\quad\text{and}\quad u_t(x,0) = 10 $$ \[\varphi(x) = A\cos kx + B\sin kx\\\] \begin{alignat*}{3} \psi(t) & = & C\exp\left(-\frac{3t}{2}\right)\exp\left[t\frac{\sqrt{9...- Dustinsfl
- Thread
- Boundary Boundary conditions Conditions Damped Wave Wave equation
- Replies: 16
- Forum: Differential Equations
-
E
Graduate How to set up Neumann boundary condition for a PDE in a coordinate-invariant form?
I'm having trouble finding out how to set up Neumann (or, rather, "Robin") boundary conditions for a diffusion-type PDE. More specifically, I have a scalar function f(\boldsymbol{x}, t) where \boldsymbol{x} is n-dimensional vector space with some boundary region defined by A(\boldsymbol{x})=0...- eugvas
- Thread
- Boundary Boundary condition Condition Form Neumann Pde Set
- Replies: 1
- Forum: Differential Equations
-
B
Laplace equation w/ dirichlet boundary conditions - Partial Diff Eq.
Homework Statement The steady state temperature distribution T(x,y) in a flat metal sheet obeys the partial differential equation: \displaystyle \frac{\partial^2 T}{\partial x^2}+ \frac{\partial^2 T}{\partial y^2} = 0 separate the variables in this equation just like in the...- bossman007
- Thread
- Boundary Boundary conditions Conditions Diff eq Laplace Laplace equation Partial
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
P
Fluid Dynamics - Spanwise Vorticity of Turbulent Boundary Layer
Hi all, Am reading a few papers for a Uni case study about structures in Turbulent Boundary Layers over a Flat Plate (water), particularly low-speed streaks. I'm confused over what mechanism causes the span wise variations in velocity that seems to cause low speed streaks. Would...- pobatso
- Thread
- Boundary Boundary layer Dynamics Fluid Fluid dynamics Vorticity
- Replies: 12
- Forum: Mechanical Engineering
-
C
Graduate Solve differential equation with boundary conditions using substitution
μ^{2}\frac{d^{2}u}{dx^{2}}+ae^{u}=0 Boundary conditions: u(-L)=u(L)=u_{0} Solve by multiplying by \frac{du}{dx} and integrating in x I know you have to use substitution, but I keep going in circles.- cheesecake91
- Thread
- Boundary Boundary conditions Conditions Differential Differential equation Substitution
- Replies: 2
- Forum: Differential Equations
-
H
Graduate What does this boundary condition mean?
One of the boundary conditions for a homogeneous uniform waveguide is \frac{\partial H_z}{\partial n}=0. What does this mean physically? -
D
Boundary Value Problem and Eigenvalues
Homework Statement y'' +λy=0 y(1)+y'(1)=0 Show that y=Acos(αx)+Bsin(αx) satisfies the endpoint conditions if and only if B=0 and α is a positive root of the equation tan(z)=1/z. These roots (a_{n})^{∞}_{1} are the abscissas of the points of intersection of the curves y=tan(x) and...- domesticbark
- Thread
- Boundary Boundary value problem Eigenvalues Value
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
D
MHB Boundary conditions spherical coordinates
Laplace axisymmetric $u(a,\theta) = f(\theta)$ and $u(b,\theta) = 0$ where $a<\theta<b$. The general soln is $$ u(r,\theta) = \sum_{n=0}^{\infty}A_n r^n P_n(\cos\theta) + B_n\frac{1}{r^{n+1}}P_n(\cos\theta) $$ I am supposed to obtain $$ u(r,\theta) = \sum_{n =...- Dustinsfl
- Thread
- Boundary Boundary conditions Conditions Coordinates Spherical Spherical coordinates
- Replies: 1
- Forum: Differential Equations
-
B
Graduate Boundary condition problem for diffusion equation
BOUNDARY CONDITION PROBLEM I have came up with matrix for numerical solution for a problem where chemical is introduced to channel domain, concentration equation: δc/δt=D*((δ^2c)/(δx^2))-kc assuming boundary conditions for c(x,t) as : c(0,t)=1, c(a,t)=0. Where a is channel's length...- brambram
- Thread
- Boundary Boundary condition Condition Diffusion Diffusion equation
- Replies: 3
- Forum: Classical Physics
-
B
Boundary condition problem for diffusion equation
Homework Statement BOUNDARY CONDITION PROBLEM I have came up with matrix for numerical solution for a problem where chemical is introduced to channel domain, concentration equation: δc/δt=D*((δ^2c)/(δx^2))-kc assuming boundary conditions for c(x,t) as : c(0,t)=1, c(a,t)=0. Where a is...- brambram
- Thread
- Boundary Boundary condition Condition Diffusion Diffusion equation
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
M
Solving boundary value problem (Wave Equation)
Homework Statement Show that the boundary-value problem $$u_{tt}=u_{xx}\qquad u(x,0)=2f(x)\qquad u_t(x,0)=2g(x)$$ has the solution $$u(x,t)=f(x+t)+f(x-t)+G(x+t)-G(x-t)$$ where ##G## is an antiderivative/indefinite integral of ##g##. Here, we assume that ##-\infty<x<\infty## and ##t\geq 0##...- mizzcriss
- Thread
- Boundary Boundary value problem Value Wave equation
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
C
Planar wave normally incident on dielectric boundary
PROBLEM: I am asked to consider a parallel polarized planar wave with frequency ω is normally incident on a dielectric boundary. The incident time average power flux P_i = 100 w/m^2. The first medium is free space and the second has vacuum permeability but ε=4ε_0. We are also given that the...- cfitzU2
- Thread
- Boundary Dielectric Wave
- Replies: 1
- Forum: Introductory Physics Homework Help
-
S
Linearity of boundary conditions
Homework Statement Using the definition of linearity to determine whether or not ech case is a linear homegeneous boundary condition: i.) Uxx(0,y)=Ux(0,y)U(0,y) ii.)Uy(x,0)=Ux(5,y) Homework Equations The Attempt at a Solution I know Uxx(0,y)=Ux(0,y)U(0,y) is not linear...- sarideli18
- Thread
- Boundary Boundary conditions Conditions Linearity
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
E
Undergrad Solving PDF with set boundary values
I am give probability distribution function f(x)=(e(-x/1000))/1000 of the time to failure of an electronic component in a copier The question is to determine the number of hours at which 10% of all components have failed. My solution: 1) PDF was integrated to obtain: f(x)= e(-x/1000)...- Ein Krieger
- Thread
- Boundary Pdf Set
- Replies: 3
- Forum: Set Theory, Logic, Probability, Statistics
-
P
Graduate Applying shooting method to 4nd two point value boundary problem
Hi, I was wondering if you can apply shooting method to a 4nd differential eq. two point value boundary problem, specifically I want to use this method to solve Euler-Bernoulli eq. EI y(4)(x)=f(x), y(0)=0,y'(0)=0,y(L)=0,y'(L)=0. Normally, if you have a 2nd order two point value...- pgioun
- Thread
- Boundary Method Point Shooting method Value
- Replies: 2
- Forum: Differential Equations
-
S
Effect of Prandtl Number on Thermal Boundary Layer
I'm currently having a bit of an intuitive problem understanding the Prandtl number effect on boundary layers and I'm hoping that someone can explain it better than what I've read in some heat transfer books. According to various HT books, a low Prandtl number means that heat diffuses quickly...- sanka
- Thread
- Boundary Boundary layer Thermal
- Replies: 3
- Forum: Mechanical Engineering
-
T
Interior and boundary of set of orthogonal vectors
Let "a" be a non zero vector in R^n and define S = { x in R^n s.t. "a" · "x" = 0}. Determine S^int , bkundary of S, and closure of S. Prove your answer is correct Attempt: Ok I am more sk having trouble proving that the respective points belong to its condition. Such as thr...- trap101
- Thread
- Boundary Interior Orthogonal Set Vectors
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
S
Graduate Boundary of nuclear material sample
we know that the full life of radioactive sample is infinity. and if we take one radioactive atom in the sample then it's full is measurable and short. it changes when when it emits sub atomic particles. which contradict each other. we need to know more. the dimension of radioactive constant...- shivakumar06
- Thread
- Boundary Material Nuclear
- Replies: 3
- Forum: High Energy, Nuclear, Particle Physics
-
P
Basic sturm liouville boundary problems
Homework Statement Compute the eigenvalues/functions of the given regular S-L problem f''(x)+λf(x)=0 0<x<π f(0)=0 f'(π)=0 2. The attempt at a solution First off, why is π not included in the given boundary if it tells you f'(x) at π? Now for my attempt: assuming λ=0...- Pi Face
- Thread
- Boundary
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
D
MHB Orthogonality of Eigenfunctions of Mixed Boundary Conditions
$$ \left.(\phi_n\phi_m' - \phi_m\phi_n')\right|_0^L + (\lambda_m^2 - \lambda_n^2)\int_0^L\phi_n\phi_m dx = 0 $$ where $\phi_{n,m}$ and $\lambda_{n,m}$ represent distinct modal eigenfunctions which satisfy mixed boundary conditions at $x = 0,L$ of the form \begin{alignat*}{3} a\phi(0) + b\phi'(0)...- Dustinsfl
- Thread
- Boundary Boundary conditions Conditions Eigenfunctions Mixed Orthogonality
- Replies: 2
- Forum: Differential Equations
-
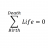
Boundary union and intersection problems
Homework Statement Let A, C \subseteq ℝn with boundaries B(A) and B(C) respectively. Prove or disprove : B(AUC) O B(A)UB(C) and B(A\capC) O B(A)\capB(C) Where O represents each of these symbols : \subseteq, \supseteq, = Homework Equations I know that double inclusion is going to cut the...- STEMucator
- Thread
- Boundary Intersection Union
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
R
D'Alembert question - boundary conditions parts
Homework Statement I have a general wave equation on the half line utt-c2uxx=0 u(x,0)=α(x) ut(x,0)=β(x) and the boundary condition; ut(0,t)=cηux where α is α extended as an odd function to the real line (and same for β) I have to find the d'alembert solution for x>=0; and show that in...- Ratpigeon
- Thread
- Boundary Boundary conditions Conditions D'alembert parts
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
I
Graduate Is there a problem in assuming the universe has a boundary?
I hear about the balloon analogy, and that there is no need to say that the universe has a boundary, but is that the only reason or would it be problematic to assume that space-time has a volume and a boundary?- id10tothe9
- Thread
- Boundary Universe
- Replies: 42
- Forum: Cosmology
-
V
Graduate Boundary conditions with dielectrics question
Hi all, I'm doing what should be a pretty simple problem, but some theory is giving me trouble. Basically, in this problem I have a conducting sphere, surrounded by a thick insulating layer, and then vacuum outside that. I'm attempting to solve for the potential in the insulating layer by...- VortexLattice
- Thread
- Boundary Boundary conditions Conditions Dielectrics
- Replies: 1
- Forum: Electromagnetism
-
R
Graduate PDE with oscillating boundary conditions
Hi, Say I have this pde: u_t=\alpha u_{xx} u(0,t)=\sin{x}+\sin{2x} u(L,t)=0 I know the solution for the pde below is v(x,t): v_t=\alpha v_{xx} v(0,t)=\sin{x} v(L,t)=0 And I know the solution for the pde below is w(x,t) w_t=\alpha w_{xx} w(0,t)=\sin{2x} w(L,t)=0 Would...- robl123
- Thread
- Boundary Boundary conditions Conditions Oscillating Pde
- Replies: 2
- Forum: Differential Equations
-
J
Graduate Neighborhood Retract of Boundary
Here is the problem: If M is a manifold with boundary, then find a retraction r:U→∂M where U is a neighborhood of ∂M. I realize the Collar Neighborhood Theorem essentially provides the desired map, but I am actually using this result to prove the aforementioned theorem. My thought on how to...- jgens
- Thread
- Boundary
- Replies: 2
- Forum: Differential Geometry
-
D
Graduate How does potential act as a boundary for electrons in infinite well
Im wondering how potential can act as a boundary for electrons in a 1-D time independent infinite well?- Dammes
- Thread
- Act Boundary Electrons Infinite Infinite well Potential
- Replies: 1
- Forum: Quantum Physics
-
H
Graduate Boundary condition for a charged surface
Hi, I am looking at a problem where I have two electrically conducting fluids where charge accrues on the interface, I know that one of the equations that I have to use comes straight from the usual boundary conditions for the normal component of the electric field, the other one apparent comes...- hunt_mat
- Thread
- Boundary Boundary condition Charged Condition Surface
- Replies: 4
- Forum: Electromagnetism
-
Z
Solving for C1 and C2: A Wave Function Boundary Condition
Homework Statement A one-dimensional wave function associated with a localized particle can be written as \varphi (x) = \begin{cases} 1- \frac{x^2}{8}, & \text{if } 0<x<4, \\ C_1 - \frac{C_2}{x^2}, & \text{if} \,x \geq 4. \end{cases} Determine C_1 and C_2 for which this wave...- zhillyz
- Thread
- Boundary Boundary condition Condition Function Wave Wave function
- Replies: 3
- Forum: Advanced Physics Homework Help
-
D
Difference between partical shear stress and boundary shear stress
Hi all, I am currently studying civil hydraulics in my civil engineering course and we are going through estimating critical shear stresses for sediments. I am confused about the difference between boundary shear stress and particle shear stress. In terms of estimating critical shear stress...- db725
- Thread
- Boundary Difference Shear Shear stress Stress
- Replies: 6
- Forum: General Engineering
-
E
Graduate Electromagnetic boundary condition
in electromagnetics , considering boundary conditions of dielectric and perfect conductor , inside conductor E = 0. So, there should not be any time varying magnetic field. But in many books i have seen that inside conductor normal component of B is 0 because there is no time varying magnetic...- erece
- Thread
- Boundary Boundary condition Condition Electromagnetic
- Replies: 2
- Forum: Electromagnetism
-
G
Periodic boundary conditions for 2d grid
Hello , i am trying to implement this algorithm for 2d grid. 1) i am not sure if my calculations are correct. 2 ) i don't understand how to return my final calculation ( how will i insert to the matrix i want (the 's' in this example) the new coordinates (xup,xdow,yup,ydown)). I mean ...- ggeo1
- Thread
- 2d Boundary Boundary conditions Conditions Grid Periodic
- Replies: 6
- Forum: Programming and Computer Science
-
A
Graduate Laplace equation with boundary condition
Good afternoon, I am a PhD student in motions of damaged ships. I am trying to find a solution of Laplace equation inside a box with a set of boundary conditions such that: ∇2\phi=0 \phix=1 when x=-A and x=A \phiy=0 when y=-B and y=B \phiz=0 when z=Ztop and z=Zbot I have tried...- ACG_PhD
- Thread
- Boundary Boundary condition Condition Laplace Laplace equation
- Replies: 1
- Forum: Differential Equations
-

Is 29 Too Late to Start a Career in Physics?
Is there any boundary of age for any jobs such as International labs, an academic carieer in university ? The reason why i ask you is that I'm at 29 and I still major in MSc physics or physics enginnering. To you, Is it a logical ? So,i have been lated to apply any job in U.S or Europe ...- woLfRam108
- Thread
- Age Boundary Limit
- Replies: 2
- Forum: STEM Career Guidance
-
C
Graduate Counting electromagnetic modes in a rectangular cavity and boundary conditions
The electric field in a cubical cavity of side length L with perfectly conducting walls is E_x = E_1 cos(n_1 x \pi/L) sin(n_2 y \pi/L) sin(n_3 z \pi/L) sin(\omega t) E_y = E_2 sin(n_1 x \pi/L) cos(n_2 y \pi/L) sin(n_3 z \pi/L) sin(\omega t) E_z = E_3 sin(n_1 x \pi/L) sin(n_2 y \pi/L)...- Coriolis1
- Thread
- Boundary Boundary conditions Cavity Conditions Counting Electromagnetic Modes Rectangular
- Replies: 1
- Forum: Electromagnetism
-
M
Graduate PDE Helmholtz eq. in 3D + boundary value)
Hi!This is a quite sophisticated problem, but it’s interesting and challenging! Consider the following case: Let’s say we have a 3-dimensional disk with a radius r_{2} and a thickness d (so it actually is a cylinder with a quite short height compared to radius). We’re interested in solving...- marqushogas
- Thread
- 3d Boundary Helmholtz Pde Value
- Replies: 2
- Forum: Differential Equations
-
E
EM wave at a plane dielectric boundary
i was studying incidence of EM wave at a plane dielectric boundary and encountered equations in the attachment . I just want to know if n2 > n1 then electric field amplitude at the boundary increases . So from where does this extra value comes ? n1 and n2 are intrinsic impedances of 1st and...- erece
- Thread
- Boundary Dielectric Em Em wave Plane Wave
- Replies: 1
- Forum: Electrical Engineering