Curvature Definition and 872 Threads
-

B Mechanism of Curvature of Space: Does it Happen Instantly?
Hi all, How does matter curve space (what's the mechanism)? Does this Curvature happen instantaneously or does it happen at light speed? Thanks in advance.- Deepak K Kapur
- Thread
- Curvature Curvature of space Mechanism Properties Relation Space Space and time
- Replies: 5
- Forum: Special and General Relativity
-

A Does gravitational time dilation imply spacetime curvature?
In a recent thread, the question came up of whether the presence of gravitational time dilation implies spacetime curvature. My answer in that thread was no: This was based on the obvious counterexample of observers at rest in Rindler coordinates in flat Minkowski spacetime; two observers at...- PeterDonis
- Thread
- Curvature Dilation Gravitational Gravitational time dilation Spacetime Spacetime curvature Time Time dilation
- Replies: 230
- Forum: Special and General Relativity
-
P
I Einstein's elevator: gravity without curvature?
This is a rather old issue, but one that has recently been on my mind. We often say that gravity is the curvature of space-time, with good reason. At the same time, we also talk about the "gravity" in Einstein's elevator, as an example of the equivalence principle. This is also with good...- pervect
- Thread
- Curvature Elevator Gravity
- Replies: 47
- Forum: Special and General Relativity
-
A
A Intution behind the definition of extrinsic curvature
Forgive me for asking a rather silly question, but I have thinking about the following definition of the extrinsic curvature ##\mathcal{K}_{ij}## of a sub-manifold (say, a boundary ##\partial M## of a manifold ##M##): $$\mathcal{K}_{ij} \equiv \frac{1}{2}\mathcal{L}_{n}h_{ij} =...- Afonso Campos
- Thread
- Curvature Definition Extrinsic
- Replies: 2
- Forum: Differential Geometry
-

B Einstein's curvature vs. Newton's
I've read that observations during the solar eclipse of 1919 showed that Einstein's prediction of light's curvature passing near the Sun was exactly twice that of Newton. I have two questions: 1. Why did Newton assume any curvature? Did he think "light particles" had mass? 2. In the physical...- Peter Martin
- Thread
- Curvature
- Replies: 22
- Forum: Special and General Relativity
-
D
I Use a level to test the Earth's curvature?
So, I'm sure many of you have seen the experiment recently by a flat-Earth member who brought a level on a plane with him in order to determine whether or not the Earth is flat or round. And yeah, my immediate thought was similarly "how silly!" But it did make me wonder: Could you do it that...- davee123
- Thread
- A level Curvature Test
- Replies: 12
- Forum: Other Physics Topics
-
A
I Understanding Parallel Transport
I'm currently in a GR class and have come across the notion of parallel transport, and I've searched and searched the last few days to try and understand it but I just can't seem to wrap my head around it, so I'm hoping someone here can clarify for me. The way I picture parallel transport is...- Arcturus7
- Thread
- Connection Curvature Parallel Parallel transport Transport
- Replies: 9
- Forum: Differential Geometry
-

Centre of curvature of a mirror and the perpendicular
If the normal is always 90 to the mirror can we assume that it always passes through centre of curvature? The light rays passing through the centre are reflected back in the same direction as angle of incidence is 0 and incident angle is 90 so, the normal should pass through the centre.- shihab-kol
- Thread
- Curvature Geometrical optics Light Mirror Perpendicular Reflection
- Replies: 1
- Forum: Optics
-

I Consequence of curvature of spacetime
I was wondering that consequence of curvature of spacetime caused by an entire galaxy! Can anyone suggest? -

I Mean and Gaussian curvature for a Gaussian 'hill' seem wrong
I'm hoping someone can help check whether my final contour plots look plausible based on the surface. I haven't done too much differential geometry but I've needed to work with Gaussian/Mean curvature for a simple 3D gaussian surface. Here's an example: (A = 7, a=b=1/(3.5)^2) It's...- Zaent
- Thread
- Curvature Gaussian Hill Mean Surface
- Replies: 6
- Forum: Differential Geometry
-

Radius of curvature of trajectory
Homework Statement a golfer hits a golf ball so that it has an initial velocity of 165mph and 12 degrees above the horizon. I already know the radius of curvature when the ball is hit. but my question is, will the radius be that same when it hits the ground? Homework Equations an=v2/ρ The...- Dusty912
- Thread
- Curvature Radius Trajectory
- Replies: 2
- Forum: Introductory Physics Homework Help
-

Radius of curvature of projectile path
Homework Statement The athelete releases the shot with velocity v = 16 m/s at 20° above the horizontal. What is the instantaneous radius of curvature of the shot’s path when it is at the highest point of its trajectory? Enter an answer in meters up to the first decimal place. Use g = 9.81...- Dusty912
- Thread
- Curvature Path Projectile Radius
- Replies: 4
- Forum: Introductory Physics Homework Help
-

Rainbow Curvature: Why is it Curved?
Jus a brief musing. I understand that light refracts showing the different colours when a rainbow is formed but have never known why they are curved rather than straight. Probably a simple explanation but not known to me. Can anyone explain please- simon willetts
- Thread
- Curvature Rainbow
- Replies: 8
- Forum: Other Physics Topics
-

I Curvature and the size of the Universe
I always have trouble understanding this concept. Please correct me if I am wrong somewhere in my line of thought. Is the universe finite or infinite? Using the famous balloon analogy, we can think of it as a finite expanding universe. But in that analogy the balloon has a curvature. Does the...- CassiopeiaA
- Thread
- Cosmology Curvature Universe
- Replies: 20
- Forum: Cosmology
-
T
Find the Riemannian curvature tensor component
Given the metric of the gravitational field of a central gravitational body: ds2 = -ev(r)dt2 + eμ(r)dr2 + r2 (dθ2 + sin2θdΦ2) And the Chritofell connection components: Find the Riemannian curvature tensor component R0110 (which is non-zero). I believe the answer uses the Ricci tensor...- Tom Weaver
- Thread
- Christoffel Component Cosmolgy Curvature Curvature tensor General relativity Riemman Schwarzchild Tensor
- Replies: 6
- Forum: Advanced Physics Homework Help
-
M
I Thin film around circle and ignoring curvature
Hi PF! If we have flow around a curved object that is sufficiently thin, I Have seen many texts assume the surface is linear rather than curved. Can someone help me with what "sufficiently thin" is quantitatively and how this allows us to neglect surface curvature? As a simple toy problem...- member 428835
- Thread
- Circle Curvature Film Thin film
- Replies: 6
- Forum: Classical Physics
-
R
I Curvature forms and Riemannian curvatures of connections
I'm trying to think of the curvature form of a connection on a tangent frame pricipal bundle as an alternative description of the Riemannian curvature of the connection(see i.e. https://en.wikipedia.org/wiki/Curvature_form) One thing I want to confirm is does a non-vanishing curvature-form...- RockyMarciano
- Thread
- Curvature Forms
- Replies: 53
- Forum: Differential Geometry
-
A
B How is the Horizon Drop Calculated Due to Earth's Curvature?
I propose a calculation of the drop X in the horizon that an observer sees due to the curvature of the Earth surface the parameters are: h: the elevation of the observer from the surface of the Earth in km H: the length of the horizon at which the drop is perceived in km R: the radius of the...- Axion
- Thread
- Curvature Earth
- Replies: 2
- Forum: Other Physics Topics
-
M
B What Would Happen in a Universe with Negative Curvature of Spacetime?
I know negative curvature of spacetime is close to impossible.. but reading about dark energy and how it is repulsive... I'm trying to find illustrations of what would happen when spacetime curvature is negative (locally as whole cosmos having negative curvature is different concept than local...- mieral
- Thread
- Curvature Negative
- Replies: 36
- Forum: Special and General Relativity
-

A Where is Potential Curvature Stored in GR?
It is commonly said that if you lift an object above the Earth it gains potential energy equal to mgh (m=mass, g=gravitational acceleration, h=height), suggesting that the potential energy is in the lifted mass. This cannot be. Consider the case of two perfectly rigid spheres, isolated in...- Thinkor
- Thread
- Curvature General relativity Gr Potential Potential energy
- Replies: 9
- Forum: Special and General Relativity
-
T
B How can we find the curvature of a star or planet?
Suppose we are watching a star that is spehrical. But we will see its one face that is toward us(suppose its not rotating). We will see that face to be plane circular. Is there any way we can find the curvature? or tell if its spherical or disk shaped ?- Tahmeed
- Thread
- Curvature Planet Star
- Replies: 4
- Forum: Astronomy and Astrophysics
-
M
Show curvature of circle converges to curvature of curve @ 0
Homework Statement Let γ : I → ℝ2 be a smooth regular planar curve and assume 0 ∈ I. Take t ≠ 0 in I such that also −t ∈ I and consider the unique circle C(t) (which could also be a line) containing the 3 points γ(0), γ(−t), γ(t). Show that the curvature of C(t) converges to the curvature κ(0)...- MxwllsPersuasns
- Thread
- Circle Curvature Curve Invariant
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-

B Gravity and the curvature of space
I am not sure I can express clearly my thoughts on this one, but I am going to try. The effect of mass on space, and the resulting gravity, is sometimes described, in a two dimensions graphic, as a bowling ball applying pressure on the surface of a mattress, or something equivalent. Thus, the...- Brunolem33
- Thread
- Curvature Curvature of space Gravity Space
- Replies: 15
- Forum: Special and General Relativity
-
S
I Why do planets follow the same curvature at both foci?
We are told that planets and comets orbit the sun in an ellipse (Kepler's 3 laws) as shown below: We are also told that according to Einstein's theory of gravity, there is no force applied. Implied is that the planets move in straight lines through curved space. We know that the effect of...- StandardsGuy
- Thread
- Curvature Curved space Ellipse Planets
- Replies: 12
- Forum: Astronomy and Astrophysics
-
L
A Interpretation of Derivative of Metric = 0 in GR - Learning from Wald
I am trying to learn GR, primarily from Wald. I understand that, given a metric, a unique covariant derivative is picked out which preserves inner products of vectors which are parallel transported. What I don't understand is the interpretation of the fact that, using this definition of the...- LarryL
- Thread
- Covariant derivative Curvature Derivative Interpretation Metric
- Replies: 2
- Forum: Special and General Relativity
-

A How was the value of the spacetime curvature obtained?
I received a reply about the value of space time curvature. Evidently it is not zero but an almost unconceiveably small number. I was just wandering how this number was gotten.- arupel
- Thread
- Curvature Spacetime Spacetime curvature Value
- Replies: 3
- Forum: Special and General Relativity
-

Finding the radius of curvature of trajectory
Homework Statement The functions are given: ##r(t)=pe^{kt}## ##\theta (t)=kt## ##v(r)=\sqrt2kr## ##a(t)=2k^2r## Find the radius of the curvature of the trajectory in the function of ##r## Homework Equations $$R=\frac{(\dot x^2 + \dot y^2)^{3/2}}{(\dot x\ddot y - \ddot x\dot y)}$$ There is also...- doktorwho
- Thread
- Acceleration Curvature Equations of motion Polar coordinates Radius Trajectory
- Replies: 7
- Forum: Introductory Physics Homework Help
-
L
I Meaning of the sign of the geodesic curvature
My question is : what is the meaning of the geodesic curvature sign for a coordinate patch? for a surface? Thank you.- Leo Mar
- Thread
- Curvature Geodesic Sign
- Replies: 3
- Forum: Differential Geometry
-

Osculating Circle Homework: Solving for Curvature Limit
Homework Statement I know I would use the curvature equation |f''| / [1-(f')^2]^3/2 and then take the limit of that to -1. I just don't understand why I have to take the limit of the curvature and when I take the limit of the curvature I get |-1| / (13)^3/2 when the answer should be 2.- Adeel Ahmad
- Thread
- Calculus 3 Circle Curvature
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
C
Curvature of r(t) = (3 sin t) i + (3 cos t) j + 4t k
Homework Statement [/B] find the curvature of the vector valued function r(t) = 3sint i + 3cost j +4t k Homework EquationsThe Attempt at a Solution For the unit tangent vector , i got T(t) = (3cost i -3sint j +4k) / sqrt (9 ((sint)^2 ) + 9 ((cost)^2 ) + 4^2 ) = (3cost i -3sint j +4k) / 5 For...- chetzread
- Thread
- Cos Curvature Sin
- Replies: 22
- Forum: Calculus and Beyond Homework Help
-

B Observational limit from the super-horizon mode spectrum
In making cosmological measurements, we are limited to the region within the particle horizon, the 'observable universe'. However, it is reasonable to assume that even if the universe is finite, it is much larger than that volume. If, for example, we measure the curvature ##\Omega_K##, the value...- GeorgeDishman
- Thread
- Curvature Limit Mode Spectrum
- Replies: 2
- Forum: Cosmology
-

I Understanding the curvature parameter k
1.) According to my understanding, k is a constant in the Robertson-Walker metric and the Friedmann equations. Its value (-1,0 or 1) is determined by observation (e.g. the bending of light) and doesn't change over time, unlike the curvature density parameter ##\Omega_k##. Therefore a strictly... -
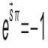
A The information about the curvature on the rest
What happens with the information about the curvature of the trajectory of a body when the body stops? We know that to assess the curvature of a path we must calculate the value of a fraction of which the denominator is speed module (cubed). But if speed module is canceled, this fraction can not...- Abel Cavaşi
- Thread
- Curvature Information Rest
- Replies: 23
- Forum: Other Physics Topics
-
D
Finding the curvature of a space curve
Homework Statement Find the curvature of the car's path, K(t) Car's Path: r(t) = \Big< 40cos( \frac {2 \pi}{16}t ) , 40sin( \frac {2 \pi}{16}t ), \frac{20}{16}t \Big> Homework Equations K(t) = \frac { |r'(t)\:X \:r''(t)|}{|r'(t)|^3 } The Attempt at a Solution This is part of a massive 6...- dlacombe13
- Thread
- 3d Calculus 3 Curvature Curve Parametric Space Vector
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-

B What was the curvature of the early universe?
I was reading about the first few Planck seconds and noticed no mention of general relativity other than the horizon problem. I some googling and only came up with some 1979 research that took the assumption that gravity was less powerful in the past, which I find suspect and Was developed...- newjerseyrunner
- Thread
- Curvature Early universe Universe
- Replies: 11
- Forum: Cosmology
-
P
I Can Hyperbolic Space be affecting our view of the universe?
Usually when gravitational lensing is discussed, the examples are those of matter bending spacetime into a positive curvature. https://commons.wikimedia.org/wiki/File:Gravitational_lens-full.jpg In these cases, distortion of light is clearly evident as images of galaxies from behind these...- particlezoo
- Thread
- Curvature Cyclic Gaussian Hyperbolic Space Spacetime Universe
- Replies: 18
- Forum: Special and General Relativity
-
S
What is the arc-length parameterization for a given vector function?
Homework Statement Find the arc-length parameterization for r(t)=\left< { e }^{ 2t },{ e }^{ -2t },2\sqrt { 2 } t \right> ,t\ge 0 Homework Equations s(t)=\int { \left| \dot { r } (t) \right| dt } The Attempt at a Solution \dot { r } (t)=\left< { 2e }^{ 2t },-2{ e }^{ -2t },2\sqrt { 2 }...- Sho Kano
- Thread
- arc length curvature parameter vector
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
S
Find the center of the circle of curvature
Homework Statement For the curve with equation y={ x }^{ 2 } at the point (1, 1) find the curvature, the radius of curvature, the equation of the normal line, the center of the circle of curvature, and the circle of curvature. Homework EquationsThe Attempt at a Solution \kappa \left( 1 \right)...- Sho Kano
- Thread
- center circle curvature normal vector
- Replies: 6
- Forum: Precalculus Mathematics Homework Help
-

B What Is the Physical Meaning of Curvature in General Relativity?
I'm new at this, trying to understand the overall picture of GR From what I understand space does not actually curve but rather test particles tracing out their world lines in Euclidean space as compared to ones tracing out their world lines near a source of gravity is the physical meaning of...- Megaton
- Thread
- Curvature Physical
- Replies: 46
- Forum: Special and General Relativity
-
N
B How come GR doesn't describe other forces with curvature?
Let me start by saying that I'm a physics student but I have no experience with GR other than some pop-sci and some clarifications on that pop-sci from various sources, so basically I'm saying that some math is fine but please bare in mind that I have no real experience with the relevant math...- nashed
- Thread
- Curvature Forces Gr
- Replies: 10
- Forum: Special and General Relativity
-
L
A Curvature of Flat Lorentz manifolds
While Minkowski space and Euclidean space both have identically zero curvature tensors it seems that a flat Lorentz manifold in general, may not admit a flat Riemannian metric. Such a manifold is the quotient of Minkowski space by the action of a properly discontinuous group of Lorentz...- lavinia
- Thread
- Curvature Differential geometry Flat Lorentz Manifolds
- Replies: 31
- Forum: Differential Geometry
-
T
Radius of Curvature to Correct Myopia
Homework Statement A person's eye has a near point of 7 cm. The cornea at the outer surface of the eye has a refractive index of n_c = 1.376 and forms a convex shape with a radius of curvature of R_2 = 8 mm against air. The figure below shows the same eye with a contact lens (refractive index...- TeslaCoil137
- Thread
- Curvature Eye Geometric optics Radius
- Replies: 3
- Forum: Introductory Physics Homework Help
-
C
How Is Curvature Calculated Using Vector Functions?
Homework Statement can someone explain how to turn the formula of curvature T'(t) / r'(t) into | r'(t) x r"(t) | / | (r't)^3 | ? Homework EquationsThe Attempt at a Solution my working is in 317.jpgT'(t) / r'(t) <blockquote class="imgur-embed-pub" lang="en" data-id="a/q3t1U"><a...- chetzread
- Thread
- Curvature Formula
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
J
A Prove Constant Curvature: Homogeneity Implied by Cosmological Principle
I'm currently on section 5.1 in Wald's book. He is trying to prove that the cosmological principle implies that space has constant curvature. Given a spacelike hypersurface ##\Sigma_t## for some fixed time ##t##, we say that it is homogeneous if given ##p,q \in \Sigma_t##, there is an...- JonnyG
- Thread
- Constant Curvature
- Replies: 8
- Forum: Special and General Relativity
-
F
I Black Hole & Spacetime Curvature: Can Mass Decrease It?
Since a black hole goes to a singularity, theoretically wouldn't added mass to that point decrease the spacetime curvature by increasing of the circumference, and then not have a loss in information.- Felix Quintana
- Thread
- Black hole Curvature decrease Hole Spacetime Spacetime curvature
- Replies: 4
- Forum: Special and General Relativity
-

I How Do You Correctly Apply Indices in Tensor Calculus for Curvature?
Here's what I'm watching: At about 1:35:00 he leaves it to us to look at a parallel transport issue. Explicitly to caclculate ##D_s D_r T_m - D_r D_s T_m## And on the last term I'm having some difficulties, the second christoffel symbol. So we have ##D_s [ \partial_r T_m - \Gamma_{rm}^t T_t]##...- BiGyElLoWhAt
- Thread
- christoffel symbols curvature tensor analysis
- Replies: 3
- Forum: Special and General Relativity
-

A Curvature tensor in all flat space coordinates
hi, I am just curious about, and really wonder if there is a proof which demonstrates that curvature tensor is 0 in all flat space coordinates. Nevertheless, I have seen the proofs related to curvature tensor in Cartesian coordinates and polar coordinates, but have not been able to see that zero...- mertcan
- Thread
- Coordinates Curvature Curvature tensor Flat Space Tensor
- Replies: 4
- Forum: Special and General Relativity
-
W
I Does positive curvature disprove eternal inflation?
According to this paper, eternal inflation would be falsified by positive curvature: http://arxiv.org/pdf/1203.6876v2.pdf However the proposer of eternal inflation, Alex Vilenkin, has suggested spontaneous creation of the universe from"nothing". Apparently this doesn't violate the conservation...- windy miller
- Thread
- Curvature Inflation
- Replies: 6
- Forum: Cosmology
-

I What is Planck curvature and its significance in the expansion of the universe?
I was reading a paper by Starobinsky on spectrum of relict gravitational radiation. He uses the term Planck curvature as follows "We construct a model in which the universe was perpetually in the quantum state with the radius of curvature of the order of Planck curvature, and later left this...- kini.Amith
- Thread
- Curvature Planck
- Replies: 1
- Forum: Special and General Relativity
-
V
I 3D space curvature visualization
I want to program space curvature vizualizaion. I want to have an observer as a player that moves in 3d curved space and surrounding objects that will show curvature by distortion when player passes near them. I am concerned about some points: 1. What curvature to choose in order to experience...- VladZH
- Thread
- 3d Curvature Space Space curvature Visualization
- Replies: 14
- Forum: Differential Geometry