What is Functional: Definition and 414 Discussions

In computer science, functional programming is a programming paradigm where programs are constructed by applying and composing functions. It is a declarative programming paradigm in which function definitions are trees of expressions that map values to other values, rather than a sequence of imperative statements which update the running state of the program.
In functional programming, functions are treated as first-class citizens, meaning that they can be bound to names (including local identifiers), passed as arguments, and returned from other functions, just as any other data type can. This allows programs to be written in a declarative and composable style, where small functions are combined in a modular manner.
Functional programming is sometimes treated as synonymous with purely functional programming, a subset of functional programming which treats all functions as deterministic mathematical functions, or pure functions. When a pure function is called with some given arguments, it will always return the same result, and cannot be affected by any mutable state or other side effects. This is in contrast with impure procedures, common in imperative programming, which can have side effects (such as modifying the program's state or taking input from a user). Proponents of purely functional programming claim that by restricting side effects, programs can have fewer bugs, be easier to debug and test, and be more suited to formal verification.Functional programming has its roots in academia, evolving from the lambda calculus, a formal system of computation based only on functions. Functional programming has historically been less popular than imperative programming, but many functional languages are seeing use today in industry and education, including Common Lisp, Scheme, Clojure, Wolfram Language, Racket, Erlang, Elixir, OCaml, Haskell, and F#. Functional programming is also key to some languages that have found success in specific domains, like JavaScript in the Web, R in statistics, J, K and Q in financial analysis, and XQuery/XSLT for XML. Domain-specific declarative languages like SQL and Lex/Yacc use some elements of functional programming, such as not allowing mutable values. In addition, many other programming languages support programming in a functional style or have implemented features from functional programming, such as C++11, Kotlin, Perl, PHP, Python, Go, Rust, Raku, Scala, and Java (since Java 8).

View More On Wikipedia.org
Recent contents Top users
  1. shihab-kol

    Glycolic acid functional group(s)

    Hey guys, should the -OH group in glycolic acid be considered a functional group or a substituent due to the presence of the carboxylic acid group?
  2. binbagsss

    Complex scalar field, conserved current, expanding functional

    Homework Statement [/B] Hi I am looking at this action: Under the transformation ## \phi \to \phi e^{i \epsilon} ## Homework Equations [/B] So a conserved current is found by, promoting the parameter describing the transformation- ##\epsilon## say- to depend on ##x## since we know that...
  3. A

    I Density Functional Theory and pseudopotentials

    Hi, I have a blog oriented on computational physics: https://compphys.go.ro For many posts I have a GitHub project. Lately I started some DFT oriented ones, the latest being a DFT (with plane waves basis) project for a 'quantum dot'. Currently I started working on a project that will use the...
  4. S

    I Norm of a Functional and wavefunction analysis

    Hi, I am working on a home-task to analyse the properties of a ODE and its solution in a Hilbert space, and in this context I have: 1. Generated a matrix form of the ODE, and analysed its phase-portrait, eigenvalues and eigenvectors, the limits of the solution and the condition number of the...
  5. Bishamonten

    Understanding functional derivative

    Homework Statement "The functional ## J[f] = \int [f(y)]^pφ(y)\, dy ## has a functional derivative with respect to ## f(x) ## given by: $$ \frac {δJ[f]} {δf(x)} = \lim_{ε \rightarrow 0} \frac 1 ε \left[ \int[f(y) + εδ(y-x)]^pφ(y)\, dy - \int [f(y)]^pφ(y)\, dy\right] $$ $$ =...
  6. U

    Functional Derivative with respect to Dirac Spinors

    Homework Statement I am currently working on an exercise list where I need to calculate the second functional derivative with respect to Grassmann valued fields. $$ \dfrac{\overrightarrow{\delta}}{\delta \psi_{\alpha} (-p)} \left( \int_{x} \widetilde{\bar{\psi}}_{\mu} (x) i \partial_{s}^{\mu...
  7. binbagsss

    Zeros of Riemann zeta function, functional equation and Euler product

    Homework Statement Question Use the functional equation to show that for : a) ##k \in Z^+ ## that ## \zeta (-2k)=0## b) Use the functional equation and the euler product to show that these are the only zeros of ##\zeta(s) ## for ##Re(s)<0## . And conclude that the other zeros are all located...
  8. Jianphys17

    Rigor in Quantum physics -- Do I need to know Functional Analysis well?

    Hello, I've a following question: Is necessary know well func. analysis, and all its theorems to handle well quantum physics...?
  9. T

    Differentiability and functional equations

    Homework Statement Let f((x+y)/2)= {[f(x)+f(y)]/2} for all real x and y {f'(x)=first order derivative of f(x)} f'(0) exists and is equal to -1 and f(0)=1. Find f(2) Homework Equations Basic formula for differentiablilty: f'(x)=limit (h tends to 0+) {[f(x+h)-f(x)]/h} The Attempt at a...
  10. binbagsss

    Generating Functional in Momentum Space -- QFT

    Homework Statement Hi, Question attached: inserting ##\phi (x)= \int \frac{d^4k}{(2\pi)^2}\phi(x)e^{-i k_u x^u}## and similar for ##J(x) ## / ##J(k)## into the action and then integrating over ##k## gives: Solution attached: I AM STUCK on this part, completing the square ; so I see...
  11. alfab

    The functional form for dependence of force on Current?

    I am working on a lab where we were measuring how magnetic force between two parallel conductors varies with current and the separation between the two conductors. I need to find a formula for the dependence of Force on current to create a fit line on the data in my graph that shows the relation...
  12. Tbonewillsone

    Deriving an influence functional is deriving me mad (Help)

    Homework Statement I am attempting to derive Caldeira-Leggett's influence functional found in their paper "Path Integral Approach To Quantum Brownian Motion". If you find my following statements confusing, then pages 16-18 of http://web.science.uu.nl/itf/Teaching/2006/MxWakker.pdf show the...
  13. D

    I What is a Functional in Mathematics?

    I have read the wiki page (https://en.wikipedia.org/wiki/Functional_(mathematics) but it is not helping. I understand what a regular function is input > do something to that input > output. but not what functional is, Wikipedia says "from a vector space into its underlying field of scalars"...
  14. vishal.ng

    A Taylor series expansion of functional

    I'm studying QFT in the path integral formalism, and got stuck in deriving the Schwinger Dyson equation for a real free scalar field, L=½(∂φ)^2 - m^2 φ^2 in the equation, S[φ]=∫ d4x L[φ] ∫ Dφ e^{i S[φ]} φ(x1) φ(x2) = ∫ Dφ e^{i S[φ']} φ'(x1) φ'(x2) Particularly, it is in the Taylor series...
  15. S

    A Evaluation of functional determinants

    Consider the evaluation of the following functional determinant: $$\text{log}\ \text{det}\ (\partial^{2}+m^{2})$$ $$=\text{Tr}\ \text{log}\ (\partial^{2}+m^{2})$$ $$= \sum\limits_{k} \text{log}\ (-k^{2}+m^{2})$$ $$= VT \int\frac{d^{4}k}{(2\pi)^{4}}\ \text{log}\ (-k^{2}+m^{2})$$ $$= iVT...
  16. naima

    B How do we obtain a Taylor expansion of a non-linear functional?

    Hi PF I try to understand how we get get a Taylor expansion of a non linear functional. I found this good paper here F maps functions to scalars. F[f] is defined. It has not scalars as arguments. I agree with A13 and A18. In another paper (in french) skip to page 9 the fisrt term is ##\int dx...
  17. binbagsss

    I Integration - chain rule / functional

    I have ## \int_{t = 0}^{t = 1} \frac{1}{x} \frac{dx}{dt} dt = \int_{t = 0}^{t = 1} (1-y) dt ## [1] The LHS evaluates to ## ln \frac{(x(t_0+T))}{x(t_0)} ##, where ##t_{1}=t_{0}+T## My issue is that, asked to write out the intermediatary step, I could not. I am unsure how you do this when the...
  18. G

    Find Unknown Values in Table | Functional Relevance Homework

    Homework Statement theres a table x - 1;2;3;u;u;u;u;8 y - 370;160;90;u;24;u;u;u u - unknown value i have to complete this table with this equation y=(k/x)+b you have to find k and b values Homework Equations y=(k/x)+b x is relevant to y...
  19. A

    Calculus of Variations: Functional is product of 2 integrals

    Homework Statement Minimize the functional: ∫01 dx y'2⋅ ∫01 dx(y(x)+1) with y(0)=0, y(1)=aHomework Equations (1) δI=∫ dx [∂f/∂y δy +∂f/∂y' δy'] (2) δy'=d/dx(δy) (3) ∫ dx ∂f/∂y' δy' = δy ∂f/∂y' |01 - ∫ dx d/dx(∂f/∂y') δy where the first term goes to zero since there is no variation at the...
  20. August

    Density Functional Theory (DFT) textbooks

    I'm starting out on DFT right now. I'm an experimental Physics student, so I'm not very familiar with theories. Can you recommend any good textbooks or resources that I can utilize for my study?? Thanks in advance.
  21. O

    I What is a Functional? Definition & Uses

    In the calculus of variations, the integral itself is a "functional." It depends on the form of the function of the Lagrangian: q and q-dot But I have seen this word "functional" used elsewhere in different contexts. I have seen: "A functional is a real valued function on a vector space." I...
  22. T

    Functional groups in this compound

    Homework Statement Homework EquationsThe Attempt at a Solution I counted 4 functional groups. I got: -Carboxylic acid -Ketone -Alcohol -Ether However, this combination is not available. I was wondering if phenol is a functional group as C seems the most likely option. I thought phenyl is a...
  23. binbagsss

    Chain rule / Taylor expansion / functional derivative

    Homework Statement To show that ##\rho(p',s)>\rho(p',s') => (\frac{\partial\rho}{\partial s})_p\frac{ds}{dz}<0## where ##p=p(z)##, ##p'=p(z+dz)##, ##s'=s(z+dz)##, ##s=s(z)## Homework Equations I have no idea how to approach this. I'm thinking functional derivatives, taylor expansions...
  24. Jianphys17

    Courses Gd of curve and surfaces or functional analysis before?

    Hello everyone, i just finished a course of analysis(2)\vector calculus.Now iI'm interested in doing Gd of curves and surfaces(Do Carmo), and functional analysis(Rudin'sbook), but do not know what may have precedence between the two, on which i should start before you think?
  25. F

    I Spatial homogeneity and the functional form of two-point functions

    Consider a two-point function $$f(\mathbf{r}_{1},\mathbf{r}_{2})$$ If one requires homogeneity, then this implies that for a constant vector ##\mathbf{a}## we must have $$f(\mathbf{r}_{1},\mathbf{r}_{2})=f(\mathbf{r}_{1}+\mathbf{a},\mathbf{r}_{2}+\mathbf{a})$$ How does one show that if this is...
  26. arpon

    Functional relation between u(x,y,z) and v(x,y,z)

    Homework Statement Let ##u## and ##v## be differentiable functions of ##x,~y## and ##z##. Show that a necessary and sufficient condition that ##u## and ##v## are functionally related by the equation ##F(u,v)=0## is that ##\vec \nabla u \times \vec \nabla v= \vec 0## Homework Equations (Not...
  27. Jonas Hall

    A Functional equation f(x)^n f(a - x) = 1

    Hi, In a problem I have been working on for a while now I have found that I want to find the function satisfying the functional relation f(x)n f(a - x) = 1 for n = 1 I believe I have proven that f(x) = x/(a - x). On this page is an answer I do not quite understand. One of the prerequisits...
  28. Conservation

    Interesting compounds with alcohol functional group

    I'm looking for examples of some interesting compounds that contain alcohol functional group (please, no joke suggestions about various liquor). Bonus points for creativity/thinking-outside-the-box. Thanks.
  29. W

    Variation of a Functional with Boundary Conditions

    Homework Statement Consider the functional ##S(a,b) = \int_0^∞ r(1-b)a' \, dr ## of two functions ##a(r)## and ##b(r)## (with ##a' = \frac{da}{dr}##). Find the ##a(r)## and ##b(r)## that extremize ##S##, with boundary conditions ##a(∞) = b(∞) = 1##. Homework EquationsThe Attempt at a Solution...
  30. S

    MHB Help with functional analysis questions

    Hi, Could someone post a solution to the following questions : 1. Let R be the real numbers and A a collection of all groups that are either bound or their complement is bound. a. Show that A is an Algebra. Is it a sigma algebra? b. Define measure m by m(B) = {0 , max(on B) x <...
  31. evinda

    MHB Applied Functional Analysis: What You Need to Know

    Hello! (Wave) What is Applied Functional Analysis about? What knowledge is required? Which is the difference between this and Functional Analysis ?
  32. S

    MHB Help for test - functional analysis

    Hi - my professor in functional analysis posted 4 prior years tests just 4 days before the test without solutions. I'd appreciate if anyone can help send solutions for the following with the following questions : 1. $\mu$ is a sigma additive measure over sigma algebra $\Sigma$. A $\in...
  33. S

    MHB What is a Semigroup and How Does it Relate to Immeasurable Sets?

    Hi, I'm taking a course in functional analysis and having some trouble with the following questions : 1. L1(R) is the space of absolutely integrable functions on R with the norm integrate(abs(f(x)) over -inf to +inf. Define a linear operator from L1(R) to L1(R) as A(f)(x)=integrate...
  34. ShayanJ

    Is the Born Rule Functional in Quantum Field Theory?

    In QFT, we can work with functionals of fields ##\Psi[\phi(x)]=\langle \phi | \Psi \rangle## that give us the probability amplitude for the field to be ## \phi(x) ##. It seems to me that the Born rule we get here i.e. ##P(\phi(x))=|\Psi[\phi(x)]|^2=|\langle \phi | \Psi \rangle|^2## is not of...
  35. F

    Functional analysis, ortho basis, weakly convergent

    Homework Statement This is a problem from Haim Brezis's functional analysis book. Homework EquationsThe Attempt at a Solution I'm assuming (e)n is the vectors like (e)1 = (1,0,0), (e)2=(0,1,0) and so on. We know every hilbert space has an orthonormal basis. I also need to know the...
  36. Ravendark

    Functional derivative of effective action

    1./2. Homework Statement In my QFT lecture we were introduced to the 1PI effective action ##\Gamma[\varphi]## for a scalar theory (in Euclidean space-time). In one-loop approximation we've found \Gamma^{(\text{1-loop})}[\varphi] = S[\varphi] + \frac{1}{2} \operatorname{Tr} \log D^{-1} where...
  37. S

    Quantum Functional Integration and Feynman rules

    Hallo Everybody, I am searching for a book (or lecture notes) that details the calculations that lead me from a given Lagrangian to the Feynman rules of the theory. It should not be rigouros, just the main steps to get the Feynman rules. Thanks for your help!
  38. L

    Functional equation Riemann Zeta function

    There are two forms of Riemann functional equation. One is more symmetric and follows from the other and the duplication theorem of the Gamma function. At least, that's been claimed here...
  39. Urs Schreiber

    Insights Higher Prequantum Geometry III: The global action functional - cohomologically - Comments

    Urs Schreiber submitted a new PF Insights post Higher Prequantum Geometry III: The Global Action Functional - Cohomologically Continue reading the Original PF Insights Post.
  40. G

    Is There a Positive Scalar That Can Make One Function Greater Than Another?

    Homework Statement Let ##f,g## be two real valued functions, defined on the segment ##[a,b]## and continuous on ##[a,b]##, such that ## 0 < g < f ##. Show there exist ##\lambda > 0 ## such that ## (1+\lambda) g \le f ## Homework Equations The Attempt at a Solution Set ##h = f/g##. Since...
  41. ShayanJ

    Functional time-dependent perturbation theory

    Today, in my advanced particle physics class, the professor reminded the time-dependent perturbation theory in NRQM and derived the formula: ##\displaystyle \frac{da_m(t)}{dt}=-i \sum_n e^{-i(E_n-E_m)} \int_{\mathbb R^3}d^3 x \phi^*_m (\vec x) V(\vec x,t) \phi_n(\vec x)##. Then he said that...
  42. J

    Functional Back Brace for Costume

    Hi, hopefully this is in the right place. I have big plans for making a Velociraptor costume and I've got a handle on how I'm putting most of it together, but there is one issue and it's a big one; comfort. I know that I'm going to be uncomfortable in the costume regardless of what I do and I'm...
  43. T

    Course selection: Functional Ceramics vs Principles of Metal

    Hi What is more beneficial as a graduate course? Functional Ceramics vs Principles of Metal Forming? Please tell me what you think Thanks a lot
  44. avikarto

    Multivariable IBP in the variation of a functional

    Let's call our functional $$F[f]=\int dx\:A\left(x,f,f',f''...\right)$$ We know that the variation of F can be written as $$\delta F=\int dx\:\left[\frac{\partial A}{\partial f}\delta f+\frac{\partial A}{\partial f'}\delta f'+...\right]$$ If i wanted to get everything in terms of delta f in...
  45. Ravendark

    Second functional derivative of fermion action

    Homework Statement [/B] Consider the following action: $$\begin{align}S = \int \mathrm{d}^4 z \; \bar\psi_i(z) \, (\mathrm{i} {\not{\!\partial}} - m)_{ij} \, \psi_j(z)\end{align}$$ where ##\psi_i## is a Dirac spinor with Dirac index ##i## (summation convention for repeated indices). Now I would...
  46. AXidenT

    Functional Analysis or Differential Geometry?

    I'm in my last semester of my undergraduate majoring in mathematics (focusing on mathematical physics I guess - I'm one subject short of having a physics major) and am wondering, largely from a physics perspective if it would be better to do a functional analysis course or a differential...
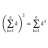
  47. ddd123

    Sterman's QFT - 2.7b (on functional derivatives)

    I've been trying to fill in my mathematical blanks of things I just took as dogma before. Especially, not having a background in functional analysis, the functional derivatives often seem to me mumbo jumbo whenever things go beyond the "definition for physicists". In particular I tried looking...
  48. SrVishi

    Analysis Principles to Real and Complex and Functional

    I'm reading Rudin's principles and so far I really like it. I find charm I'm his terseness, and I think having that motivation to do a lot of the stuff myself makes it pretty fun (like only using the outline of the Dedekind cuts section and prove all the steps myself). However, I have heard not...
  49. ShayanJ

    Integral kernel in vacuum wave functional

    I'm trying to solve the exercise below in a book I'm reading. I inverted equation 1.3 to get ## \phi_{\mathbf k}(t)=\int \frac{e^{-i \mathbf k \cdot \mathbf x}}{(2\pi)^{\frac 3 2}} \phi(\mathbf x,t) d^3 \mathbf x ##. Then I put it in I to get: ## I=\int \int d^3 \mathbf x d^3 \mathbf y...
  50. A. Neumaier

    Functional dependence of the size of the visible universe

    I am looking for reliable information about the functional dependence of the diameter ##d(t)## of the visible universe on the time ##t## since the big bang singularity, based on the different hypotheses currently deemed competitive.
Back
Top