sushi362
- 5
- 0
Homework Statement
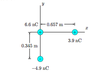
Consider three charges in a triangle as shown.
1. What is the net electric force on the charge at the origin?
2. What is the direction of this force(between -180 and 180)?
3. What is the magnitude of the net electric field at the position of the charge at the origin?
4. What is the direction of the net electric field?
Homework Equations
E = Kc * Q/r^2
The Attempt at a Solution
I solved part 1, to be 2.5*10^-6
part 2 is -102.38
i have no clue what to do for part 3.
once i figure that out, i should be able to do part 4.