Why Road Capacity Is Almost Independent of the Speed Limit
Let us start with a familiar situation. Take a familiar part of a road, for example, the one from your home to work. How long will it take you to drive from one end of that stretch of the road to the other? At times you will have the road almost to yourself and will be able to drive at the maximum allowed speed without any problem. At other times you will end up in a queue that moves extremely slowly – in fact, you may be standing still for quite some time. Why?
Table of Contents
Creating a simple model
As in all physics problems, let us start by defining our problem set. We will start by assuming that our road is a simple lane (no room for passing). We also assume that our drivers follow the “1001 – 1002 – 1003” rule (meaning that there should be a 3-second interval between the cars on the road). We shall also only consider the steady-state situation, leaving the dynamics problem for a later insight.
Measuring the interval from the front bumper to the front bumper
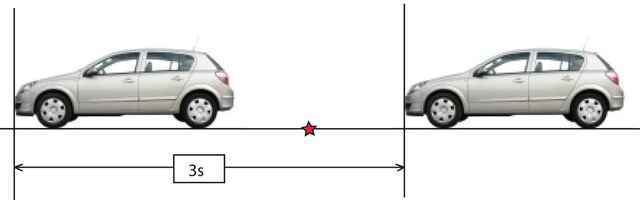
Figure 1. Two cars with a minimum interval
Figure 1 illustrates one way of measuring the time interval between cars. We have defined a “measuring point” on each car (here it is the front bumper) and measure the time interval between the front bumper of the first car passing an arbitrary point in the road to the following car passing the same point. Let us see what this measurement method implies.
- Since the minimum time interval between cars is 3 seconds, our measurement method implies that the maximum number of cars that can pass an arbitrary point on the road is one car every 3 seconds. One car every 3 seconds equals 20 cars every minute or 1200 cars every hour. The road capacity is therefore 1200 cars/hour
- Since the actual speed of the cars has not entered the calculations, we must conclude that the road capacity is independent of the speed limit. In other words: A local road with a speed limit of 50km/h has the same capacity as one lane on a highway with a speed limit of 100km/h.
- By the same reasoning, the maximum road capacity between two points depends only on the number of independent lanes, not on the speed limit. Thus, if one lane is blocked for some reason (accident, road work…), the road capacity is reduced accordingly.
Measuring from back bumper to front bumper
The measurement method given in Figure 1 has some serious problems at low speeds. One unintended consequence is that it assumes that all cars occupy the same space when they are standing still – which is of course impossible. To get better precision, we must modify our measurement method somewhat.
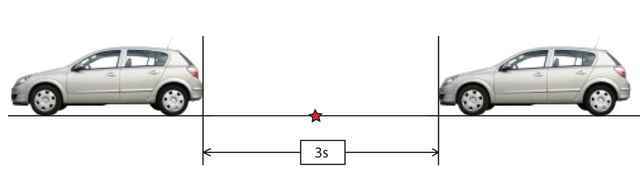
Figure 2. A better measurement method
Figure 2 shows a better way of measuring the time interval between cars. Now we will measure the time interval from the rear bumper of the first car passing an arbitrary point in the road to the front bumper of the following car passing the same point. This method solves the low-speed problem, but it is harder to analyze.

Figure 3. Road capacity as a function of queue speed
Figure 3 shows a calculation of the road capacity under the simplifying assumption that all cars are 5m long. From the curve, we see that:
- From about 60km/h, the road capacity is largely independent of the average car speed.
- When the average car speed falls below 30km/h, the road capacity falls drastically
Looking at the curve, we see that the road capacity at 25km/h is only 85% of the road capacity at 100km/h. One consequence is that a road that is at 90% of total capacity at 100km/h suddenly is overloaded if the average speed goes below 25km/h!
Some questions about road capacity
It may seem strange that the road capacity is more or less independent of the speed limit. After all, the time spent driving from A to B goes down as the speed limit goes up. So why does the capacity not increase?
The problem lies in getting onto the road in the first place. If the road is 100% full, you cannot get onto the road and start driving. If it is below 100%, you must still wait for an opportunity to get onto the road.
If the road is at full capacity, there are still no queues (by definition). So how does a queue form?
There are several reasons for queues forming. The most common is for cars trying to get onto a road that is already close to 100% full. Usually, this forces a car on the road to brake to keep the correct distance between cars. Since a speed reduction lowers the road capacity (Figure 3), this can suddenly cause the road to be more than 100% full.
Some observations about queues
Now assume that we have a queue on the road, a queue so bad that the cars are standing still. Assume that the average space a car occupies on the road when standing still is 5m.
Now take a collection of 50 cars that together utilize a stretch of road at full capacity.
- At an average speed of 80km/h, this collection occupies 3.6km of the road
- At an average speed of 50km/h, they occupy 2.3km
- And when they are standing still, they occupy 250m
Now, assume that the car collection drives happily along at 80km/h. Then something drastic happens, and the first car must go to a full stop. Going from 80km/h to a full stop (standard braking, no panic), takes about 14 seconds. The cars behind must also brake to a full stop, and since they come in 3s intervals, it takes about 160 seconds to bring the whole collection to a full stop. And, as noted above, they are now occupying 250m of the road.
Now assume that the first car can start up again, accelerating to full speed. When is the whole collection of cars back at 80km/h?
At this moment we need to consider the human element. The driver has to decide when it is “safe” to start up and increase the speed. This decision will vary among the individual drivers, but an informal measurement in front of the red light indicates that the average delay for such a decision to be made is about 1 second.
Final words
I have tried to show that the road capacity is almost independent of the speed limit and it depends almost exclusively on the number of lanes in each direction. What I have not touched is the dynamic response of a collection of cars on that road. So, who is going to do that?
Master’s in Mathematics, Norway. Interested in Network-based time synchronisation.






I spent 25 years driving in rush hour traffic in Chicago and spent much of that time in traffic thinking about what was causing the slow downs. First I agree with most of the article, disagree with a few things and believe I can offer a few insights.
Beginning with Creating a simple model, drivers in Chicago do not leave a three second interval between cars. Drivers in Chicago limit the space they leave between them and the car ahead of them to prevent a car from an adjacent lane from cutting in front of them. I have driven 80 mph with little more than a car length between me and the car ahead and so was everyone else. In Chicago the distance between cars is constant with regard to speed. This means that as the speed increases, highway capacity also increases.
The obvious solution for traffic jams is to raise the speed limit during rush hour to increase capacity but look what happens when there is an accident or debris in the road. Traffic slows down. When it slows down, drivers are unwilling to reduce the space between them and the next car. That reduces capacity which causes the speed to reduce to the point where drivers reduce the distance between them and the car ahead. That point is almost a dead stop. So when a highway is saturated, anything that slows traffic even a little can bring everybody to a complete stop.
There is another aspect that adds to the danger. When the car ahead brakes and there is so little space between cars, the car behind has a short reaction time so he must brake slightly harder than the car ahead of him to avoid hitting him. Each successive car must brake a little harder too until either somebody gets back-ended or someone has left enough space to allow him to stop in time.
Leaving more space between cars is a good solution but would never work in Chicago, I’ve tried it. Cars constantly pull in front of you and the cars behind you get mad. The only thing I can think of to reduce traffic jams is more lanes. There should be an algorithm for so many houses in a residential area there must be so many lanes in the highways serving it.
Nice article!
[QUOTE="mfb, post: 5576048, member: 405866"]Restarting traffic gets very tricky in that case.[/QUOTE]Ha Ha. They would have to get into different cars, at the other end. Human nature would be the only reason for not having a system like that.
[QUOTE="sophiecentaur, post: 5575939, member: 199289"]The inverse law of capacity with speed could be taken to ridiculous extremes if people got out of their cars and walked. The capacity would be in thousands but it would take you all day just to walk to and from work.[/QUOTE]Restarting traffic gets very tricky in that case.The road capacity for pedestrians on an empty road should be above 10,000 per lane.
Sounds like DERR, delayed effect road rage :-)
[QUOTE="houlahound, post: 5575958, member: 551046"]Smart[/QUOTE]Dumb, actually – and it shows the problem when taking situations to extremes. But I just don't care as I am remembering my hold up yesterday when driving through Southend. Average traffic speeds in Central London are frequently only walking place, or so they say,
Smart signs appear more efficient at improving traffic flow management than making new roads, directing people in real time as to what lane and what speed, rerouting etc.
The inverse law of capacity with speed could be taken to ridiculous extremes if people got out of their cars and walked. The capacity would be in thousands but it would take you all day just to walk to and from work.
Here are some thoughts on the dynamics of road capacity.Consider a part of the road which is near 100% capacity. This means that there is a finite number of cars (surprise!) and that there is a first car. Assume that the driver in the first car sees the need to brake rather suddenly and then accelerates back up and continues as before. The driver in the next car sees the braking lights on the car in front of him, but his reaction time brings him too close to the car in front. He therefore brakes too hard, and when the car in front accelerates back up, he accelerates too hard in order to keep the optimum distance. The driver in the third car…I suspect that a first order description will be close to the physical phenom of longitudinal waves in a spring with distributed masses along the spring. The current speed limit takes the place of g in the derivation, but instead of the damping you will have in a spring, you get a small amplification. That will explain why a sudden braking in front of a queue results in a full stop some 50 cars behind…I hope somebody with more time and a better knowledge of wave equations related to physical phenomena can do something sensible about these thoughts.
[QUOTE="mfb, post: 5573347, member: 405866"]In subway systems, most people don't care if they arrive a minute earlier or later – they have to wait for the train anyway. Some people care a lot because they might miss their connection if they are a minute late. So let those people rush, even if it means others (who have to wait anyway) are a bit slower.[/QUOTE]That isn't my experience. People are always hurrying as a matter of principle in order to be on the platform before the next train leaves. They don't know the time of arrival so they go as fast as they can – pushing old gimmers like me out of the way in their hurry. Then, of course, statistically, they are as likely to have to wait the same time as I would (I could possibly have missed the train that they caught.)
How to control the speed while driving in a car from accidentsl
In subway systems, most people don't care if they arrive a minute earlier or later – they have to wait for the train anyway. Some people care a lot because they might miss their connection if they are a minute late. So let those people rush, even if it means others (who have to wait anyway) are a bit slower.
This is an interesting piece of work and it makes a good attempt to formalise something that affects us all. The result is not intuitive and that makes it a valuable study. The Insight correctly points out that this is a complicated business and it is important to decide what we actually want from a stretch of road. It's dealing with Human Beings that makes it so complicated.Road capacity is basically a parameter for road designers but journey time is the parameter that drivers are interested in (or so they think). There are many parallels with what happens in DC electric circuits. In circuits, we are no often concerned with transit time for any individual charge. But charges don't care how fast they get round the circuit; it's the current capacity that's of interest to the Power Engineer. 'Road capacity' governs how quickly you can join a road and this is particularly relevant if you are joining a long stretch of road that's at full capacity but when you are only on it for a short stretch.Flexible speed limits on nominally fast roads seem to work OK (M25 London Orbital Motorway, UK, which is very subject to delays), despite the wingeing by many drivers when they have to drop back to 40mph. Greg's link, above, shows this to be the experience in the US. Speed and frequency / length of accident delays are almost certainly strongly correlated. High speed collisions cause much greater delays than simple sub-30mph shunts. That should be factored into any more detailed analysis, which would be difficult but not impossible as some statistics must be available.Like taxes and many of our laws, behaving well on roads is something that doesn't come naturally and it has to imposed on drivers (all of us). It's a hearts and minds business and needs to be treated that way if any real improvements are to be made.Related info: I recently heard (BBC Radio 4) of a study that was done on the capacity of long double width escalators on the London (I think it was) tube system. The convention is that you stand on the right and walk up on the left. In an experiment, they forbade any walking on the left so everyone was standing. It was found that the capacity of the escalator improved significantly. But that, of course, is not perceived as helping anyone who happens to be in a hurry – even if it may help them in the long run (pun?).
[QUOTE=".Scott, post: 5560594, member: 489053"]The article also fails to note the "rubber-necking" affect. One one of two lanes is blocked, the capacity of the remaining lane drops as curious drivers what to know why they were delayed by 30 minutes.[/QUOTE]This part of the dynamic response of the traffic. It is complex, that is why I invited in others to do that part.
I would say road capacity can be increased with higher speed while at the same time reducing distance between vehicles. That could work if every commuter was a highly trained stunt driver, but in practice it means automation. And not just independently controlled self-driving cars responding only to their immediate surroundings but fully networked and coordinated control for every car on the road, no human driving at all. This could be implemented gradually, one piece of road at a time, as self-driving cars become more commonplace.
I often measure the between cars – perhaps because I just finished teaching two of my kids how to drive. In my part of the world (southern New Hampshire, USA), the 3-second rule applies during very light traffic. It quickly drops to the 2-second rule with moderate traffic. On the limited access highways, it get get well below 2 seconds.Of course, the smaller the bumper-to-bumper time period, the greater is the effect of the cars dimension (~5m).As others have noticed in posts above, some driving periods are better than other. In general, rush hour is populated with drivers who keep up their speed and act to keep traffic moving smoothly.The article also fails to note the "rubber-necking" affect. One one of two lanes is blocked, the capacity of the remaining lane drops as curious drivers what to know why they were delayed by 30 minutes.
An analogy may be made to the hydraulic jump in fluid mechanics. High speed flow in a thin layer (vehicles with large spaces) switching to low speed flow in a thick layer (small spaces between vehicles.)On the few occasions I visit large cities, I have to grit my teeth driving. I'm retired, and know that my reactions are slow. I tend to leave a 3-4 second gap in front of me. In the city, gaps are much less than this — less than a second much of the time. If I try to keep my comfortable opening, I have to travel substantially slower than the traffic. People pass me in the other lane, and drift into *my* space. In effect I create a 'traffic shadow'
[QUOTE="mfb, post: 5556140, member: 405866"]That is not the main point. Drivers tend to over-react, and brake later and more than necessary.There are many simulations where you can study traffic flow for various different parameters, e.g. http://www.traffic-simulation.de/. Large decelerations increase the risk of a jam.[/QUOTE]Yes. I said that I described a steady-state situation. Your comment pertains to the dynamic response of cars on the road.[QUOTE="rcgldr, post: 5555278, member: 17595"]I'm wondering about the effect that speed has on how many cars there are on a freeway at any moment in time. At higher speeds, a commuter spends less time on the freeway (since the destination / freeway exit is reached sooner), which should result in fewer cars on the freeway at any moment in time.[/QUOTE]Yes. As I mentioned in the Insight, with a high speed limit a car goes faster from A to B when it has gotten onto the road. The problem lies in getting onto the road. If it is full (saturated), you cannot get onto it. If it is less than full, you must wait for an opening.
For very large speeds, a quadratic safety distance would be more conservative (to allow you to brake even if the car in front of you suddenly hits a wall), but drivers rarely follow that.[quote]There are several reasons for queues forming. The most common is for cars trying to get onto a road which is already close to 100% full. Usually, this forces a car on the road to brake in order to keep the correct distance between cars. Since a speed reduction lowers the road capacity (Figure 3), this can suddenly cause the road to be more than 100% full.[/quote]That is not the main point. Drivers tend to over-react, and brake later and more than necessary.There are many simulations where you can study traffic flow for various different parameters, e.g. http://www.traffic-simulation.de/. Large decelerations increase the risk of a jam.
[QUOTE="Svein, post: 5555196, member: 538805"]Been done. It's called a train.[/QUOTE]Yes, but a train in endless motion which can pick up and drop off cars without stopping.
I'm wondering about the effect that speed has on how many cars there are on a freeway at any moment in time. At higher speeds, a commuter spends less time on the freeway (since the destination / freeway exit is reached sooner), which should result in fewer cars on the freeway at any moment in time.
[QUOTE="anorlunda, post: 5554941, member: 455902"]They say that the only way to do that is automated driverless vehicles that can operate with nearly zero distance between them.[/QUOTE]Been done. It's called a train.
A follow up to my prior post. The key factor is number of cars per unit time. The commuters tend to follow more closely, perhaps 1 car every 2.5 seconds (perhaps as low as 1 car every 2 seconds) versus 1 car every 3 seconds. The higher average speed effect is an indirect factor, as most drivers tend to follow at about the same fixed distance behind other cars for a range of speeds, perhaps from 55 mph / 88 kph to 70 mph / 112 kph, which reduces the time between cars crossing a point, which increases the flow rate.
[QUOTE="rcgldr, post: 5555022, member: 17595"]Seems that article is basing those numbers on distance between cars, rather than time between cars. On southern California freeways, when congestion has not occurred, the morning commuters tend to achieve higher flow rates (number of cars per unit time) then the afternoon combination of commuters, shoppers, … , with the higher flow rates correspond to higher average speed as noted in Svein insight. Other factors like morning commuters tending to follow each other more closely (for example flow rate around 1 car per 2.5 seconds rather than 1 car per 3 seconds), reacting and recovering quicker from temporary slow downs also helps. Once congestion occurs and speeds slow down, the flow rate decreases. This is obvious in the case where the speeds are so slow that the flow rate (per lane) becomes less than 1 car per 3 seconds.[/QUOTE]I have found, purely anecdotally, that traffic flow on the freeways where I live (Seattle area) is better during the weekdays than on the weekends. My explanation for this is in line with your comment, [USER=17595]@rcgldr[/USER], that daily commuters are more tuned into the traffic flow than the weekend drivers, some of whom drive the posted speed limit in the fast lanes.
[QUOTE="Greg Bernhardt, post: 5553999, member: 1"]Here is a comment from Reddit … " urban planners will tell you that streets with slower speed limits actually move more cars."[/QUOTE]Seems that article is basing those numbers on distance between cars, rather than time between cars. On southern California freeways, when congestion has not occurred, the morning commuters tend to achieve higher flow rates (number of cars per unit time) then the afternoon combination of commuters, shoppers, … , with the higher flow rates correspond to higher average speed as noted in Svein insight. Other factors like morning commuters tending to follow each other more closely (for example flow rate around 1 car per 2.5 seconds rather than 1 car per 3 seconds), reacting and recovering quicker from temporary slow downs also helps. Once congestion occurs and speeds slow down, the flow rate decreases. This is obvious in the case where the speeds are so slow that the flow rate (per lane) becomes less than 1 car per 3 seconds.
Fun topic. Well done. I await your follow-up article on the dynamics.I read that freeway designers in Southern California have been told that they must triple capacity in the future with no new roads, no additional lanes. They say that the only way to do that is automated driverless vehicles that can operate with nearly zero distance between them.
Here is a comment from Reddit[QUOTE]This is cute from a physics point of view, but in real life, urban planners will tell you that streets with slower speed limits actually move more cars. A typical chart is on page 10 of this report. So in reality, speed limits do affect capacity, they just affect in the opposite way that you'd think.[/QUOTE]
Definitely clears up a common misconception and I found this more interesting than I ever thought possible. Kudos!!
Very clear and well done. I think traffic engineers use the term saturation for the situation where the road is at or exceeds capacity. And you can have a situation as in your example where periodic stoppages cause "over-staturation", as in: traffic signals, accidents, rubbernecking drivers and so on. Queueing theory works well to explain things then I believe.Your article would make a great addition to traffic school for people learning to drive.