Intro to the Big Bang and Infinity Concepts

In the cosmology section of the Physics Forums, I encountered many Big Bang and related infinity problems. Hence, in this article, I want to explain the Big Bang, the topology of the Universe, and the concepts of singularities and infinities.

First, let’s start with the concept of the observable universe and what we mean by that. The observable universe is the part of the Universe that we can currently see (observe). The observable universe has a finite size and the current radius of the observable universe is approximately 46.6 billion light-years.

As we know, signals that come from distant objects travel at the speed of light. Hence, there’s a limit to what we can see. Since these signals come from all directions, the observable universe can be thought of as a sphere centered on us. (In this sense “center” doesn’t mean that we are at the center of the Universe. The universe and observable universe are different concepts).

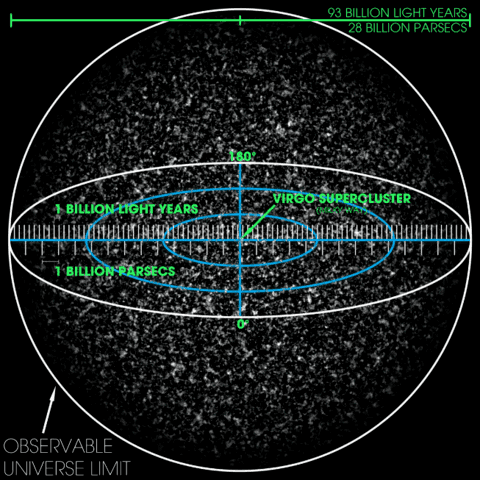
               Fig. 1: The observable universe centered on us ^[1].

The critical point in this concept is that the observable universe would be different for different observers. For example, “the observable universe” for an observer in the Andromeda galaxy would be different than ours.

In this sense, the Universe will mean the Observable Universe plus everything outside of the Observable Universe.

          About the Infinities

As we may expect, the Universe can have two possible sizes depending on its geometry; It can be infinite or finite.

       I. Finite Size Universe

In this case, the Universe can have a spherical, toroidal (torus), or another type of spatial geometry. But there is a very important thing that we should be careful about when we try to imagine such spatial geometry. We usually think of a sphere embedded in a space, and we look at it from the outside and say “Well, that’s the Universe”. This kind of approach is wrong. Since there’s no such thing as an “outside of the Universe”. We can’t imagine the Universe from the outside point of view because as I said before, the Universe encloses everything and anything possible.

In three dimensions, imagining such topology can be challenging hence, the two-dimensional analogy can be used to describe the situation.

An easier way to imagine the concept of the finite universe is, thinking of ourselves as a 2D creature on a two-dimensional positively curved universe (surface of a sphere). Since we are 2D creatures, we can move only in 2 general directions; forward-backward and right-left. On the surface of a sphere that is expanding in the same manner as our universe, if we started at a fixed point in co-moving coordinates and traveled at some faster-than-light speed in any direction along a great circle of the sphere, we could eventually find ourselves back at the point where we started. The idea of finding ourselves in the same place is the main concept of the finite universe. There wouldn’t be any edge for us and we can go on forever and we may find ourselves in the same spot repeatedly.

       II. Infinite Size Universe

In this case, the Universe can have a hyperbolic or flat spatial geometry where the universe goes on forever. Unlike a finite universe, we can go on forever and never come back around to a location we’ve already been.

          About the Big Bang 

Now let’s consider the Big Bang. In this article, I’ll specifically talk about the Big Bang singularity. People who try to explain the Big Bang singularity often say that the universe started from a point and then it evolved. But this description does not reflect the truth. Big Bang singularity cannot be treated as a “point-type explosion”. The problem arises when we think of singularity as a “point in space-time”. But why do we say it didn’t start from a point but still say it started from a singularity? What is the main difference?

According to Einstein’s general theory of relativity, spacetime at every event has definite curvature. If that curvature is everywhere infinite, we define no spacetime at all. If we try to imagine the time of the Big Bang itself as being covered by cosmology, we are saying that there is a time at which spacetime is not properly defined. So, there can be no time in the cosmology corresponding to the Big Bang. We describe the Big Bang as a “singularity”, a breakdown in the laws that govern space and time.

The term singularity, roughly speaking, designates a point in a mathematical structure where a quantity fails to be well defined, even though the quantity is well defined at all neighboring points. The simplest and best-known example arises with the inverse function, $\frac {1} {x}$. As long as $x$ is non-zero, $\frac {1} {x}$ is well defined.

But as we approach zero we started to get different infinities

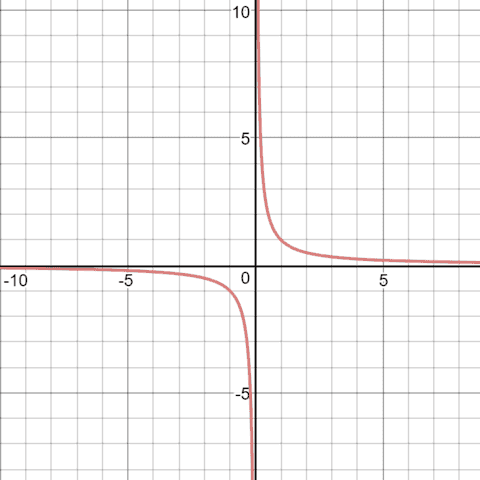
               Fig. 2: The graph of $\frac {1} {x}$

To find the $\lim_{x \rightarrow 0} {\frac {1} {x}}$  we can write,

$\lim_{x \rightarrow 0^-} {\frac {1} {x}}=-∞$

$\lim_{x \rightarrow 0^+} {\frac {1} {x}}=+∞$

As we all know, in arithmetic classes we say that $\frac {1} {0}$ gives us infinity. But that’s not the real case, as we can see a negative value that closes to $0$ can give us minus-infinity, and positive values that close to $0$ give us infinity. So which value should we give for $\frac {1} {0}$? “Plus-infinity” or “minus-infinity”? The safer course is just to say that we have a singularity at $x=0$ and not try to give it any value.

What we can say is this. The Universe has age or time, it’s age after the big bang. The space-time of the Universe exists for every age greater than zero: 1 million years, one hundred years, one second, one-half second, one-tenth second, and so on. No matter how small we make the age, there is a corresponding spacetime, as long as the age is greater than zero. But nothing in general relativity (no spacetime at all) corresponds to the zero-age (similar case of $\frac {1} {0})$.

This moment of zero-age is fictitious in the history of the Universe. In that regard, it is like the fictitious point “at infinity” on the horizon where parallel lines meet. Of course, we all know that there is no such point, although we see it drawn routinely in perspective drawings ^[2].

Now, let me combine these ideas to see the full picture,

In case 1, we are living in an infinite universe, it was infinite at the beginning of the universe (after the big bang) and it’s still infinite.

In case 2, we are living in a finite universe. At the beginning of the universe (just after the Big Bang), the universe was finite, and it will always be finite. This means that when you travel in a certain direction you may find yourself at the same point at which you started the journey.

In both cases, the universe is possibly finite in time, and again in both cases, the universe can expand. Even if the universe is infinite.

          Conclusion

In cosmology, from looking at the CMBR, we can have some ideas about the topology of the universe. In the recent Planck 2015 data, we see that the observable universe has a flat geometry (within the limit of our measurement). It normally implies an infinite size universe, but it doesn’t have to be necessarily true.

For example, think of a two-dimensional positively curved universe (to visualize the concept more easily). We could have been living in an infinitesimal portion of the surface of that sphere, so that, when we try to measure the curvature of the observable universe, we get zero. Hence, in this scenario, we can assume that the universe is infinite (since the portion of the universe that we observed, seems to be flat). But, we know that the universe is finite in size and thus our assumption was wrong.

In this sense, we cannot know the size or the topology of the universe from CMBR data. We can say that the observable universe is flat (again, only to within our ability to measure it).

We model the universe as being infinite, but we know that future measurements may show that it is finite.

In short, the Universe may be finite in time, also our measurements support either an infinite universe or a finite universe whose curvature is so small that we cannot measure it at this time. The Universe expanded from a singularity (not an explosion from a point in space) in an event we call the Big Bang and eventually evolved into the Universe we live in today.

Special thanks to @Drakkith and @phinds who helped me with the editing.

       References

  1- Observable Universe (https://en.wikipedia.org/wiki/Observable_universe)

2- Retrieved from (http://www.pitt.edu/~jdnorton/teaching/HPS_0410/chapters/big_bang_FRW_spacetimes/#What)

       Further Reading

1- The Status of Cosmic Topology after Planck Data (https://arxiv.org/ftp/arxiv/papers/1601/1601.03884.pdf)

2- Planck 2015 results. XVIII. Background geometry & topology (https://arxiv.org/abs/1502.01593)