Exploration into the Physics of Rainbows

For several years, I have been contemplating this beautiful picture by photographer Brian McPhee. I have a personal interest in the photograph because that boat is my year-round home. I also have a scientific interest in the photograph because of what it teaches me about rainbow physics.
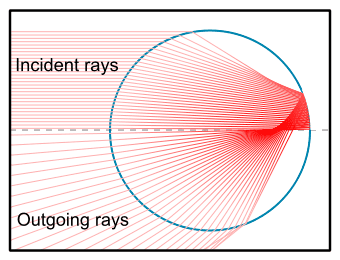
The simplest explanation of rainbow physics is based on internal reflections in the near-spherical shape of a raindrop.
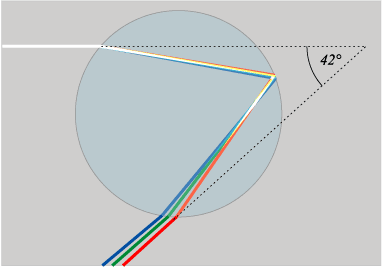
Light rays enter a raindrop from one direction (typically a straight line from the sun), reflect off the back of the raindrop, and fan out as they leave the raindrop. The light leaving the rainbow is spread over a wide-angle, with a maximum intensity at the angles 40.89–42°. (Note: Between 2 and 100% of the light is reflected at each of the three surfaces encountered, depending on the angle of incidence. This diagram only shows the paths relevant to the rainbow.) — See Wikipedia Rainbow or The Theory of the Rainbow (Scientific American 1977)
Look carefully at the photo with the boat. You will see that the sky inside the arc is much brighter than the sky outside the arc. Some scientists claim that no such effect exists, but it’s pretty plain in the picture. The explanation is that raindrops inside the arc reflect sunlight toward me, while drops outside the arc reflect sunlight away from me. The colors appear in the transition region where only certain colors are reflected towards my eye.
More challenging physics comes from the image of the rainbow seen on the surface of the water. At first, I assumed that it was a reflection of the rainbow in the sky, just like reflections of blue sky and white clouds one sees on a calm day in a reflecting pool. But then I came across Can Rainbows Cast Reflections? on the website of noted astronomer Bob Berman. Paraphrasing Berman. “No, they do not. Rainbows are not 3D objects and they do not cast reflections. In the water, you see a different rainbow, not a reflection.” I spent a lot of time puzzling over that, because I didn’t understand Berman’s explanation. I also doubted its truth because I’m sure that I have seen rainbows in the rearview mirror as I drive. It sounds like the Hollywood version of vampires that don’t make reflections in mirrors.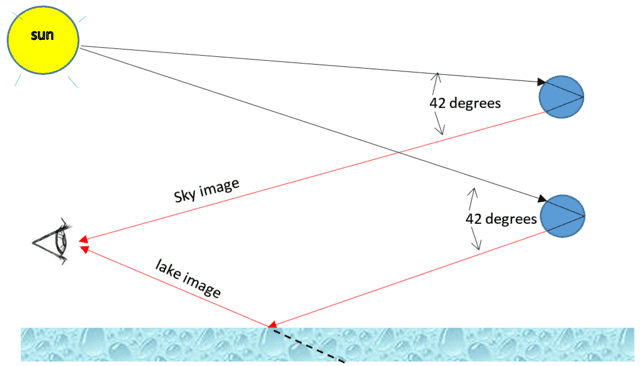

At first, I thought that Berman meant that the image in the water was sunlight hitting the surface and creating a rainbow effect as it was refracted back to my eye. But no, that won’t work because the water in the lake is not in the form of spherical droplets.
After much thinking, I think I’ve got it. No vampire magic is required. The colored light you see from a rainbow is not omnidirectional, it is a unidirectional beam aimed at your eye. By analogy, imagine a man at the far end of a hall of mirrors holding a laser pointer pointed at your eye (assume a laser suitably attenuated for safety). The mirrors on the walls, ceiling, and floor of this hall will show many images of the man, but they will not show the red dot of the laser because the laser beam doesn’t hit those mirrors. However, if you turn your back, step to the side, and hold up a rearview mirror, you’ll see both the man and the red dot. That is because the rearview mirror is inside the cone of light from the laser pointer. So, to say that the red dot (or the rainbow) does reflect and that it does not reflect are both true statements depending on which mirror it refers to. Yet, the image of the man appears in all the mirrors. The man is a 3D object, but the red dot is not.
So, what do we see on the surface of the lake in the picture? That image is below the horizon from the eye of the camera. It is reflected light. It does pass through raindrops first, but not the same raindrops as the ones creating the sky image.
This diagram illustrates, [except for the important fact that light rays from the sun are actually parallel]. The image seen in the sky comes from different raindrops than the image seen reflected in the lake. In fact, the reflected image appears to be below the horizon (dotted line). In that sense, it is true that the image seen on the lake surface is not a reflection of the rainbow seen in the sky. It is a reflection of a different rainbow.
Using the same logic, it is correct to say that nobody else can see the same rainbow that I do. As I stand, a person sitting near me sees light reflected from different raindrops than I do. And if we consider light reaching me and him from the same raindrop, I might see green light while he sees red. That is because of the difference in angles between the drop, my eye, and his eye. In that sense, his rainbow is not the same as mine.
I was going to end this article here, but PF mentor jedishrfu urged me to continue with other rainbow effects, so I will. One of Wikipedia’s very best articles, Rainbow, is a rich source.
Table of Contents
Double, Triple, Quadruple, and Quintuple Rainbows
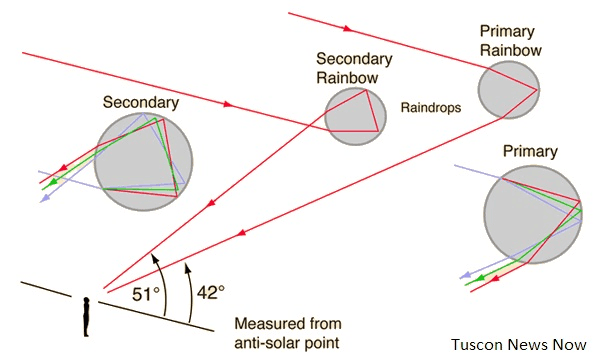
The primary rainbow is reflected once inside the raindrop. It is possible to have 2, 3, 4, or 5 reflections before the beam exits the drop. Of course, higher-order rainbows are dimmer and thus harder to see. (Picture source Tuscon News Now.)
Most of you have probably seen a double rainbow in real life. People living close to the arctic circle have probably seen triple rainbows.
If you see higher-order rainbows, they are always outside and concentric from the primary rainbow. If the order of colors in the odd-numbered rainbows is ROYGBIV, then the order in the even-numbered rainbows is VIBGYOR.
Twinned Rainbow
Let me make an assertion. To see a rainbow, many or most of the raindrops must be of uniform size and shape. My argument for that is that drop size and shape are related. As the drops fall, air resistance flattens small drops more than large drops. Flattened drops reflect at a different angle. Flattened drops might also oscillate or tumble. If the statistics of the raindrops are diverse, then the light will be reflected in many directions other than toward your eye, so you won’t see a rainbow. If you do see a rainbow, that is direct evidence of the uniformity or correlation of the drop statistics.
A twinned rainbow happens when there are two predominant drop sizes. The small flattened drops reflect at a different angle than the larger drops.
Circular Rainbows
A rainbow is usually seen as less than half a circle. In the right circumstances, full-circle rainbows can be seen above you in the sky, or below when you view from high up. However, physics is the
same.
Contrary to my prior beliefs, I learned that full circle rainbows are not the same physics as a glory or a 22° halo.
Wikipedia says that the glory is believed to happen due to classical wave tunneling, when light nearby a droplet tunnels through the air inside the droplet and are emitted backward due to resonance effects. (Picture Brocken Inaglory)

The 22° halo is due to reflections in ice crystals that are hexagonal, not spherical. (Picture Gladson Machado)
Sun dogs are closely related. The image below shows very bright sun dogs in Fargo, North Dakota. Also visible are parts of the 22° halo (the arcs passing through each sundog), a sun pillar (the vertical line), and the parhelic circle (the horizontal line).


Supernumerary Rainbow
A supernumerary rainbow—also known as a stacker rainbow—is an infrequent phenomenon, consisting of several faint rainbows on the inner side of the primary rainbow, and very rarely also outside the secondary rainbow. Supernumerary rainbows are slightly detached and have pastel color bands that do not fit the usual pattern.
It is not possible to explain their existence using classical geometric optics. The alternating faint rainbows are caused by interference between rays of light following slightly different paths with slightly varying lengths within the raindrops.
The very existence of supernumerary rainbows was historically a first indication of the wave nature of light, and the first explanation was provided by Thomas Young in 1804 — Wikipedia Rainbow
A supernumerary rainbow picture by Andrew Dunn
Reflected and Reflection Rainbows
The picture of the boat shows a reflected rainbow. We already discussed the physics of that.
A reflection rainbow is seen when the sunlight is reflected from the water surface first, then up to raindrops in the sky, then internally reflected by raindrops back toward your eye.
Monochrome Rainbows
When the sunlight is red, such as at dawn or dusk, then rainbows can still be formed but they will be monochrome. (Image by www.rodjonesphotography.co.uk)
When rainbows are formed by moonlight, they appear to be the
same white color as The Moon. Fogbows also appear to be mostly monochromatic. Fogbows are formed by the same physics as rainbows, but they are made with much smaller drops closer to the horizon.
Someday (probably well beyond my lifetime) we could have a close passage by a large comet with a brilliant tail. If that happens, rainbows could be formed with comet light. They would show us the spectrum of the comet’s light source, monochromatic or not.
Could we see a rainbow formed by the light from an aurora in the stratosphere? That sounds difficult (because the aurora is not a point source) but not quite impossible. That is fun speculation. Maybe someone could finance a year for me in Iceland so that I could research that.
Mystery Rainbow
This remarkable picture, by dabrandner, appears to show a
third rainbow sandwiched between the primary and secondary double rainbows. I call it a mystery because I’m not sure if the third rainbow is a twinned rainbow or a reflection rainbow, or some other kind. [Reader comments are welcome.]

Conclusions
I confess that when I started this article with just a picture of my boat, I had no idea how far my research would take me into interesting physics phenomena. Thank you jedishrfu for egging me on.
Using the sky as a scientific instrument, we can observe:
- How light behaves inside the raindrops.
- The reflection behavior of unidirectional versus omnidirectional light beams.
- The statistical distribution of drop size and shape.
- Some quantum effects (Superluminary)
- Evanescent wave coupling, an exotic field of optics I never heard of before.
- A spectrograph of the light source.
- Science history from 1804.
I’m sure you will agree, that is very cool.
Thanks to jedishrfu and to Greg Bernhardt for their assistance and encouragement.
Dick Mills is a retired analytical power engineer. Power plant training simulators, power system analysis software, fault-tree analysis, nuclear fuel management, process optimization, power grid operations, and the integration of energy markets into operation software, were his fields. All those things were analytical. None of them were hands-on.
Dick has also been an exterminator, a fire fighter, an airplane and glider pilot, a carney, and an active toastmaster.
During the years 2005-2017. Dick lived and cruised full-time aboard the sailing vessel Tarwathie (see my avatar picture). That was very hands on. During that time, Dick became a student of Leonard Susskind and a physics buff. Dick’s blog (no longer active) is at dickandlibby.blogspot.com, there are more than 2700 articles on that blog relating the the cruising life.










[QUOTE=”sophiecentaur, post: 5343690, member: 199289″]… You can see a rainbow ‘against’ the dark ground in front of you but that doesn’t mean the image is that close. Your brain does its best to place it in space …
[/quote]
This is really confusing. The rainbow here is definitely between me and the guy in the black t-shirt. But the image [B]isn’t[/B]?
[ATTACH=full]94267[/ATTACH]
Scratches head for 10 minutes…..
Ok. I think I understand both viewpoints now.
The raindrops are just acting like a bazillion, somewhat complicated little mirrors.
We could replace them with much larger standard mirrors, such that they all reflected the sun at you.
Then it would be obvious that the images you were seeing, were in fact, the sun.
But then…….
We could argue that the guy with the rainbow shorts is just a bazillion little atoms, which are not very good mirrors, in any sense of the word.
But he does reflect sunlight, and we don’t call him a reflection of the sun.
So I’m going to go back and agree with anorlunda, that we are arguing semantics, rather than science.
[quote] …
This conversation is fizzling out now – like a damp firework – everything has been said except the ray diagram of the light paths above the ground showing how that inverted bow is formed. I can sort of go along with your mirror image idea; it certainly ought to be right.
There was an issue about spurious rainbows that don’t fall on the expected cone (s) but the particular circumstances would need to be quoted; for instance, there could be a strong ray of reflected sunlight and that could produce its own bow.[/QUOTE]
Well, it may be fizzling, but it’s generated a few new questions in my brain. Unfortunately, I think it would take me a week to figure out how to ask the questions, such that people could understand what I was asking.
Ever since I caught the image of my rainbows intersecting at ≈90°,
[CENTER][IMG]http://www.europa.com/~garry/rightanglerainbows.jpg[/IMG] [/CENTER]
I’ve been curious if I could position mirrors to create a complex rainbow image of Mickey Mouse.
Might be impossible. Maybe not impossible. Looking forward to summer. :smile:
Perhaps I’ll study up on optics, and do some maths first.
[QUOTE=”spareine, post: 5342943, member: 351563″]In an old PF-thread, ‘Drove through the rainbow’,[[URL=’https://www.physicsforums.com/threads/drove-through-a-rainbow.100103/#post-3522536′]1[/URL]] your were the proponent of the view that a rainbow is not the raindrops and not the cone, but a virtual image at infinity, even behind a hill, because it follows from parallax and geometrical optics. I am still wondering why you are so hesitant about that view in this thread.[/QUOTE]
I don’t see any inconsistency there. The thing that generates an image can be anywhere and so can the image. You don’t see the drops and you can’t see the cone (shape) because you are looking along it from the vertex. All you see is an image that is a long way away (parallax). I don’t think I have changed my view at all. You can see a rainbow ‘against’ the dark ground in front of you but that doesn’t mean the image is that close. Your brain does its best to place it in space and the cues point to the ground, even when parallax is telling you otherwise, because the bow appears (to me at least) to be moving over the ground as I move.
This conversation is fizzling out now – like a damp firework – everything has been said except the ray diagram of the light paths above the ground showing how that inverted bow is formed. I can sort of go along with your mirror image idea; it certainly ought to be right.
There was an issue about spurious rainbows that don’t fall on the expected cone (s) but the particular circumstances would need to be quoted; for instance, there could be a strong ray of reflected sunlight and that could produce its own bow.
In an old PF-thread, ‘Drove through the rainbow’,[[URL=’https://www.physicsforums.com/threads/drove-through-a-rainbow.100103/#post-3522536′]1[/URL]] your were the proponent of the view that a rainbow is not the raindrops and not the cone, but a virtual image at infinity, even behind a hill, because it follows from parallax and geometrical optics. I am still wondering why you are so hesitant about that view in this thread.
[USER=351563]@spareine[/USER]
I think I am getting this now. I struggled a bit to find exactly what your unconventional diagram was getting at but the mirror image approach does make some sense. I would still like to see what goes on above the lake’s surface in a bit more detail (3D) than in my diagram.
[QUOTE=”sophiecentaur, post: 5342539, member: 199289″]But the Sun needs to be shining – or you need a very bright light source at some (∞) distance.[/QUOTE]
So? This is always the case – you need a primary object and the necessary optical setup in order to have a visual virtual object. Here we are talking about a virtual image of the Sun and so naturally the Sun needs to be shining. If it does not or if the necessary optical setup (raindrops + proper line of sight) is missing, you will not see a rainbow. If you do not have a source or if you do not have a mirror, you will not see a virtual image of the source in a mirror.
Edit: All the post you replied to was saying was that you did not have to wait for the correct optical setup (i.e., raindrops). Of course you still need the source, but the optics you can add manually (given line of sight …).
[QUOTE=”Buckleymanor, post: 5342368, member: 181527″]You don’t have to arrange the rain to come at the right time of the day and month you could make a spray with some with water and a hose.[/QUOTE]
But the Sun needs to be shining – or you need a very bright light source at some (∞) distance.
[QUOTE=”anorlunda, post: 5342449, member: 455902″]If two people look through different mirrors, they see the same color object. If two people see light from the same drop at different angles, they see different colors.[/QUOTE]
Yes, but this is not the issue. If two people look through a mirror, the light from a given object is reflected at different parts of the mirror too. The question is not which raindrop reflected what – the question is where the virtual object is and the answer to that is “in the celestial sky”. There is no difference to the mirror case here, if you remove the part of the mirror one person sees an object through, the person will not see it and if you remove the raindrops a person sees the rainbow through the rainbow will disappear.
The raindrops are not where the virtual image is.
[QUOTE=”anorlunda, post: 5342449, member: 455902″]I still think we are just debating semantics. The “object” in question to an optics expert is the sun, but the common language meaning of “I see a rainbow” is that people think of the rainbow as the object. They may not be optically correct, but that is what they mean by the word rainbow.[/QUOTE]
They would be perfectly optically correct. The rainbow is a virtual object in the celestial sky. You just need certain conditions to be fulfilled in order to see this virtual object – just as you need a mirror present to see a mirror image.
Just semantics? Using the rainbow circle it was easy predict the shape and location of the reflected rainbow and the reflection rainbow in this thread, and the prediction was confirmed by a photo. So far attempts failed to predict the same using the rainbow cone.
[QUOTE=”Orodruin, post: 5342218, member: 510075″]The point that there are different raindrops causing the rainbow for different observers is a point well taken. But I do not think this is very different from two people looking at the same object through different mirrors[/QUOTE]
If two people look through different mirrors, they see the same color object. If two people see light from the same drop at different angles, they see different colors.
I still think we are just debating semantics. The “object” in question to an optics expert is the sun, but the common language meaning of “I see a rainbow” is that people think of the rainbow as the object. They may not be optically correct, but that is what they mean by the word rainbow.
[QUOTE=”Buckleymanor, post: 5342368, member: 181527″]You don’t have to arrange the rain to come at the right time of the day and month you could make a spray with some with water and a hose.[/QUOTE]
That’s how I make them.
[QUOTE=”Buckleymanor, post: 5342371, member: 181527″]I am not sure if they are not 3D objects.
[/quote]
Ha ha! The semantics of science. The two “nots” cancel and your phrase becomes; “I am sure if they are 3D objects”.
Which, if you throw out the “if”, looks suspiciously like “I am sure they are 3D objects”.
I suspect they are 3D objects.
Where the hell is [USER=4]@Janus[/USER] when you need a ray-trace guru!?!?!?
[quote]If you stood in the same position and took a series of photos of the rainbow would the rainbow appear as a sphere when the photos were combined together.Provided there was enough time to do it.[/QUOTE]
Now that sounds like a grand experiment!
ps. Rainbows are complicated. I like that about them. :smile:
[QUOTE=”sophiecentaur, post: 5342351, member: 199289″]Why do you have the sun coming off-axis in your diagram, I wonder?
That photo is impressive but it shows the secondary bow being symmetrical about the horizontal*. In your diagram, the secondary bow would appear to include point C, which is not symmetrical about the horizon. Your diagram isn’t clear about how (if) the image in direction AC ever appears as an image in direction of B’. [/QUOTE]
May be this helps: the proportions in my diagram are misleading. The rainbow circle is infinitely far away, whereas the size of the water is finite. The red rainbow B is centered at the antisolar point C. The green reflected rainbow B’ is centered at the the reflected antisolar point C’. Bow B and bow B’ are mirror images with respect to the celestial horizon. (Bow B’ is a curve, it doesn’t ‘include’ point C. I am not sure what is meant by an image in direction AC; C is the antisolar point)
[QUOTE=”sophiecentaur, post: 5342351, member: 199289″]I think the inverted bow in the photograph is formed by droplets above the lake surface and rays from the sun that are reflected by the the lake and then by low level droplets. That would account for the symmetry.
I wouldn’t call my diagram a ‘reflected’ rainbow – it isn’t formed by the same raindrops as the main bow and it isn’t a ‘reflection’ of the main bow. In fact, it there were only a shallow layer of drops in the air, the ‘reflection’ bow would be formed but the main one wouldn’t.
There is some doubt about your explanation and it would help to resolve it if you could quote another source / reference.[/QUOTE]
In your diagram and my diagram the light ray reflects at the water surface between the raindrop and the eye. Therefore it is part of the reflect[U]ed[/U] rainbow. The reflected rainbow circle and the reflection rainbow circle are part of the same celestial circle (42º around C’ ). However they rarely occur simultaneously.
[QUOTE=”sophiecentaur, post: 5342351, member: 199289″]Why do you have the sun coming off-axis in your diagram, I wonder?[/QUOTE]
You can have a rainbow without having dusk or dawn, but yes, the cone axis should be aligned with the incoming sunlight. The center of the circle on the celestial sphere is going to be antipodal to the sun and therefore generally below the horizon. This is also why the mirror image of this circle looks like it does in the attached photo.
[QUOTE=”sophiecentaur, post: 5342351, member: 199289″]I wouldn’t call my diagram a ‘reflected’ rainbow – it isn’t formed by the same raindrops as the main bow and it isn’t a ‘reflection’ of the main bow.[/QUOTE]
Yes it is! Even if it has not passed through the same drops. The image is on the celestial sphere, not at the raindrops. This is also crucial for understanding why it appears reflected in the lake in the photo. The rays AC and A’B’ both extend to the same point on the celestial sphere, since they are parallel.
[QUOTE=”spareine, post: 5338924, member: 351563″]I agree that rainbows are not 3D objects. Our difference is simply that I prefer to extrapolate the light rays back to infinity. For me raindrops are merely mirror particles at a finite distance, they are certainly not the location of the rainbow. Extrapolate the light rays back to infinity to find the virtual object. The celestial sky is the location of the rainbow. Everybody sees the rainbow at the same location in the celestial sky.[/QUOTE]
I am not sure if they are not 3D objects.If you stood in the same position and took a series of photos of the rainbow would the rainbow appear as a sphere when the photos were combined together.Provided there was enough time to do it.
[QUOTE=”sophiecentaur, post: 5338934, member: 199289″]The imaging forming structure in a rainbow is different from what happens in a lens – it’s more like a multiplicity of lenses, with each lens contributing within a narrow angle. It’s a bit like what happens with a lenticular screen or a fresnel lens. I think it’s a bit pointless to try to make the rainbow fit in with the more straightforward images that we see. Of course the image is not ‘real’ because the light behaves as if it comes from way behind the image forming structure. There is no parallax against distant objects so it can be classed as infinitely far away.
I don’t think they do, exactly. The distances are so large that it would be difficult to spot but when you move to the left, the bow moves to the left, with you. So it would be moving across the sky relative to the distant stars. The centre of the bow is in line with the Sun and the back of your head. But a rainbow at night? Weird idea! Perhaps it’s an experiment you could do with the Moon – if you could arrange the rain to come at the right time of the day and month. But you would need to travel quite a distance sideways to see the effect against the moonscape as a background. (many km to observe a recognisable movement of a fuzzy thing like a rainbow.[/QUOTE]
You don’t have to arrange the rain to come at the right time of the day and month you could make a spray with some with water and a hose.
[QUOTE=”spareine, post: 5342276, member: 351563″]No need to be afraid, a flat mirror is basic geometrical optics. Rays from the raindrops contributing to the reflected rainbow could be extrapolated to A’. And there is photo evidence like [URL=’http://www.mallucafe.com/pic/3331-a-beautiful-reflection-of-rainbow-in-dal-lake-kashmir-india’][U][COLOR=#0066cc]this[/COLOR][/U][/URL].
[ATTACH=full]94219[/ATTACH]
(About reflected/reflection rainbow: your diagram seems to be about the reflect[U]ed[/U] rainbow. The picture of the boat shows a reflected rainbow, as anorlunda said. A reflect[U]ion[/U] rainbow is a rare phenomenon seen in the sky.)[/QUOTE]
Why do you have the sun coming off-axis in your diagram, I wonder?
That photo is impressive but it shows the secondary bow being symmetrical about the horizontal*. In your diagram, the secondary bow would appear to include point C, which is not symmetrical about the horizon. Your diagram isn’t clear about how (if) the image in direction AC ever appears as an image in direction of B’. I think the inverted bow in the photograph is formed by droplets above the lake surface and rays from the sun that are reflected by the the lake and then by low level droplets. That would account for the symmetry.
I wouldn’t call my diagram a ‘reflected’ rainbow – it isn’t formed by the same raindrops as the main bow and it isn’t a ‘reflection’ of the main bow. In fact, it there were only a shallow layer of drops in the air, the ‘reflection’ bow would be formed but the main one wouldn’t.
There is some doubt about your explanation and it would help to resolve it if you could quote another source / reference.
*Notice the apparent vignetting in that picture too.
[QUOTE=”sophiecentaur, post: 5342178, member: 199289″]You will have to give a[I] reference or derivation[/I] of that, I’m afraid. Whilst we can see part of the rainbow proper ‘in the surface’ of the lake, the drops producing that are between the surface of the water and your eye (just the same as when we see rainbows against the grass in a field. I tried to decide how the reflection rainbow (not ‘reflected rainbow’) would be formed and the 3D geometry needed to describe what happens in a spherical droplet, off axis, is hard. But I can’t see how any of this can explain the horizontal spectrum that’s shown in the ‘boat picture’ without a formal ray tracing calculation. My diagram in post 26 shows how the bow must appear below and closer to the horizon – but can it really be that near to the horizon?[/QUOTE]
No need to be afraid, a flat mirror is basic geometrical optics. Rays from the raindrops contributing to the reflected rainbow could be extrapolated to A’. And there is photo evidence like [URL=’http://www.mallucafe.com/pic/3331-a-beautiful-reflection-of-rainbow-in-dal-lake-kashmir-india’][U][COLOR=#0066cc]this[/COLOR][/U][/URL].
[ATTACH=full]94219[/ATTACH]
(About reflected/reflection rainbow: your diagram seems to be about the reflect[U]ed[/U] rainbow. The picture of the boat shows a reflected rainbow, as anorlunda said. A reflect[U]ion[/U] rainbow is a rare phenomenon seen in the sky.)
[QUOTE=”sophiecentaur, post: 5342178, member: 199289″]Anorlunda’s point is totally valid because you have to ask yourself which group of raindrops are you using.[/QUOTE]
The point that there are different raindrops causing the rainbow for different observers is a point well taken. But I do not think this is very different from two people looking at the same object through different mirrors. I would still call it the same object and if one of the mirrors disappear, one person will not see the object.
[QUOTE=”sophiecentaur, post: 5342178, member: 199289″]My diagram in post 26 shows how the bow must appear below and closer to the horizon – but can it really be that near to the horizon?[/QUOTE]
If you are talking about where the drops are which make the reflection, this is not true. It depends on how far away they are. The rainbow on the celestial sky as mentioned by spareine is a more useful concept and for that it the the same (virtual) image at infinity which is relevant (which is then also reflected in the lake). As to where the raindrops are which make you see this image, they are all in a cone and (for the reflected image) in the reflection of that cone in the water surface.
[QUOTE=”spareine, post: 5342143, member: 351563″][COLOR=#0000ff]Instead of calling someone insane,[/COLOR] we could verbalize a distinction to avoid confusion: for some people rainbow means the ‘rainbow cone’ within the shower, for others it means the ‘rainbow circle’ in the celestial sky. Then:
– two persons see the same rainbow circle, but different rainbow cones.
– Through the water surface a reflected-rainbow circle can be seen, it is another circle in the celestial sky.
– the reflected-rainbow cone and the rainbow cone are not the same cones.[/QUOTE]
Calm down, dear boy. No one really believes that you’re mad (no worse than the rest of us, at least). It really is just a way of looking at this, whether you say we all have our own rainbow or we ‘share one’. Anorlunda’s point is totally valid because you have to ask yourself which group of raindrops are you using. Is it the same as my group of raindrops? If we both happen to be looking at a few ‘common’ raindrops then you are seeing a different colour from the colour I am seeing. Either we all have our own rainbow or we alll share the same one. (Does anybody care?)
[QUOTE=”spareine, post: 5342143, member: 351563″]- Through the water surface a reflected-rainbow circle can be seen, [COLOR=#0000ff]it is another circle in the celestial sky.[/COLOR][/QUOTE]
You will have to give a[I] reference or derivation[/I] of that, I’m afraid. Whilst we can see part of the rainbow proper ‘in the surface’ of the lake, the drops producing that are between the surface of the water and your eye (just the same as when we see rainbows against the grass in a field. I tried to decide how the reflection rainbow (not ‘reflected rainbow’) would be formed and the 3D geometry needed to describe what happens in a spherical droplet, off axis, is hard. But I can’t see how any of this can explain the horizontal spectrum that’s shown in the ‘boat picture’ without a formal ray tracing calculation. My diagram in post 26 shows how the bow must appear below and closer to the horizon – but can it really be that near to the horizon?
I am not the one who ordinarily thinks of the rainbow as a cone, so that is not my problem.
[QUOTE=”spareine, post: 5342143, member: 351563″]Instead of calling someone insane, we could verbalize a distinction to avoid confusion: for some people rainbow means the ‘rainbow cone’ within the shower, for others it means the ‘rainbow circle’ in the celestial sky. Then:
– two persons see the same rainbow circle, but different rainbow cones.
– Through the water surface a reflected-rainbow circle can be seen, it is another circle in the celestial sky.
– the reflected-rainbow cone and the rainbow cone are not the same cones.[/QUOTE]
In semantics it takes more than verbalizing a distinction. You have to make the verbalization so wide spread that it becomes part of the language. The man in the street look up and says, “Look, two rainbows.” You reply, “No, two,light cones for one rainbow.” Lots of luck with that.
[QUOTE=”anorlunda, post: 5341299, member: 455902″]But no sane person would argue that these are the same rainbows. [/QUOTE]
Instead of calling someone insane, we could verbalize a distinction to avoid confusion: for some people rainbow means the ‘rainbow cone’ within the shower, for others it means the ‘rainbow circle’ in the celestial sky. Then:
– two persons see the same rainbow circle, but different rainbow cones.
– Through the water surface a reflected-rainbow circle can be seen, it is another circle in the celestial sky. Its center is the mirror image of the antisolar point.
– the reflected-rainbow cone and the rainbow cone are not the same cones.
[QUOTE=”spareine, post: 5338523, member: 351563″]Why denying virtual objects?[/QUOTE]
I just realized that we are wasting effort debating semantics instead of science. Think of one person in New York viewing a rainbow, and another person in Chicago viewing a rainbow. Spareine would argue that both are looking at a virtual image of the sun. But no sane person would argue that these are the same rainbows.
The Insights article said that the sky and lake views are of different rainbows, not different images.
So if two people side-by-side look at the sky, they see light reflected from different raindrops. Are they looking at the same rainbow or different rainbows? I think that’s a matter of semantics, not science.
Reflected rainbow – alternative diagram.
I was trying to make sense of the diagram in the insight article and I realised what my problem was. All light rays from the Sun arrives from the same angle, for an observer on Earth. I tried an alternative diagram which includes this fact (attached). The vertical scale is exaggerated, of course. Exactly how this explains the horizontal shape of the reflection rainbow is not clear. I guess it must be to do with the reflection at low angles of incidence being less than at a glancing angle, so the bow does not form close to the observer.
[ATTACH=full]94162[/ATTACH]
Also, regarding the very pretty image of that lovely boat under a rainbow, it is possible that there’s some vignetting going on around the edges. It’s a common enough effect in pictures of the sky. Is this bright centre a particularly common effect when shooting away from a low sun?
Two objections against considering the rainbow as a virtual object at infinity might be: rainbows appear to be unfocusable, and infinity does not exist in real space. However, rainbows are focusable, because if the Sun was a point-like source of light, sharp Fraunhofer lines would show up in the rainbow [I]only[/I] if the camera lens was focused at infinity. And about infinity: the celestial sky becomes part of real space when defined as the surface of the geocentric sphere beyond which the diurnal parallax is less than an arbitrary detection threshold x.
[QUOTE=”Orodruin, post: 5339266, member: 510075″]No, the [I]virtual[/I] image is behind you, but the light is coming from in front of you. There is nothing strange here, it happens with lenses too.[/QUOTE]
When I was learning about mirrors, lenses and images in School, we used to use long optical pins on a board and established the position of an image using parallax. What you are suggesting is that a similar method would place the image behind me? That is hard to square with my (beware!!!!!) intuition because I couldn’t actually do this with pins on one side and an image on the other. I guess your point is that the Sums place the image behind me. Of course, the rainbow is so diffuse that one can’t actually ‘focus’ on it for an extra clue about its distance.
[QUOTE=”sophiecentaur, post: 5338992, member: 199289″]This doesn’t make sense to me because the image is in front of me whilst the Sun is behind me. Can you explain it please?[/QUOTE]
No, the [I]virtual[/I] image is behind you, but the light is coming from in front of you. There is nothing strange here, it happens with lenses too.
[QUOTE=”Orodruin, post: 5338968, member: 510075″]Technically, the virtual image of the sun which is the rainbow is not located at infinity, but in the [I]same plane[/I] as the sun[/QUOTE]
This doesn’t make sense to me because the image is in front of me whilst the Sun is behind me. Can you explain it please?
[QUOTE=”spareine, post: 5338952, member: 351563″]It is pure geometry. The Sun’s celestial location is the same for everybody, at a given time. Hence the celestial locations of the antisolar point and the 42° circle around it are the same for everybody.[/QUOTE]
Well, this is not strictly true. The difference is an angle of the distance between the people (measured orthogonal to the solar direction) divided by 1 AU. Miniscule and not noticable by eye, but it is there.
Technically, the virtual image of the sun which is the rainbow is not located at infinity, but in the same plane as the sun (although you need to look away from the sun to see it. Just as the sun, the rainbow will be in a very different place wrt the celestial sky in january compared to july.
[QUOTE=”spareine, post: 5338952, member: 351563″]It is pure geometry. The Sun’s celestial location is the same for everybody, at a given time. Hence the celestial locations of the antisolar point and the 42° circle around it are the same for everybody.[/QUOTE]
You are saying that the angle subtended by the Earth from the Sun is negligible. Yes, that sounds reasonable. But how does that relate to the fact that a rainbow moves against the Earth as you move? Ah – it moves by the [I]distance[/I] you move, which means the apparent change in angle against the celestial sphere is zero.
[QUOTE=”sophiecentaur, post: 5338934, member: 199289″]I don’t think they do, exactly.[/QUOTE]
It is pure geometry. The Sun’s celestial location is the same for everybody, at a given time. Hence the celestial locations of the antisolar point and the 42° circle around it are the same for everybody.
[QUOTE=”Orodruin, post: 5338868, member: 510075″]When you construct virtual images of objects using lenses, the rays take different paths as well, passing through different parts of the lens.[/QUOTE]
The imaging forming structure in a rainbow is different from what happens in a lens – it’s more like a multiplicity of lenses, with each lens contributing within a narrow angle. It’s a bit like what happens with a lenticular screen or a fresnel lens. I think it’s a bit pointless to try to make the rainbow fit in with the more straightforward images that we see. Of course the image is not ‘real’ because the light behaves as if it comes from way behind the image forming structure. There is no parallax against distant objects so it can be classed as infinitely far away.
[QUOTE=”spareine, post: 5338924, member: 351563″]Everybody sees the rainbow at the same location in the celestial sky.[/QUOTE]
I don’t think they do, exactly. The distances are so large that it would be difficult to spot but when you move to the left, the bow moves to the left, with you. So it would be moving across the sky relative to the distant stars. The centre of the bow is in line with the Sun and the back of your head. But a rainbow at night? Weird idea! Perhaps it’s an experiment you could do with the Moon – if you could arrange the rain to come at the right time of the day and month. But you would need to travel quite a distance sideways to see the effect against the moonscape as a background. (many km to observe a recognisable movement of a fuzzy thing like a rainbow.
[QUOTE=”anorlunda, post: 5338681, member: 455902″]I think you missed the point, as astronomer Berman said, “Rainbows are not 3D objects.” I too struggled with what that means.[/QUOTE]
I agree that rainbows are not 3D objects. Our difference is simply that I prefer to extrapolate the light rays back to infinity. For me raindrops are merely mirror particles at a finite distance, they are certainly not the location of the rainbow. Extrapolate the light rays back to infinity to find the virtual object. The celestial sky is the location of the rainbow. Everybody sees the rainbow at the same location in the celestial sky.
[QUOTE=”anorlunda, post: 5338750, member: 455902″]A big difference. Zero photons from the laser reach the other eye, with our without your hand.[/QUOTE]
But in the case of the rainbow you are making a virtual image of the sun at infinity. Even if the different rays from this virtual image passes through different rain drops, it does not make them part of a different virtual image. When you construct virtual images of objects using lenses, the rays take different paths as well, passing through different parts of the lens. The important thing is that a virtual image is constructed. It [I]is[/I] this virtual image which is reflected. Fine, the rays did not pass through the same rain drops, but the virtual image is not where the raindrops are.
[QUOTE=”anorlunda, post: 5338681, member: 455902″]Now suppose that the rain just began so that the high drop is there but there is no low drop[/QUOTE]
You could likely get similar effects with the virtual images created by lenses by placing a mirror beyond the lens, clearly the virtual image is not going to be reflected.
[QUOTE=”sophiecentaur, post: 5338745, member: 199289″]I can hold my hand in front of me so that I can see an object with one eye but not the other. Is there any (relevant) difference[/QUOTE]
A big difference. Zero photons from the laser reach the other eye, with our without your hand.
[QUOTE=”anorlunda, post: 5338738, member: 455902″]Because light reflected from an ordinary object goes in many directions. It is (at least partially) omnidirectional light.
Collimated light is unidirectional. A collimated beam can be aimed at your left eye and 0% of its light reaches your right eye.
So a man holding a paper with a red dot printed on it, is very different from a man holding a red laser pointer.[/QUOTE]
I can hold my hand in front of me so that I can see an object with one eye but not the other. Is there any (relevant) difference. Colimation is a way over the top requirement for this explanation. Speaking as one who did all the basic Physics learning in the absence of handy laser pointers, I often find that people reach for a virtual laser to prove points when simple shadows can do just as well. What did the 19th century opticians do when they wanted to explain things?
[QUOTE=”sophiecentaur, post: 5338727, member: 199289″]I don’t wee why it has to be a laser beam.[/QUOTE]
Because light reflected from an ordinary object goes in many directions. It is (at least partially) omnidirectional light.
Collimated light is unidirectional. A collimated beam can be aimed at your left eye and 0% of its light reaches your right eye.
So a man holding a paper with a red dot printed on it, is very different from a man holding a red laser pointer.
One way to think of a rainbow is that it is just a highly distorted virtual image of the Sun. There is a large amount of Chromatic aberration and there is also a lot of spatial distortion – so much so that we see the image as a ring. Because of the apparent direction of arrival of the sections of the bow, there is no parallax so the image appears at infinity. All very confusing and not like other things we see in the sky.
[QUOTE=”spareine, post: 5338523, member: 351563″]Maybe it is useful to add that your statement that two persons cannot see the same rainbow is a denial of the concept of virtual objects.[/QUOTE]
I am sure that, if rainbows didn’t look so gorgeous, they wouldn’t have got into folk lore and they wouldn’t have that extra magical quality that seems to make people treat them differently from other optical phenomena.
I am not being Mr Grumpy about this. I am just suggesting that our intuition is not the best way to attempt descriptions and explanations of rainbows. People are really bad witnesses when asked to describe what they actually see; they seems to believe that the bow actually goes into the ground, for instance. Fact is that, very often, you can actually see a hint of rainbow in front of the ground. (Paradoxical if you want to place the rainbow ‘somewhere’ but no more so than looking at an image in {behind} a mirror).
[QUOTE=”anorlunda, post: 5338681, member: 455902″]The point may be clearer if we refer back to the article’s analogy with a man pointing a perfectly collimated laser at my eye.[/QUOTE]
I don’t wee why it has to be a laser beam. The same thing would apply to any object that happens to be obscured from one viewer and visible to the other. One observer is aware of the object and the other is not.
And, for an object / image to be “3D’ there has to be a spread of distances from the observer to different parts of the object and parallax effects should also be seen. It’s all at infinity so that hardly applies.
[QUOTE=”spareine, post: 5338523, member: 351563″]Why denying virtual objects?[/QUOTE]
I think you missed the point, as astronomer Berman said, “Rainbows are not 3D objects.” I too struggled with what that means.
Refer back to the diagram in the article that shows my eye, two drops (one high one low), and a sky image plus a lake image. Now suppose that the rain just began so that the high drop is there but there is no low drop. Then I will see the sky image but no lake image at all. Conversely, if the rain abruptly ended, the low drop could be there but no high drop, so I would see the lake image with no sky image. 3D objects, parallax, vanishing points, and virtual images are optical phenomena that propagate at the speed of light, so that if I saw the sky image I should simultaneously see the lake image.
The same applies if you stand beside me. Your eyes see rainbow light from different raindrops than my eyes see. Because those other raindrops may be missing, or have other properties, your eye sees a different rainbow than my eye. In most, [U]but not all[/U] circumstances, they look alike. That’s why the conventional optics rules for 3D images don’t apply.
The point may be clearer if we refer back to the article’s analogy with a man pointing a perfectly collimated laser at my eye. My eye sees the man and a red dot. My other eye (or you standing beside me) sees the man but no red dot. Conventional optics, including vanishing point, apply to the image of the man, but not to the red dot. The rainbow you see is more analogous to the red dot than to the image of the man.
[QUOTE=”OmCheeto, post: 5335695, member: 103343″]Being that the rainbow in the “What caused the Quadruple Rainbow?” thread looks suspiciously like your “mystery” rainbow, I’m going to guess that yours was a “reflected” rainbow.[/QUOTE]
I think you mean “reflection” rainbow, not “reflected” in the way that I used those terms in the article. The reflected rainbow is seen on the lake surface. The reflection rainbow is seen in the sky.
Very accessible Insight!
Yay! I love rainbows. :biggrin:
Way back in 2012, a forum member named Anna Blanksch started a thread, [URL=’https://www.physicsforums.com/threads/do-rainbows-have-differing-archs.639915/’][B][U]Do rainbows have differing archs?[/U][/B][/URL], which really started me thinking about them.
I’m pretty sure it was her fault that I started a thread, [B][U][URL=’https://www.physicsforums.com/threads/what-caused-the-quadruple-rainbow.809896/’]What caused the Quadruple Rainbow?[/URL][/U][/B], as they were just pretty things in the sky before that.
Being that the rainbow in the “What caused the Quadruple Rainbow?” thread looks suspiciously like your “mystery” rainbow, I’m going to guess that yours was a “reflected” rainbow.
This gets very high marks. I’ve already bookmarked it.
Excellent insight on observations people can make in their everyday life.
I wonder how a physicist can struggle so much with such an incredibly simple phenomenon as rainbows.
http://www.atoptics.co.uk/rainbows/seabow.htm
Running a true rainbow effect in POV-ray would be quite a challenge (POV-ray has an rainbow object, but is just a simulation). It has its limitations. While it can deal with refraction and reflection, in order to get effects like light bouncing off a reflective object illuminating another surface or for light passing through a refractive material to produce accurate caustics, you need to use a feature called "photons", which adds a great deal to the processing time. As a result, I had to limit myself to working with single objects, and even then I had to keep the dispersion samples (which determines how many colors the prismatic effect produces) down to a fairly low number which means the rainbow effects aren't all that smooth. Anyway, this is what I was able to come up with. the first is a cylinder seem end on, with the light coming from the right. The second is a "raindrop" or sphere. I don't know how illuminating they are towards the discussion, but they interesting to look at.One thing I should mention is that these are not perfectly accurate physical representations. One limitation is that once the white light is broken up in to its spectra, the refractive index for each color does not vary. In reality, each color would refract slightly differently. For instance, in the POV-ray model after passing light through a prism, passing it through a second prism will not reassemble the spectrum back into white light.
Interesting article! Maybe it is useful to add that your statement that two persons cannot see the same rainbow is a denial of the concept of virtual objects. If light rays can be traced back to an imaginary origin, that origin is called a virtual object. The rainbow is just a virtual object at infinity, no problem. Two persons watching the rainbow are looking at the same virtual object. Similarly, the reflection of a rainbow in the water is another virtual object. Why denying virtual objects?
Awesome Insight!
"Wikipedia says that the glory is believed to happen due to classical wave tunneling, when light nearby a droplet tunnels through air inside the droplet and is emitted backwards due to resonance effects."? Tunnels into an air bubble in inside the droplet?
Another source of a "twinned" rainbow is when you have both a regular rainbow, and a "reflection rainbow", at the same time. So if you see a twinned rainbow over a body of water, it seems the more likely explanation than that there are two sizes of drops.