Intro to the Millennium Prize Problems

Introduction

David Hilbert (1862-1943)

In this Insight, I will go over the background information for the Millennium Prize problems and briefly describe three of them. A future Insight will contain brief descriptions of the remaining four problems.

In 1900, David Hilbert presented 23 of the most important open problems in mathematics at a conference of the International Congress of Mathematicians at the Sorbonne in Paris. These became known as “Hilbert’s       Problems”. Effectively, Hilbert was laying out an agenda for 20th-century mathematics by picking and choosing the problems he judged to be the most important and difficult.  The problems spanned several disciplines, including number theory, calculus, set theory, and geometry. Over the next several decades, these problems generated an enormous amount of attention and effort in the mathematics community.

Some of the problems turned out to be easier than Hilbert guessed and were resolved quickly. A few others were stated too imprecisely to admit a solution. But the bulk of the problems were very hard, as anticipated. Any mathematician who successfully resolved one of the problems was vaulted into instant fame within the academic community, being revered on the same level as a Nobel laureate.

Over the next century, many other people presented problem lists, but none generated the same buzz and lasting impact as Hilbert’s problems. By the year 2000, most of Hilbert’s problems had been resolved, and the mathematics community was primed and ready for a new set of problems to be introduced. So on May 24, 2000, in Paris, the 100th anniversary of Hilbert’s problems was commemorated with the introduction of a new list of seven of the most important unsolved problems in mathematics. But there is more. The presentation, delivered by Sir Michael Atiyah (GB) and John Tate (USA), was capped with the announcement that these seven problems would carry a bounty of $1,000,000 each, and would be known as the Millennium Problems.

Landon T. Clay (1926 – )

The prize money- 7 million dollars in total- was furnished by a wealthy American businessman and math enthusiast named Landon Clay. Clay established the Clay Mathematics Institute (CMI) in 1998 in his hometown of Cambridge, Massachusetts as a nonprofit organization to organize the Paris Meeting and administer the Millennium Problems Competition. From their website,

“The prizes were established by CMI to (i) recognize some of the arguably most difficult problems with which mathematicians were struggling at the turn of the millennium, (ii) to underline the importance of working on the really hard problems, and (iii) to spread the news that in mathematics hard, significant problems still abound – the frontiers of knowledge are still wide open.”

Since there is prize money involved, there is a bit more process to solving one of the Millennium problems than one of Hilbert’s problems. Solutions are not submitted directly but instead must be published in a mathematics journal of worldwide repute. The solution must then withstand scrutiny by members of the mathematics community for the next two years. After this two-year waiting period, the CMI organizes a panel that includes experts in the area of the problem, and the panel decides whether to recommend awarding a prize for the solution (full rules here).

Up until now, in 2015, only one of the Millennium problems has been successfully solved, and the $1,000,000 prize was famously turned down by the man who solved it.

So, what are the Millennium problems? As you’ll see in just a moment, they are quite hard and worthy of your attention. And if you put in enough hard work, you just might be able to claim one of the remaining $1,000,000 prizes for your efforts.

Each section below briefly describes a problem and contains a link to the official problem description. Since I am not claiming to be an expert in the subject areas of these problems, I would advise you to refer to the official problem descriptions for details. Note that the official problem descriptions also define alternative ways to prove or disprove the theorems!

1.  Poincaré Conjecture (Topology)

Status:    Solved by Grigoriy Perelman

Official Problem Statement:    http://www.claymath.org/sites/default/files/poincare.pdf

Description:

Henri Poincaré (1854 – 1912)

The only Millennium problem to be solved thus far, the Poincaré conjecture has to do with the topological properties of three-dimensional manifolds.

Lines and circles are examples of one-dimensional manifolds. Two-dimensional manifolds, or surfaces,  include the plane, the sphere, and the torus.

You may have heard that in Topology, a donut is the same as a coffee cup. Both objects have 1 hole, so they can be continuously deformed into one another. All surfaces have a well-defined genus or number of holes, that can be used to characterize them in this manner.

The Poincare conjecture extends this idea to higher dimensional manifolds, the simplest of which is the unit sphere $x^2+y^2+z^2+w^2=1$. Poincare noticed that if you draw any simple closed curve on a two-dimensional unit sphere, then it can be continuously deformed down to a single point without leaving the sphere. He then wondered if this condition could be used to prove that two higher-dimensional manifolds are homeomorphic:

If a compact three-dimensional manifold M3 has the property that every simple closed curve within the manifold can be deformed continuously to a point, does it follow that M3 is homeomorphic to the sphere S3?

The hypothesis that every simply connected closed 3-manifold is homeomorphic to the 3-sphere is known as the Poincaré Conjecture.

 

2.  P versus NP (Computer Science)

Status:    Unsolved

Official Problem Statement:    http://www.claymath.org/sites/default/files/pvsnp.pdf

Description:

The P vs. NP problem, first mentioned in a 1956 letter penned by Kurt Gödel, has become ubiquitous in modern computer science. The problem is stated simply:

Can every problem that can be easily checked by a computer (NP) also be easily solved by a computer (P)?

Since we are talking about computer solutions, “easily” normally means “in polynomial time”. If a problem can be solved in polynomial time, then the time needed to solve it increases relatively slowly as the problem size increases. In contrast, some problems become impossibly slow and difficult to solve as soon as the problem size is increased (for example, an exponential increase in difficulty).

It is trivial that P problems are also NP problems because the P problem can be solved easily and the result can be used to easily check a proposed solution. However, NP problems are not necessarily always easy to solve. It remains unclear whether all NP problems are also P problems, or if some NP problems lie outside this boundary.

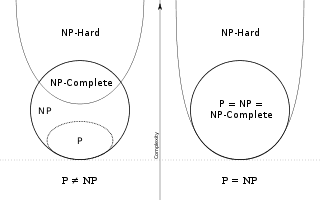
Wikipedia diagram outlining the relation between P, NP, NP-Complete, and NP-Hard problems in each case.

A classic example is the partitioning problem. Let’s say you have 100 rocks and want to put them into two piles of equal mass. If you guess the solution then it is easy for a computer to check if the guess is correct, so this is an NP problem. However, there are $2^{100}$ possible ways for the computer to divide 100 rocks into 2 piles, making the problem difficult to solve with a brute force approach.

The core of this issue is that if all NP problems are P problems ($P = NP$), then there are very fast ways to solve NP problems that we just don’t know about yet. In the case of the partitioning example, this would mean that there is a fast way for a computer to divide the rocks into two equal-mass piles without checking all $2^{100}$ combinations.

As it turns out, there are further classifications that help sort out whether $P = NP$, because not all NP problems are created equally. A problem is called NP-Hard if it is at least as hard as the hardest NP problems. In other words, a problem is NP-Hard if there exists a way to reduce every other NP problem into it. The ramification of this is that if you solve an NP-Hard problem, you have essentially also provided a quick way to solve all NP problems. A common example of an NP-Hard problem is the traveling salesman problem: if you have a list of cities and the distances between each, what is the fastest route to stop at each city once and go back to the starting point? The complexity of this problem increases substantially with the number of cities.

Furthermore, a problem is NP-Complete (or NPC) if it is both NP (easily verified) and NP-Hard (every NP problem can be reduced into it). Many NP-Complete and NP-Hard problems are so hard that they can only be approached with approximation techniques.

If $P\ne NP$, then NP-Hard problems cannot be solved quickly (as on the left side of the diagram above). However, if P=NP, then since all NP-Complete problems are NP, you get P=NP=NPC, and the subset of NP-Hard problems that are NP-Complete can be solved quickly (as in the right side of the diagram above).

The ramifications of a solution to whether $P = NP$ would be enormous. For example, optimization problems (such as the traveling salesman) that currently can only be approximated could be solved exactly, public-key cryptography would be greatly weakened as the math problems it relies on would become “easy”, and artificial intelligence would take a giant leap forward as learning tasks become greatly simplified (think about the implications of perfect speech recognition or language translation).

 

3.  Riemann Hypothesis (Number Theory)

Status:    Unsolved

Official Problem Statement:    http://www.claymath.org/sites/default/files/official_problem_description.pdf

Description:

Bernhard Riemann (1826 – 1866)

The origin of this problem dates back to November 1859 when Bernhard Riemann published a paper entitled “On the Number of Prime Numbers less than a Given Quantity“. As the title suggests, Riemann derived a formula that gives the number of prime numbers less than a given number. During this investigation, Riemann studied a function called the zeta function extensively. The zeta function, defined for complex $s$ in the half plane defined by $\mathbb{R}(s)>1$, is:

$$\zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s} = \frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}…$$

The connection between prime numbers and the zeta function is what led Riemann down this path. The formula that he eventually derives for the number of primes is defined in terms of the zeros of the zeta function. Much earlier, in 1748, Euler made an incredible connection by showing that the zeta function can be expressed as an infinite product over all prime numbers $p$:

$$\zeta(s) = \prod_{p} \frac{1}{1-p^{-s}} = \frac{1}{1-2^{-s}} \cdot \frac{1}{1-3^{-s}} \cdot \frac{1}{1-5^{-s}} \cdot …$$

This formula is known as the Euler product. The series converges for complex $s$ with real parts larger than 1. This connection provides the starting point for Riemann’s investigation.

During the investigation, Riemann wanted to analyze the zeta function of overall complex numbers. However, to analyze these values it is necessary to redefine the function so that it is valid over the whole complex plane (recall that the formula above is only defined for complex $s$ with real part larger than 1). The process of redefining the function to be valid over a larger area of numbers is called analytic continuation. The new expression, valid for $0<\mathbb{R}(s)<1$, is

$$\zeta(s) = 2^s \pi^{s-1} \sin \left( \frac{\pi s}{2} \right) \Gamma (1-s) \zeta(1-s)$$

A quick explanation of the zeros of this expression from Wikipedia:

If s is a negative even integer then ζ(s) = 0 because the factor sin(πs/2) vanishes; these are the trivial zeros of the zeta function… The value ζ(0) = −1/2 is not determined by the functional equation, but is the limiting value of ζ(s) as s approaches zero. The functional equation also implies that the zeta function has no zeros with negative real part other than the trivial zeros, so all non-trivial zeros lie in the critical strip where s has real part between 0 and 1.

Later in the paper, Riemann introduces a complex function defined in terms of $s=1/2 + it$:

$$\xi(t) = \frac{1}{2} s(s-1) \pi^{-s/2} \Gamma \left( \frac{s}{2}\right) \zeta(s)$$

He proves several properties of this function and begins to sketch a proof about where the zeros are. Then, on the fifth page of his paper, Riemann states:

…One now finds indeed approximately this number of real roots within these limits, and it is very probable that all roots are real. Certainly one would wish for a stricter proof here; I have meanwhile temporarily put aside the search for this after some fleeting futile attempts, as it appears unnecessary for the next objective of my investigation.

Put simply, the Riemann hypothesis is the positive proof of this statement: that all of the roots of $\xi(t)$ are real. However, this function is defined in terms of the zeta function, which has nontrivial zeros at the values $1/2 + i \alpha$, where $\alpha$ is a zero of $\xi(t)$. This leads to the much more common statement of the problem: the Riemann hypothesis is that all of the nontrivial zeros of $\zeta(s)$ lie on a vertical straight line with a real part equal to $1/2$.

Up until now in 2015, computers have verified that billions of zeros lie on this so-called critical strip. But to be certain, the world needs complete proof.

One of only a few of Hilbert’s problems to survive unsolved for over a century, the Riemann hypothesis has proved to be very resilient to many different angles of attack. Still, with computers hacking away and verifying billions of zeros to the function, many believe that the Riemann Hypothesis is true and that the proof simply remains elusive.

Countless papers assume the validity of the Riemann hypothesis, and positive proof here would provide a more substantial footing for these results. However, it is also likely that proof of the Riemann hypothesis will reveal the deep structure of the prime numbers, which has vast implications (not the least of which relates to cryptography and the security of the entire internet!)