An Alternative Approach to Solving Collision Problems

Introduction

Collisions are very much a stock item in any school physics curriculum and students are generally taught about the use of the principles of conservation of momentum and energy for solving simple collision problems in one dimension. In this article we will be examining a very common type of collision problem: the inelastic collision. (See Note 1 below: a review comment on the definition of an inelastic collision)  However we will be following a somewhat unconventional approach which – notwithstanding – is very much in step with a key underlying physical law namely Newton’s third law upon which conservation of momentum rests. We develop some easy to use formulae for the solution of inelastic collisions and show that these may be easily modified to solve both perfectly elastic and ‘semi-elastic’ collision problems.

Conservation of Momentum re-arranged

The basic equation for conservation of momentum in a straightforward collision between two masses $m_1$ and $m_2$ with velocities $v_1$ and $v_2$ is as follows: (to keep things simple – ie one dimensional – we are not using vector notation for the velocities although it should be assumed values can be either positive or negative depending on the collision dynamics and the choice of positive direction). $$m_1v_{1i}+m_2v_{2i}=m_1v_{1f}+m_2v_{2f}$$

Re-arranging: $$-(m_1v_{1f}-m_1v_{1i})=m_2v_{2f}-m_2v_{2i}$$Finally dividing through by the collision interval $Δt$, we can write: $$\frac{-Δp_1}{Δt}=\frac{Δp_2}{Δt}$$For every action there is an equal and opposite reaction!

Collision Impulse

Since the collision interval $Δt$ is common and can therefore be cleared on both sides of the equation, we can phrase Newton 3 as something like “in a collision between two masses, the collision impulses experienced by the respective masses are equal and opposite“.  Further in the particular case of a perfectly inelastic collision, we can seek to determine an algebraic expression for this ‘equal and opposite’ collision impulse. And thereby enable a very straightforward calculation for determination of the final velocity of the two masses: $$v_f=\frac{p_1+Δp_1}{m_1}=\frac{p_2+Δp_2}{m_2}$$Some fairly ‘inelegant’ algebra is now required (see Note 2 below for an easier way) to reach a  simple but (dare I say) elegant formula for collision impulse. We begin with conservation of momentum for an inelastic collision in which the final velocities of the colliding masses are the same:

$$m_1v_{1i}+m_2v_{2i}=m_1v_{f}+m_2v_{f}$$ $$⇒v_f=\frac{m_1v_{1i}+m_2v_{2i}}{m_1+m_2}$$ $$Δp=m_1v_f-m_1v_{1i}=m_1\frac{m_1v_{1i}+m_2v_{2i}}{m_1+m_2}-m_1v_{1i}\frac{m_1+m_2}{m_1+m_2}$$ $$=\frac{m_1m_2}{m_1+m_2}(v_{2i}-v_{1i})=μΔv$$

Collision impulse is simply the product of the ‘reduced mass’ of the colliding bodies and their relative velocity (before collision). Reduced mass given by the equation $\frac{m_1m_2}{m_1+m_2}$ and relative velocity turn out to be key collision parameters as will further be evidenced when we seek to obtain an expression for energy loss during an inelastic or “collide and coalesce” collision.

Energy Loss during Collision

To calculate the energy loss during a perfectly inelastic collision we use the equation: $$ΔE=KE_i-KE_f$$ We expect a further round of somewhat hair raising algebra! $$=\frac{{p_1}^2}{2m_1}+\frac{{p_2}^2}{2m_2}-\frac{{(p_1+Δp)}^2}{2m_1}-\frac{{(p_2-Δp)}^2}{2m_2}$$

Note that we have dispensed with the notation $Δp_1$ and $Δp_2$ in favour of simply $Δp$ and $-Δp$ in keeping with Newton 3. $$= \frac{{-(Δp)}^2}{2}\left(\frac{1}{m_1}+\frac{1}{m_2}\right)+Δp\left(\frac{p_2}{m_2}-\frac{p_1}{m_1}\right)$$ At this juncture we substitute for $Δp$: $$=\frac{-{(μΔv)}^2}{2μ}+μΔv(Δv)=½μ{(Δv)}^2$$ The loss in kinetic energy is equivalent to the energy of a mass equal to the reduced mass of the colliding bodies having a velocity equal to their relative velocity.

Extension to Elastic and Semi-elastic Collisions

In order to expand these concepts to other types of collisions , one approach would be to slog through further algebra. However a much simpler method arises from the recognition that the physics of the above perfectly inelastic collision is mathematically equivalent to a collision between a single body having a mass corresponding to the reduced mass  (and velocity equal to the relative velocity Δv)  and a wall of infinite mass.  Once this realisation has dawned, it only takes a few moments to write down similar equations for the collision impulses in perfectly elastic and semi-elastic collisions:

Perfectly elastic: $Δp=2μΔv$

Semi elastic: $Δp=μ(1+e)Δv$ where e is the co-efficient of restitution.

Energy loss in semi-elastic collision: $ΔE=½μ{(Δv)}^2(1-e^2)$. Note that this simplifies to zero in the case of a perfectly elastic collision and $½μ{(Δv)}^2$ in the case of a perfectly inelastic collision.

Summary of Formulae and Conclusion

Transfer of Momentum

Perfectly inelastic collision: Δp=μΔv

Semi-elastic collision: Δp=μ(1+e)Δv

Perfectly elastic collision: Δp=2μΔv

Energy Loss

Perfectly inelastic collision: ΔE=½μΔv²

Semi-elastic collision: ΔE=½μΔv²(1-e²)

Perfectly elastic collision: ΔE=0

The reader is encouraged to try out the above formulae to solve collision problems- they should be as widely applicable as are the principles of conservation of energy and momentum since that is their genesis!

Appendix: Worked Examples

Armed with the above set of formulae, we are ready to tackle just about any non relativistic collision problem which might arise (possibly the formulas could even be adapted for relativistic collisions).  We expect our solutions to be  simpler than those obtained using the principles of conservation of momentum and energy because through the algebraic process presented above, we have already ‘pre-solved’ the equations that arise through the application of these principles. 

1. Head-on Collision Problem

The following collision problem is an extract from a National Senior Certificate (South Africa) Physics Paper: November 2011.

Solution

Take East as the positive direction.

Our solution strategy will be to calculate the collision impulse Δp and add/subtract it from the momentum values of the respective vehicles to determine the final momentum of each. Division by the respective masses should then yield the same result for velocity since this is a collide and coalesce collision.

Relative Velocity (of car relative to truck): 40 – (-20) = 60 m/s. Reduced Mass = 1000 x 5000 / (1000 + 5000)

Collision Impulse (car on truck): Δp = μΔv = 1000 x 5000 / 6000 x 60 = 50000 Ns.

Collision Impulse (truck on car): = -50000 Ns (Action and Reaction are equal and opposite!)

Final Momentum of Car: p_car – Δp = 40 x 1000 – 50000 = -10000 Ns

Final velocity of car is -10000/1000 = – 10 m/s.

Final Momentum of Truck: p_truck + Δp = -20 x 5000 + 50000 = -50000 Ns

Final velocity of truck is -50000/5000 = -10m/s (note that we didn’t really need this but it does verify the calculation for the car’s final velocity)

Force of truck on car: -50000 / 0.5 = -100 000 N. This force could cause fatal injury.

Collision Energy loss (if required): ½μΔv² = 0.5 x 1000 x 5000 / 6000 x 3600 = 1.5 M Joules.

2. More Difficult Problem

This  ‘Tarzan’ type problem involving another perfectly inelastic collision is drawn from one of the homework forums on PF.

Jane thinks that Tarzan has been gaining too much mass. However, he doesn’t want to tell her what he weighs. One day Tarzan is swinging in the forest. He starts from rest from one side at an angle of 53° from the vertical. He swings down and grabs Jane at the bottom of the swing. They swing together on the other side up to a maximum angle of 37 °. Jane knows that her mass is 50 kg. Calculate Tarzan’s mass. (Ans.120.8kg)

Solution

Method 1: Transfer of Momentum

Here we employ the formula $Δp=μΔv$ to obtain Jane’s post-collision momentum which will be just Δp since she is initially at rest. Then divide by her mass to obtain the post-collision final velocity.  In this case the initial Δv is obtained by converting Tarzan’s PE to KE ie $Δv=\sqrt{2gh_1}$. Let Tarzan’s mass be m – then: $$v_f=\frac{Δp}{50}=\frac{m}{m+50}\sqrt{2gh_1} $$Converting KE back to PE for the final height attained, we have ${v_f}^2=2gh_2$ Thus: $${\left(\frac{m}{m+50}\right)}^2*2gh_1=2gh_2$$ $${\left(\frac{m}{m+50}\right)}^2=\frac{h_2}{h_1}=\frac{1-cos(37)}{1-cos(53)}$$Letting Wolfram Alpha process this equation, we obtain m=123.09 kg.

Method 2: Use energy loss formula

Begin by setting ground level to be where Jane is so that Tarzan’s initial height above her is l(1-cos53) and the final height they both attain following inelastic collision with Jane is l(1-cos37) where l is the length of Tarzan’s vine. Tarzan’s velocity just before ‘collecting’ Jane will be $\sqrt{2gl(1-cos53)}$ from equating gain in KE to loss in PE. All we need do is equate the loss in PE to the collision energy loss $½μ{(Δv)}^2$. Let Tarzan’s mass be m: $$mgl(1-cos(53))-(m+50)gl(1-cos(37))=0.5*\frac{50m}{m+50}*2gl(1-cos53) $$ Plainly gl cancels out and we can ‘feed’ the remaining equation straight to Wolfram Alpha obtaining a value of 123.088 kg for Tarzan’s mass. This is a little different from the given solution but essentially the same as obtained by Method 1 above. (See Note 3 for a convincing explanation of the discrepancy)

3. Elastic Collision

This is a solution to Problem 3 of Problem Set 9 from MIT. The setup is a cube  of mass $m_c$ sliding on a frictionless table with velocity $v_c$ colliding with an initially stationary curved block mass $m_b$ also on the frictionless table – hence free to move. We are required to find expressions for:

a) the maximum height which the cube reaches when sliding up the (also frictionless) curved face of the block.

b) the final speeds of block and cube after the latter has slid back down the curved face and separated from the block.

Solution

Part a) can be quickly solved by noting that when the cube reaches maximum height on the curved block, the two are momentarily at rest with respect to each other. This is essentially a condition which is otherwise met during the course of an inelastic collision. The difference here is that the inelastic collision energy ½μ(Δv)² is not lost – it is simply converted to PE. We may therefore equate: $½μ(Δv)²=m_cgh$ from which we obtain: $$ h=\frac{m_b{v_c}^2}{2g(m_c+m_b)}$$

For Part b) once the cube has slid back down the face of the block and recovered its kinetic energy, the situation is simply a post-collision elastic impact in which – per formula above – the collision impulse is 2μΔv. Since the block was initially at rest , its final momentum will be 0 + 2μΔv and all we need do is divide by $m_b$ to obtain the final speed of the block: $$v_{bf}=\frac{2m_cv_c}{m_b+m_c}$$. For the final momentum of the cube, simply subtract 2μΔv from the initial momentum $m_cv_c$ and divide by $m_c$ for the cube’s final speed: $$v_{cf}=v_c\left(1-\frac{2m_b}{m_c+m_b}\right)=v_c\left(\frac{m_c-m_b}{m_c+m_b}\right) $$

4. Collision of Atomic Particles

This example is a solution to Problem 5 of  another MIT problem set (Problem Set 7: Fall 2012).

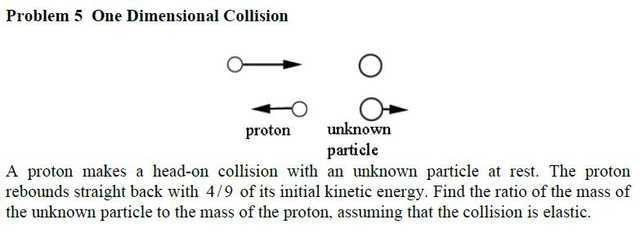
Let the mass of the proton be m and the mass of the unknown particle km with k>1. Since the unknown particle is initially at rest, its post collision momentum will be the same as the collision impulse and so we can easily calculate an expression for its kinetic energy and compare with 5/9 the kinetic energy of the proton.

For an elastic collision: $$\Delta P=2\mu\Delta v = 2 \frac{km^2}{m(k+1)} \Delta v = 2\frac{k}{k+1}m\Delta v$$ Post collision kinetic energy of the unknown particle will be ${\Delta P}^2/(2km)$ $$\frac{4k^2m^2{\Delta v}^2}{2km(k+1)^2}=5/9 \times ½m{\Delta v}^2 $$ $$\frac{2k}{(k+1)^2}=\frac{5}{18}$$ $$36k=5k^2+10k+5$$ $$⇒(5k-1)(k-5)=0$$Hence since k>1 we determine k=5.

Acknowledgements and Notes

I would like to thank PF staff members Charles Link and Haruspex for kindly reviewing this article. The “Head-on” collision example above as well as the following notes (referenced in the text) are included arising from these reviews.

Note 1

You do not actually define perfect inelasticity. You implicitly take it as coalescence, which is ok for the one dimensional (head on collision) case. More generally I define it as maximum loss of KE consistent with momentum conservation.

Note 2

A simpler technique for deriving the collision impulse is suggested by PF user Haruspex:

Start with a1=F/m1, so a2=-F/m2 and relative acceleration a1-a2=F(1/m1+1/m2).  Integrating yields $\Delta v_{rel}=\Delta p/\mu$.

Note 3

Whenever I see angles like 37 degrees I think, ah yes, 3-4-5 triangle. Taking the trig function values to be 0.6 and 0.8 gives a mass $\frac{50}{\sqrt 2-1}=120.7$.

References

[1]	Isaac Newton. Philosophiae Naturalis Principia Mathematica. William Dawson & Sons Ltd., London, 1687. [ bib ]
[2]	National Department of Basic Education > Curriculum > National Senior Certificate (NSC) examinations > NSC 2011 November exam papers.https://www.education.gov.za/Curriculum/NationalSeniorCertificate(NSC)Examinations/NSC2011NovemberExampapers.aspx. (Accessed on 02/03/2020). [ bib ]

Comment Thread