The Unreasonable Effectiveness of the Popescu-Rohrlich Correlations

In this Insight, I will show how the Popescu-Rohrlich (superquantum) correlations provide an unreasonable advantage in a particular “quantum guessing game” using a pedagogical counterpart from the book “Totally Random: Why Nobody Understands Quantum Mechanics” by Tanya Bub and Jeffrey Bub (Princeton University Press, 2018).

As I showed in my Insight Why the Quantum, the PR correlations violate conservation of spin angular momentum (or “conservation per no preferred reference frame” more generally [1], as I will explain below), so it doesn’t seem likely they can be physically instantiated. But if the PR correlations could be instantiated, they (the Bubs or “Bub” for short) point out the PR correlations would afford an amazing advantage in a “quantum guessing game” that Bub labels the “Distributed Computing Challenge” in their “Quantum Quasino” (figure below).

The Popescu-Rohrlich (PR) correlations are represented by special coins that obey (super)quantum rules of entanglement called “Quoin Mechanics” when flipped (so the coins are called “quoins,” figure below).

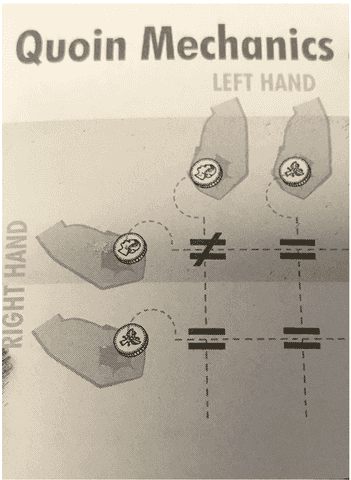
If both coins start as heads, they will end up tails-heads or heads-tails, never heads-heads or tails-tails (“not equal” in the figure above). Given any other starting configuration, i.e., tails-tails or tails-heads or heads-tails, they will end up “equal,” i.e., heads-heads or tails-tails. These are magical coins indeed and as Bub shows their behavior cannot be explained by any “rigging” based on their starting positions.

To show this, they note there are only four ways to “rig” a quoin:

1. No matter how it starts, it ends up heads (h).
2. No matter how it starts, it ends up tails (t).
3. It stays the same way it starts (s for same).
4. It changes from the way it starts (o for other).

They then list all the possible riggings for a heads-heads (HH) start that yield non-equal outcomes (figure below). They also list all the possible riggings for a heads-tails (HT) or tails-heads (TH) or a tails-tails (TT) start that yield equal outcomes (figure below). We then must search the table to find a rigging that can yield the Quoin Mechanics, i.e., a rigging that exists in every column. But, from the figure below we see that there are none. Therefore, we simply have to accept Quoin Mechanics without knowing how they are instantiated in order to explore their implications for our quantum guessing game.

Note, we found something similar in trying to explain quantum correlations that violate Bell’s inequality using Mermin’s “instruction sets” in Why the Quantum and Answering Mermin’s Challenge with Wilczek’s Challenge. In that case for quantum correlations, as with these superquantum correlations, the instruction sets didn’t work and we were left with no `causal mechanism’ to explain the quantum correlations. The difference is of course that while we don’t have any `causal mechanism’ to explain quantum correlations we can and do instantiate them in the lab. And, as I showed in Why the Quantum, quantum correlations do obey a very reasonable conservation principle (conservation per no preferred reference frame) while PR correlations violate that principle. I will briefly discuss the quantum information counterpart to this conservation principle later, but first I will show how these conservation-violating PR correlations are `miraculous’ in their information exchanging capability. Let’s start with the game itself.

As you can see in the first figure, there are 5 lanes on each side of the partition (a sign reading “Distributed Computing Challenge”). The lanes are numbered 1 through 5 and the game is started by the dealer (man shown who bears a striking resemblance to Jeff Bub!) setting values of 1 or 0 for each of the ten lanes (figure below). After the dealer has set these ten values, we see that there are some lanes on both sides that both have a 1 (lanes 1 and 4 in the figure below). The person on the right is the “guesser” and she (in this game it’s a female, in others it’s a male) doesn’t know what the person on the left has in his (in this game it’s a male, in others it’s a female) lanes. Her job is to guess whether there are an even number of lanes that have a 1 on both sides (as is the case in the figure below) or an odd number of such lanes. The only way she can know the answer is if the dealer were to set all five of her lanes to 0 in which case she knows the answer is even, i.e., there are zero lanes that have a 1 on both sides. Of course, the dealer isn’t going to do that, so she will always have at least one 1 on her side. For all such cases, it is not difficult to convince yourself that the probability of the right answer being odd(even) is 50%(50%). You buy six bit coins to play and the House doubles your coins for a correct guess. If you guess wrong, you lose all your coins to the House. Since the odds are 50-50 of guessing right, you’ll end up breaking even if you continue to play, meaning you’ll not win or lose money overall.

 

But, there is another aspect of the game that I have not told you — the person on the left can spend one bit coin to send one piece of information to his guessing partner on the right. In that case, the partners have five bit coins remaining and if they win, the House pays them five bit coins, i.e., the House doubles their remaining coins. Likewise, the person on the left can spend two bit coins to send two pieces of information to the guessing partner on the right which means the House would pay four bit coins if they win. Once they have to spend three bit coins to win, the House pays three bit coins and they break even monetarily by winning the game. Bub represents this by showing the guessing contestant (a fox in the figure below) having his partner send him the values in her lanes 1, 2 and 3, so he can see if she has any 1’s in those lanes. That’s all the information he needs, since he has 0’s in lanes 4 and 5. She sends the bits 0, 0, and 1 which tell him they have just one lane (lane 3) where they both have a 1, so the answer is “odd.” They win the game and three bit coins, but they spent three bit coins to send the three bits of information, so they broke even monetarily. You can easily convince yourself that this strategy would actually end up losing money in the long run.

Now it’s time to show how a pair of contestants with quoins can win this game every time by merely passing one bit of information each game, thereby winning five bit coins every game, i.e., netting four bit coins every game. Here is Bub’s strategy. The contestants start with five pairs of quoins. [Don’t confuse these with the six bit coins they bought from the House to play the game, they brought these five pairs of quoins with them to the Quasino.] Bob is the guesser and Alice will be sending him one bit of information. Alice’s quoins are labeled 1A, 2A, 3A, 4A, 5A and Bob’s are labeled 1B, 2B, 3B, 4B, 5B. Quoins 1A and 1B are entangled per Quoin Mechanics, as are 2A and 2B, etc. The strategy is simple although the reasoning behind it is not trivial. Let’s start with the reasoning behind the strategy.

Whenever either or both of Alice and Bob start with tails, they both get the same result (Quoin Mechanics). So, in all trials (pairs of flips) where either or both starts with tails they both have an odd number of heads (“odd-landing camp”) or an even number of heads (“even-landing camp”), since they get the same results in every trial (Quoin Mechanics). Suppose there is one trial where they both start with heads. That means they get opposite results (Quoin Mechanics), so now Alice and Bob are in opposite landing camps. Now suppose there are two trials where they both start with heads. Since they again get opposite results, Alice and Bob are once again in the same landing camp. You can see where this is going, right? If Alice and Bob have an odd number of trials where they both start with heads, they will be in opposite landing camps. If Alice and Bob have an even number of trials where they both start with heads, they will be in the same landing camp. Since they’re looking for even or odd pairings of 1’s in their lanes, all they have to do is flip each entangled quoin starting with heads in all lanes where they have a 1 and flip each entangled quoin starting with tails in all lanes where they have a 0, making sure to align lane number with quoin number.

For example,  Alice flips her quoin 1A starting on heads if her lane 1 has a 1 and she starts it on tails if her lane 1 has a 0. She does this for each of the other quoins and lanes. Bob does the same with his quoins. If they are in opposite landing camps after doing this, they know there are an odd number of trials where they both started with heads, so Bob knows there are an odd number of lanes with 1’s on both sides. If they are in the same landing camp after doing this, they know there are an even number of trials where they both started with heads, so Bob knows there are an even number of lanes with 1’s on both sides. Thus, all Bob needs to know after flipping his five quoins is what landing camp Alice is in and she can send him that one piece of information (1 for odd and 0 for even, for example) by spending just one bit coin. Thus, Quoin Mechanics guarantees they will win five bit coins every game (netting four).

How egregious is this advantage? In other words, can quantum correlations achieve anywhere near this success rate? Let’s look at the PR correlations
\begin{equation}\begin{split}&P(1,1 \mid a,b) = P(-1,-1 \mid a, b)=\frac{1}{2}\\
&P(1,1 \mid a,b^\prime) = P(-1,-1 \mid a, b^\prime)=\frac{1}{2}\\
&P(1,1 \mid a^\prime,b) = P(-1,-1 \mid a^\prime, b)=\frac{1}{2}\\
&P(1,-1 \mid a^\prime,b^\prime) = P(-1,1 \mid a^\prime, b^\prime)=\frac{1}{2} \end{split}\label{PRcorr}\end{equation}
We see that the the fourth PR correlation corresponds to the HH case producing unequal outcomes in Quoin Mechanics. That is, using $a = b$ = T and $a^\prime = b^\prime$ = H with outcomes +1 = H and –1 = T, the PR correlations align with Quoin Mechanics. Since it is the HH case that allows us to discern even or odd pairs of 1’s in our guessing game using only one bit of information, let’s scrutinize the fourth PR correlation using our conservation principle.

To do this, let’s consider the general conservation principle at work in the four Bell basis states
\begin{equation}
\begin{split}
&\frac{1}{\sqrt{2}} \left(\mid +1-1 \rangle – \mid -1+1 \rangle \right)\\
&\frac{1}{\sqrt{2}} \left(\mid +1-1 \rangle + \mid -1+1 \rangle \right)\\
&\frac{1}{\sqrt{2}} \left(\mid +1+1 \rangle + \mid -1-1 \rangle \right)\\
&\frac{1}{\sqrt{2}} \left(\mid +1+1 \rangle – \mid -1-1 \rangle \right)\\ \label{bellstates}
\end{split}
\end{equation}
The eigenvalues for any $2\times 2$ Hermitian matrix can be written +1 and –1, so whatever Alice and Bob are measuring as represented by the Bell basis states it gives outcomes of +1 or –1. As I showed in Bell States and Conservation of Spin Angular Momentum, the states are invariant in Hilbert space under an appropriate transformation, which leads to conservation of whatever the states represent. So, whatever the various measurement settings represent, Bob and Alice always measure unlike results in like settings for the first state (“unlike state” aka the “singlet state”) and like results for like settings for the last three states in the plane of symmetry (“like states” aka the “triplet states”) evidencing conservation of binary information, e.g., on-on(ness) or on-off(ness) or yes-no(ness). According to quantum mechanics, which satisfies conservation of whatever the binary results represent (see [1], Why the Quantum, and Answering Mermin’s Challenge with Wilczek’s Challenge), the probability of measuring unlike results for the singlet state is $\mbox{cos}^2\theta$ and the probability of measuring like results for the singlet state is $\mbox{sin}^2\theta$ where $\theta$ is the angle between the basis vectors in Hilbert space. If you don’t know what that means, don’t worry, you can still follow the argument. Similarly, per our conservation-obeying quantum mechanics, the probability of measuring like results for the triplet states is $\mbox{cos}^2\theta$ and the probability of measuring unlike results for the triplet states is $\mbox{sin}^2\theta$ (in the appropriate Hilbert space plane as shown in Bell States and Conservation of Spin Angular Momentum).

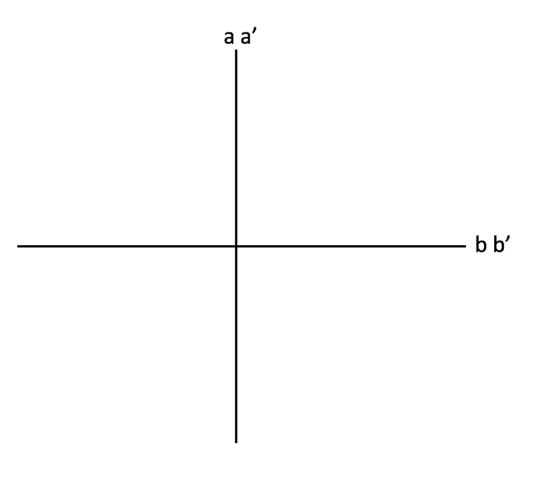
Start with the singlet state. The first PR correlation says that the basis vectors for measurements $a$ and $b$ must be perpendicular (figure below). That is, the first PR correlation has only like results for measurements $a$ and $b$ on the singlet state, so $\mbox{sin}^2\theta$ must be equal to 1 to satisfy quantum probability and thus, our conservation principle. The second PR correlation says $a$ and $b^\prime$ must be perpendicular (like results for the singlet state, $\mbox{sin}^2\theta = 1$, figure below). And, the third PR correlation says $a^\prime$ and $b$ must be perpendicular (like results for the singlet state, $\mbox{sin}^2\theta = 1$, figure below). Thus, these three PR correlations in total say $a^\prime/a$ is perpendicular to $b^\prime/b$ (figure below). So, we need the fourth PR correlation to say $a^\prime$ and $b^\prime$ are perpendicular, but of course it says that $a^\prime$ and $b^\prime$ must be parallel (unlike results for the singlet state, $\mbox{cos}^2\theta = 1$). Therefore, the PR correlations violate our constraint (conservation of binary information) in a maximal fashion for the singlet state.

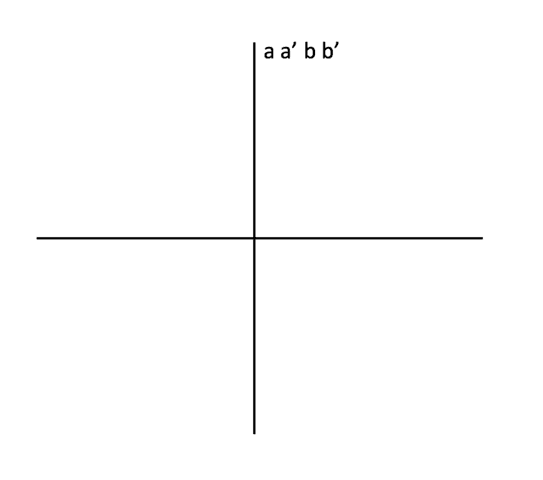
Now for the triplet states. The first PR correlation says that $a$ and $b$ must be parallel (like results for the triplet states, $\mbox{cos}^2\theta = 1$, figure below). The second PR correlation says $a$ and $b^\prime$ must be parallel (like results for the triplet states, $\mbox{cos}^2\theta = 1$, figure below).  And, the third PR correlation says $a^\prime$ and $b$ must be parallel (like results for the triplet states, $\mbox{cos}^2\theta = 1$, figure below). Thus, these three PR correlations in total say $a$, $a^\prime$, $b$, and $b^\prime$ are all parallel (figure below). So, we need the fourth PR correlation to say $a^\prime$ and $b^\prime$ are parallel, but of course it says $a^\prime$ and $b^\prime$ must be perpendicular (unlike results for the triplet states, $\mbox{sin}^2\theta = 1$). Therefore, the PR correlations also violate our constraint (conservation of binary information) in a maximal fashion for the triplet states.

Therefore, in order to satisfy our conservation of binary information (per quantum correlations) we need the outcomes of a HH start to be equal just as the outcomes of a TH, HT, or TT start. But, if we make the outcomes of a HH start equal, we lose the advantage of Quoin Mechanics. In fact, using quantum coins (the outcomes of a HH start are equal) instead of superquantum quoins (the outcomes of a HH start are not equal) puts us right back to a 50-50 chance of winning the guessing game (recall the reasoning behind the quoin strategy). So, we see that the PR correlations are not just a little bit better than quantum correlations for the quantum guessing game, they are unreasonably effective. But, again, they violate our conservation of binary information, which translates into conservation of spin angular momentum on average when the information regards spin as I showed in Why the Quantum and Answering Mermin’s Challenge with Wilczek’s Challenge. So, it is probably the case that a physical instantiation of the PR correlations is a pipe dream akin to a perpetual motion machine.

 

References

1. W.M. Stuckey, M. Silberstein, T. McDevitt, and I. Kohler, “Why the Tsirelson Bound? Bub’s Question and Fuchs’ Desideratum,” Entropy 21, 692 (2019).