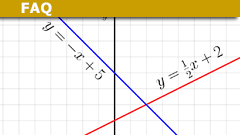
What is a Linear Equation? A 5 Minute Introduction

Definition/Summary

A first-order polynomial equation in one variable, its general form is $Mx+B=0$ where x is the variable. The quantities M, and B are constants and $M\neq 0$.

Equations

$$Mx+B=0$$

Extended explanation

Since $M\neq 0$ the solution is given by

$$x=-B/M\;.$$

The variable x does not have to be a number. For example, x and B could be vectors and M could be a matrix.

In this case, the condition for a solution to existing is

$$\det(M)\neq 0\;,$$

and the solution is given by

$$\vec x = -M^{-1}\vec B\;,$$

where $M^{-1}$ is the matrix inverse of M.

Another (more abstract) example, is Green’s function equation for the time-dependent Schrodinger equation. In this case, x is a Green’s function, and B is a (Dirac) delta function in time, and M is the operator

$$M=\left(\frac{i}{\hbar}\frac{\partial}{\partial t}-\hat H\right)\;,$$

where $\hat H$ is the hamiltonian.

As of linear operators, see also

https://www.physicsforums.com/insights/hilbert-spaces-relatives/
https://www.physicsforums.com/insights/tell-operations-operators-functionals-representations-apart/

 

Comment Thread