Condition Definition and 587 Threads
-
T
Undergrad No Slip condition in an Inviscid Fluid
In an Inviscid fluid would the no slip condition exist? If it didn't would it follow that the free stream velocity would exist at the wall ?. If this was the case would surface roughness still present an orthogonal area upon which the kinetic energy of the fluid would interact causing a... -

Condition of the charge density of atom
Homework Statement Homework EquationsThe Attempt at a Solution ##\rho = b r \\E =\frac { k r^2} {4ε_0} \\ p ∝ E^a \\E \left ( r=d \right ) = \frac { k d^2} {4ε_0} \\ p = q d \\ d ∝ d^{2a} \\a = ½ \\p ∝ √E ## PART B ##\rho ∝ r^n \\E ∝r^{n+1} \\ p ∝ E^a \\d ∝d ^{{n+1}a} \\## For eq. 4.1 to...- Pushoam
- Thread
- Atom Charge Charge density Condition Density
- Replies: 12
- Forum: Introductory Physics Homework Help
-
A
Why Set the Inner Boundary Condition to -1 in Radial Flow Equations?
Hello gents, Q:/ what is the reason for letting the inner boundary condition = (-1) when solving the radial flow of infinite form of diffusivity equation, and i would like to know what will happened if i didn't equate it with (-1). as in the attached pic: https://i.imgur.com/AVesmHM.png- Aows
- Thread
- Boundary Boundary condition Condition Initial conditions
- Replies: 12
- Forum: General Engineering
-
A
Implementing symmetry boundary condition for the diffusion equation
The following lines of codes implements 1D diffusion equation on 10 m long rod with fixed temperature at right boundary and right boundary temperature varying with time. xsize = 10; % Model size, m xnum = 10; % Number of nodes xstp =...- Atr cheema
- Thread
- Boundary Boundary condition Boundary value problem Condition Diffusion Diffusion equation Implicit differentiation Symmetry
- Replies: 4
- Forum: Programming and Computer Science
-

Hausdorf space condition problem
Homework Statement Show that X is a Hausdorff space IFF the 'diagnol of x' given by t = {(x,x) | X * X} is closed as a subspace of X*X Homework EquationsThe Attempt at a Solution So since X Is Hausdorff so is X*X and t, because the product of two Hausdorff spaces if Hausdoff and the subspace...- PsychonautQQ
- Thread
- Condition Space
- Replies: 11
- Forum: Calculus and Beyond Homework Help
-

Graduate Resonance condition of a cyclotron.
the charged particle undergoes acceleration because of the presence of electric field between the two Dee. as a result the electric field needs to change it's direction according to the motion of the charged particle. since the time period of the charged particle does not depend upon the...- esha
- Thread
- Condition Cyclotron Resonance
- Replies: 1
- Forum: Electromagnetism
-
T
How electric potential boundary condition works
Homework Statement [/B] Inside a sperical dielectric mass there is a electric dipole on the center of the sphere. The sphere has radius a. This dieletric sphere is inside and on the center of a conductive spherical shell of radius b. The problem asks to find the potentials and then the...- tomasg
- Thread
- Boundary Boundary condition Condition Conditions Electric Electric potential Potential Works
- Replies: 5
- Forum: Introductory Physics Homework Help
-

Static structural ansys, rigid body boundary condition
hi guys, i am new user on ansys i have task from my lecturer. it is about static test for seat bus. i try simulate the seat bus on ansys statistical structural. you can see my model on attachment (untitle1.png). at that picture, there are 2 bars will push the seat back. the stiffness beahvior...- syamsul
- Thread
- Ansys Body Boundary Boundary condition Condition Rigid body Static Structural
- Replies: 5
- Forum: Mechanical Engineering
-
J
How is Bragg's Law Derived Using the Diffraction Condition?
Hello. I am reading "Introduction to Solid State Physics" by Kittel and there is a derivation in the textbook that I am understanding. This should be a fairly simple question but I am unable to see it. 1. Homework Statement In Chapter 2, it derives the Bragg law using the diffraction condition...- James Marquez
- Thread
- Bragg Condition Diffraction Law Solid state physics
- Replies: 1
- Forum: Advanced Physics Homework Help
-
B
Zangwill, problem 10.19 - A Matching condition for the vector potential A
Homework Statement Show that the normal derivative of the coulomb gauge vector suffers a jump discontinuity at a surface endowed with a current density K(\vec r_s ) Homework Equations The vector potential A is given by: A=\frac{\mu_0}{4\pi}\int{\frac{J(x')}{|x-x'|}d^3x} The magnetic...- BearShark
- Thread
- Condition Potential Vector Vector potential
- Replies: 1
- Forum: Advanced Physics Homework Help
-
T
Undergrad Can Born Rigid Motions Occur in Curved Spacetime?
Can a sphere or disk rotating with uniform speed follow born condition of rigidity?- Tahmeed
- Thread
- Condition Special relativity
- Replies: 8
- Forum: Special and General Relativity
-

Graduate Implementing a weird-looking boundary condition (PDE/FDM)
So I have this problem, taken from Kraus's heat transfer book. So deriving the computational molecule, the conditions for (3.251a), (3.251b) is a bit of a no brainer. The issue I am having is about the boundaries for (3.251c) and (3.251d). This is actually the first time I have seen this...- maistral
- Thread
- Boundary Boundary condition Condition
- Replies: 8
- Forum: Differential Equations
-
J
Condition for condensation from adiabatic expansion
Homework Statement I'm stuck on part (c) of this question. Homework Equations $$T\frac{d}{dT}\bigg(\frac{L}{T}\bigg) \equiv \frac{dL}{dT} - \frac{L}{T}.$$ Clausius-Clapeyron equation: $$ \frac{dp}{dT} = \frac{L}{T\Delta V} \approx \frac{L}{TV_{vap}}.$$ The Attempt at a Solution My approach...- jek8214
- Thread
- Adiabatic Adiabatic expansion Condensation Condition Expansion Gases Phase transitions Thermodynamics
- Replies: 1
- Forum: Advanced Physics Homework Help
-

Graduate Necessary and sufficient condition for an electron to radiat
What is the necessary and sufficient condition for an electron to radiate? How many methods to cause an electron to radiate?- qnach
- Thread
- Condition Elecrtomagnetism Electron Radiation
- Replies: 3
- Forum: Electromagnetism
-

Graduate Deriving functions relating to condition numbers
I have a question stating to derive the functions x |-> f_1(x)=x^3 and f_2(x)=thirdrootof(x) on their domains of definition based on the asymptotic relative condition number KR = KR(f,x). I'm not sure where to start with this question, I'm not sure if I even understand it. Do I find the... -
E
Condition satisified when the body does not slide
Homework Statement A sledge of mass m1 is pulled horizontally with a force F. On the sledge there is a body of mass m2 that can slide on the horizontal platform of the sledge with the friction coefficient μ. Another sledge of mass m3 is tied with a horizontal string of the body m2. Between the...- Eugen
- Thread
- Body Condition Friction Tension
- Replies: 4
- Forum: Introductory Physics Homework Help
-

How to check the condition of coil in the relay?
I am using the relay as chatter. That is I am continuously on-off the relay to produce bursts. I am using 12V DC relay. I got voltage upto ~120V while it is switching very fast initially. Now I am not getting high voltage while switching. I am getting only ~10V. What may be the reason? Is it...- Nikhil N
- Thread
- Coil Condition Relay
- Replies: 4
- Forum: Electrical Engineering
-
B
Finding a Function Given a Condition
Homework Statement I am interested in working on this problem: https://www.physicsforums.com/threads/unknown-composite-function.902469/ From I gather, it seems this problem has been solved already. I was considering joining the thread, but I didn't want to flood songoku's inbox; so I started a...- Bashyboy
- Thread
- Condition Function
- Replies: 7
- Forum: Precalculus Mathematics Homework Help
-

Undergrad Help Solving an Equation with a Boundary Condition
Hello everybody. I'm about to take a final exam and I've just encountered with this exercise. I know it's simple, but i tried solving it by Separation of variables, but i couldn't reach the result Mathematica gave me. This is the equation: ∂u/∂x = ∂u/∂t Plus i have a condition...- FranciscoSili
- Thread
- Boundary Boundary condition Condition Partial differential equations Pde
- Replies: 1
- Forum: Differential Equations
-
I
Find locus of points near ellipse with some condition
Homework Statement Given an ellipse ##\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1## , where ##a \ne b##, find the equation of the set of all points from which there are two tangents to the curve whose slopes are (a) reciprocals and (b) negative reciprocals Homework Equations Equation of a tangent...- issacnewton
- Thread
- Condition Ellipse Points
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
V
Boundary condition for electrostatics problem - found issue?
Hey everyone Just a picture of my configuration. The assumption here is $$\epsilon_a,\epsilon_b,\epsilon_c$$ are different from one another. Really the interest of this problem is to find the scalar potential $$\phi$$, such that $$\nabla^2 \phi = 0$$. So now my question, about jump...- vogtster
- Thread
- Boundary Boundary condition Condition Elecrostatics Electromagnatism Electrostatics Maxwell equations
- Replies: 5
- Forum: Electrical Engineering
-

Graduate Symplectic Condition For Canonical Transformation
I am reading Chapter 9 of Classical Mech by Goldstein.The symplectic condition for a transformation to be canonical is given as MJM' = J, where M' is transpose of M. I understood the derivation given in the book. But my question is : isn't this condition true for any matrix M? That is it doesn't...- CassiopeiaA
- Thread
- Canonical transformation Classical mechanics Condition Symplectic Transformation
- Replies: 3
- Forum: Beyond the Standard Models
-
Graduate What is the purpose of applying a Dirichlet boundary condition?
Hi, If the dirichlet boundary condition is being applied, what does it tell us?- bluejay27
- Thread
- Boundary Boundary condition Condition
- Replies: 1
- Forum: Quantum Physics
-

Graduate Boundary condition for dielectric sphere
Is the potential across the boundary continuous for a dielectric sphere embedded in a dielectric material, so that the potential inside the sphere can be set equal to the potential outside of it at r=R ?- lonewolf219
- Thread
- Boundary Boundary condition Condition Dielectric Potential Sphere
- Replies: 2
- Forum: Electromagnetism
-
P
High School What is a homogeneous boundary condition?
What is a homogeneous boundary condition? Or, more explicitly, what would make a boundary condition inhomogeneous Many thanks :)- Physgeek64
- Thread
- Boundary Boundary condition Condition Homogeneous
- Replies: 1
- Forum: Other Physics Topics
-
J
Undergrad Extremal condition in calculus of variations, geometric
Hi folks, I am a bit confused with the extreme condition used in the calculus of variations: δ = 0 I don't understand this rule to find extreme solutions (maximum or minimum) If in normal differential calculus we have a function y = y(x) and represent it graphically, you see that at the... -
T
Graduate No slip condition in an ideal fluid- Perpendicular pressure
The no slip condition has been described as the adhesion of a fluid to a solid surface setting the relative fluid velocity to zero - cohesion (viscous stress) between fluid elements spreads evenly the velocity gradient through the boundary to the free stream. This also infers that the pressure... -
D
Condition to not let the block descend
Homework Statement In the system shown in Fig. ##2E.5 (a)##. block ##m_2## is being prevented from descending by pulling ##m_1## to the right with force ##F##. Assuming all the surfaces to be frictionless, Find ##F## Homework Equations F.B.D of ##m_1## From the F.B.D of ##m_1## we get the...- decentfellow
- Thread
- Block Condition Newtonian mechanics Pulley
- Replies: 13
- Forum: Introductory Physics Homework Help
-
G
MHB What is the Optimality Condition for a Firm's Profit Maximization Problem?
If I'm given a firm's production function of $$Y=zK^{\alpha}{N}^{1-\alpha}$$ Then assuming $$K$$ is fixed and cost free, we can get our profit maximzation problem of $$\max_{{N}}zF(K^{\alpha}{N}^{1-\alpha})-wN$$ To find the optimality condition, $${MP}_{N}=w$$ , I take the partial...- Ginnee
- Thread
- Condition
- Replies: 1
- Forum: General Math
-
K
Undergrad Is Cauchy Reimann condition sufficient for complex differentiability?
Hi, I have a question about Cauchy Reimann equation lets say z=x+yi is in R^2 And there exists f:R^2->R^2 f(z)=u(x,y)+v(x,y)i Then cauchy reimann condition states that If partial x of f and y of f are equal, then f is holomorphic However, I am not sure how this can be a necesary sufficient...- kidsasd987
- Thread
- Cauchy Condition
- Replies: 4
- Forum: Calculus
-
S
What is the condition in unbounded oprerators?
Homework Statement T1, T2 and T3 are unbounded operators. What is this condition? http://T1 3. The Attempt at a Solution [/B] T2 is the identity operator and D(T3)⊂D(T1) / D is the domain of definition.- smati
- Thread
- Condition
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

Mechanical Boundary condition of a Floating Structure
Dear all, I made a cad of floating structure (the frame only), figure attached below. It should be located in the water and moored, so it can't go anywhere. The CFD simulation was done. So I have fluid force on the structure. Now I want to do mechanical analysis of the structure by apply the...- shade rahmawati
- Thread
- Boundary Boundary condition Condition Floating Mechanical Structure
- Replies: 3
- Forum: Mechanical Engineering
-
D
Looking for an explanation of a simple Lipshitz condition
Homework Statement Has solution It then goes on to state the solution blows up at , which I understand. My issue is when I do the solution I get (Working)- dynamicskillingme
- Thread
- Condition Explanation
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
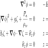
Graduate What are the boundary conditions for rotational flow?
Hello everyone, The boundary condition : P=0, z=ζ is very common when studying irrotational flows. When cast with the Bernoulli equation, it gives rise to the famous dynamic boundary conditionn, which is much more convenient : ∂tφ+½(∇φ)2+gζ=0, z=ζ But what happens if the motion is rotational ...- surfwavesfreak
- Thread
- Bernoulli equation Boundary Boundary condition Condition Fluid mechanics Ocean wave
- Replies: 7
- Forum: Mechanics
-
S
Undergrad Doubts on wavefunction conditions
I'm facing some difficulties in using "boundary conditions" in a simple wavefunction. The wavefunction I'm considering is $$\xi(x,t)=A sin (k x \pm \omega t +\psi)$$ The minus or plus are for progressive or regressive waves. The indipendent parameters are 4: ##A##, ##k##, ##\omega##, ##\psi##...- Soren4
- Thread
- Amplitude Condition Conditions Doubts Frequency Wave Wavefunction
- Replies: 4
- Forum: Quantum Physics
-
K
Undergrad Complex Analysis holomorphic condition
I understood the holomorphic condition this way. For a vector field F(x1, x2 . . ., xm) = <y1(x1, x2, x3 . . . , xm), y2(x1, x2, x3 . . . , xm), y3(x1, x2, x3 . . . , xm) . . . ,yn(x1, x2, x3 . . . , xm)> In a real analysis, its derivative is expressed as a Jacobian matrix because each...- kidsasd987
- Thread
- Analysis Complex Complex analysis Condition
- Replies: 13
- Forum: Topology and Analysis
-
F
No Slip Condition: Which is Correct? Explained
Homework Statement i was told that For a given fluid the velocity of fluid in contact with with solid boundary is equal to the velocity of solid boundary in a book . In another book , I was told that the velocity of fluid at the solid boundary is 0 , which is correct ? can someone explain...- foo9008
- Thread
- Condition Slip Slip condition
- Replies: 1
- Forum: Introductory Physics Homework Help
-
V
Undergrad Is this condition for infinite roots wrong?
I found a strange theorem and a doubtful method in Stroud's book "Engineering mathematics": I think, every polynomial equation will have two infinite roots (at +infinity and -infinity). I also think that this method of the determination of an asymptote gives wrong results if f(x) is a...- vopros217
- Thread
- Condition Infinite Roots
- Replies: 4
- Forum: General Math
-

Undergrad Condition on vector field to be a diffeomorphism.
Hi everybody, Let V(x) a vector field on a manifold ( R^2 in my case), i am looking for a condition on V(x) for which the function x^µ \rightarrow x^µ + V^µ(x) is a diffeomorphism. I read some document speaking about the flow, integral curve for ODE solving but i fail to find a generic...- kroni
- Thread
- Condition Diffeomorphism Field Vector Vector field
- Replies: 3
- Forum: Differential Geometry
-
R
Graduate Valve closure boundary condition
does anyone know what the boundary condition is for a closing valve using the wave equation pde?- rppearso
- Thread
- Boundary Boundary condition closure Condition Valve
- Replies: 1
- Forum: Differential Equations
-
L
Graduate Is the Inner Product in Quaternionic Vector Spaces Truly Hyperhermitian?
Let ##V## be a quaternionic vector space with quaternionic structure ##\{I,J,K\}##. One can define a Riemannian metric ##G## and hyperkahler structure ##\{\Omega^{I},\Omega^{J}, \Omega^{K}\}##. Do this inner product $$\langle p,q \rangle :=...- Leditto
- Thread
- Condition Differential geometry Inner product Symplectic Topology
- Replies: 5
- Forum: Differential Geometry
-
P
Automotive Optimize Feul consubtion, efficiany and slip condition
Hi, I'm working on a wheel loader task and my mission is to optimize the feul consumbtion and controlling the slipp using a appropriate optimal control method. All data is from the tires and I have to by some method tell the motor how much it has to give to machine to drive. Anyone suggest a...- Payam30
- Thread
- Condition Optimal control Slip Slip condition
- Replies: 1
- Forum: Mechanical Engineering
-
C
Graduate Q: Scalar Boundary Condition & U(1) Isometry - Lewkowycz & Maldacena
I have a simple question about Lewkowycz and Maldacena's paper http://arxiv.org/abs/1304.4926v2'][/PLAIN] http://arxiv.org/abs/1304.4926v2 In section 2, they consider the scalar field in BTZ background ground and require boundary condition of the scalar field, $\phi \sim e^{i\tau}$ . This...- craigthone
- Thread
- Black hole Boundary Boundary condition Condition Isometry Quantum field theory Scalar
- Replies: 1
- Forum: Special and General Relativity
-

When Are Two Vectors Orthogonal in Vector Algebra?
Homework Statement Vector u, v, and x are not zero. Vector u + v will be perpendicular (orthogonal) to u-x if A. |u+v| = |u-v| B. |v| = |x| C. u ⋅ u = v ⋅ v, v = -x D. u ⋅ u = v ⋅ v, v = x E. u ⋅ u = v ⋅ v Homework Equations u⋅v = |u||v| cos θ The Attempt at a Solution [/B] Two vectors are...- terryds
- Thread
- Condition Orthogonal Vector
- Replies: 4
- Forum: Precalculus Mathematics Homework Help
-

C/C++ C++ matrix boundary condition problems
I have created a matrix with a class called Lattice. The lattice is filled with objects of type 'Dipole' which is created with another class. The problem I am having is with boundary conditions when I look for a neighbour. e.g If i pick a dipole on the top row, I want its 'above' neighbour to be...- rolotomassi
- Thread
- Boundary Boundary condition C++ Condition Matrix
- Replies: 3
- Forum: Programming and Computer Science
-
M
Non-slip condition for inviscid fluids
Hi, I would like to ask that whether or not ## non-slip condition## is valid for inviscid fluids. We know that inviscid fluids there is no friciton. If there is no friction in the inner surface of pipe (I do not name its technical name) so it seems that there cannot be the non-slip condition...- mech-eng
- Thread
- Condition Fluid mechanics Fluids
- Replies: 4
- Forum: Mechanical Engineering
-
Questions regarding the condition of a buried body
Hello everyone! I'm new to this site, and I'm looking for some help regarding a short story that I'm writing, specifically about the condition of bones (and the remains of a brain) that have been buried for about 5-7 months. I've seen a similar thread, but it didn't really answer my questions...- Kelsey Clifton
- Thread
- Body Condition Death
- Replies: 1
- Forum: Biology and Medical
-
G
Find a function with given condition
Homework Statement Find a curve that passes through point A(2,0) such that the triangle which is defined with a tangent at arbitrary point M, axis Oy and secant \overline{OM} is isosceles. \overline{OM} is the base side of a triangle. 2. The attempt at a solution Function passes through point...- gruba
- Thread
- Analytic geometry Calculus Condition Function Ordinary differential equation
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

Undergrad Basic question, harmonic coordinate condition algebra
where ##□=\nabla^{\mu}\nabla_{\mu}## is the covariant D'Alembertian. ##□x^{\mu}=0## ##g^{\rho\sigma}\partial_{\rho}\partial_{\sigma}x^{\mu}-g^{\rho\sigma}T^{\lambda}_{\rho\sigma}\partial_{\lambda}x^{\mu}=0## So this line is fine by subbing in the covariant derivative definition and lowering...- binbagsss
- Thread
- Algebra Condition Coordinate Harmonic
- Replies: 6
- Forum: Special and General Relativity
-
T
Sketching a graph that meets given condition
Homework Statement Sketch the graph of a function f that is defined on [0,1] and meets the given conditions (if possible) - f is continuous on (0,1), takes on only two distinct values. Homework EquationsThe Attempt at a Solution...- The Subject
- Thread
- Condition Function Graph
- Replies: 4
- Forum: Precalculus Mathematics Homework Help