Derivatives Definition and 1000 Threads
-

Undergrad Directional Derivatives and Derivations - Tangent Spaces
I am reading John M. Lee's book: Introduction to Smooth Manifolds ... I am focused on Chapter 3: Tangent Vectors ... I need some help in fully understanding Lee's conversation on directional derivatives and derivations ... ... (see Lee's conversation/discussion posted below ... ... ) Lee...- Math Amateur
- Thread
- Derivations Derivatives Tangent
- Replies: 4
- Forum: Differential Geometry
-
N
Using Partial Derivatives to estimate error
Homework Statement [/B] The area of a triangle is (1/2)absin(c) where a and b are the lengths of the two sides of the triangle and c is the angle between. In surveying some land, a, b, and c are measured to be 150ft, 200ft, and 60 degrees. By how much could your area calculation be in error if...- Nikstykal
- Thread
- Derivatives Error Estimate Partial Partial derivatives
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
H
Undergrad What is the smoothness condition in vector calculus derivatives?
I'm learning vector calculus and am wondering how general it is. The appear to be using a smoothness condition, but what is it? Certainly the functions are required to have two derivatives. That is, the partial derivatives can be taken twice. Are they further required to have an infinite...- Hornbein
- Thread
- Calculus Condition Derivatives Vector Vector calculus
- Replies: 15
- Forum: Differential Geometry
-

Partial Derivatives. Did I make a mistake or my professor
Homework Statement the equation is E= k((xy)x[hat] +(2yz)y[hat] +(3xz)z[hat]) Homework Equations partial of x with respect to y on the x component partial of y with respect to x on the y component The Attempt at a Solution my professor said during class that the partial of x with respect to y...- grandpa2390
- Thread
- Derivatives Mistake Partial Partial derivatives Professor
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-

The End of the Ski Jump - Optimizing Launch Angle
Homework Statement A ski jumper leaves the ski track moving in the horizontal direction with a speed of 25.0 m/s as shown in Figure 4.14. The landing incline below her falls off with a slope of 35.0°. Where does she land on the incline? I've attached an image of the problem, my work is below...- Bdhillon1994
- Thread
- Angle Derivatives Jump Launch Launch angle Optimization Physics Projectile motion Range
- Replies: 9
- Forum: Introductory Physics Homework Help
-

Graduate Do these two partial derivatives equal each other?
take the function f(x,y,z) s.t dF=(d'f/d'x)dx+(d'f/d'y)dy+(d'f/d'z)dz=0 where "d'" denotes a curly derivative arrow to show partial derivatives Mod note: Rewrote the equation above using LaTeX. $$df = (\frac{\partial f}{\partial x} ) dx + (\frac{\partial f}{\partial y} ) dy + (\frac{\partial...- thegirl
- Thread
- Derivatives Partial Partial derivatives
- Replies: 4
- Forum: Differential Equations
-

Graduate When do total differentials cancel with partial derivatives
I've just done a derivation and had to use the following u_{b}u^{c}\partial_{c}\rho = u_{b}\frac{dx^{c}}{d\tau}\frac{\partial\rho}{\partial x^{c}} = u_{b}\frac{d\rho}{d\tau} We've done this cancellation a lot during my GR course, but I'm not clear exactly when/why this is possible. EDIT: is...- sunrah
- Thread
- Derivatives Differentials Partial Partial derivatives
- Replies: 4
- Forum: Special and General Relativity
-

Proving the Existence of a Single Real Root Using Derivatives
Homework Statement the original function is ##−6 x^3−3x−2 cosx## ##f′(x)=−2x^2−3+2sin(x)## ##−2x^2 ≤ 0## for all x and ##−3+2 sin(x) ≤ −3+2 = −1##, for all x ⇒ f′(x) ≤ −1 < 0 for all x The Attempt at a Solution this problem is part of a larger problem which says there is a cubic...- REVIANNA
- Thread
- Application Derivative Derivatives Mean value theorem
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
M
Interpreting derivatives at a point
Homework Statement How should I interpret the derivative of the following function at C=6% ##N = \frac {I} {C} - D##Homework Equations ## \frac {dN} {dC} = \frac {-I} {C^2} ## At I =12 and C=6%, I am getting ## \frac {dN} {dC} = 3,333 ## I am not sure what to make of this large number. I...- musicgold
- Thread
- Derivatives Point
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-
B
MHB How to Simplify Derivatives Using Common Denominators
Folks, Just struggling to see how this is simplified. \frac{f''(x)}{((1+f'(x)^2)^{1/2}}-\frac{f'(x)^2 f''(x)}{((1+f'(x)^2)^{3/2}}=\frac{f''(x)}{((1+f'(x)^2)^{3/2}} if we let a=(1+f'(x)^2)^{1/2} then I get as far asf''(x)[a^{-1/2}-f'(x)^2a^{-3/2}]=f''(x)[a^{-1/2}-f'(x)^2 a^{-1/2} a^{-1}]... -
X
Expressing A Quantity In Polar Coordinates?
Homework Statement Express the quantity ∂2/∂x2+∂2/∂y2 in polar coordinates. Homework Equations x=ρcosφ y=ρsinφ ρ=sqrt(x2+y2) The Attempt at a Solution This is my first post, so I apologize for any weird looking equations, etc. I know that this is not a difficult problem, but I just cannot...- Xerxesshock2
- Thread
- Calculus Coordinates Derivatives Differentials Modern physics Physics Polar Polar coordinates Quantum
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
C
Find velocity and acceleration using derivatives
Homework Statement we know that the simple armonic motion is characterized by x(t)=Acos(wt), find velocity and acceleration of s.h.m. using derivatives. Homework EquationsThe Attempt at a Solution i should find derivatives of the component of the vector R (Rcos(wt),Rsin(wt)).- carlotta5b
- Thread
- Acceleration Derivatives Physics Velocity
- Replies: 2
- Forum: Introductory Physics Homework Help
-
K
High School Derivatives in Halliday's physics book?
(sorry my bad english). I was reading a Halliday's book of phyisics awhat I found is below. d(72t²)/dt = 144t why did the result was 144? It has anything to do with the deltas in the equation (d and dt)? and second I don't realize why the result of this another equation is this 4t²+2t+3 = 8t+2- kent davidge
- Thread
- Book Derivatives Physics Physics book
- Replies: 6
- Forum: Calculus
-
M
Graduate Partial derivatives and chain rule?
F(r,s,t,v) = r^2 + sv + t^3, where: r = x^2 +y^2+z^2 /// s = xyz /// v = xe^y /// t = yz^2 find Fxx i have 2 solutions for this and i am not sure what is the right one the first solution finds Fx then uses formula : Fxx = Fxr.Rx + Fxs.Sx + Fxv.Vx+Fxt.Tx the 2nd solution find Fx then uses the...- mohamed el teir
- Thread
- Chain Chain rule Derivatives Partial Partial derivatives
- Replies: 2
- Forum: Calculus
-
M
Understanding sensitivity of a variable using derivatives
Hi, Please see the attached file. Homework Statement I am trying to figure out K’s sensitivity to x and y. I wish to know which variable K is more sensitive to. Both x and y are positive decimals less than 1. I want to be able to say a 1% increase in y results in a p% change in K. As the...- musicgold
- Thread
- Derivatives Sensitivity Variable
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-

Derivatives in relation to physics
OK, I have never had physics till this semester and I am in calculus based physics and it is kicking my butt. I don't understand how derivatives are properly used in the formulas, and I have an example, my question is the image attached. @=theta A=alpha SO, A) I need omega (angular velocity)...- SadPanda6022
- Thread
- Derivatives Physics Relation
- Replies: 8
- Forum: Introductory Physics Homework Help
-
M
Understanding distances, derivatives, and integrals help?
Homework Statement Two railroad tracks intersect at right angles at station O. At 10AM the train A, moving west with constant speed of 50 km/h, leaves the station O. One hour later train B, moving south with the constant speed of 60 km/h, passes through the station O. Find minimum distance...- Monkey D. Luffy
- Thread
- Derivatives Integrals Kinematics Motion One dimensional motion Trains
- Replies: 4
- Forum: Introductory Physics Homework Help
-
H
Graduate Can B-splines cause oscillations in second derivatives?
Hi, I have been playing with B-splines recently and I have had some curious results. As a rest, I had a set of points on the ellipse; \frac{x^{2}}{9}+y^{2}=1. I used the paramatrisation x=3\cos\theta ,\quad y=\sin\theta and I computed the derivatives numerically (I had to come up with a...- hunt_mat
- Thread
- Derivatives
- Replies: 2
- Forum: General Math
-
Z
Derivatives: Find Q and its tangent
Homework Statement Disclaimer: English is not my first language, so i apologize for any wrong math-terms. We look at the function f(x) = x^3. On the graph for f we have a point, P(a,a^3), where a =/= 0. The tangent to f through P cuts through f in another point, Q. Find Q and show, that the...- zebo
- Thread
- Derivatives Tangent
- Replies: 12
- Forum: Calculus and Beyond Homework Help
-

Graduate Proving equality of mixed second order partial derivatives
Let ##f(x,y)## be a scalar function. Then $$\frac{∂f}{∂x} = \lim_{h \rightarrow 0} \frac{f(x+h,y)-f(x,y)}{h} = f_x (x,y)$$ and $$\frac{∂}{∂y} \left (\frac{∂f}{∂x} \right ) = \lim_{k \rightarrow 0} \frac{f_x(x,y+k)-f_x(x,y)}{k} = \lim_{k \rightarrow 0} \left ( \frac{ \displaystyle \lim_{h... -
Graduate Calculating mixed partial derivatives on a 3D mesh
I am working on implementing a PDE model that simulates a certain physical phenomenon on the surface of a 3D mesh. The model involves calculating mixed partial derivatives of a scalar function defined on the vertices of the mesh. What I tried so far (which is not giving good results), is this...- KareemErgawy
- Thread
- 3d Derivatives Hessian matrix Mesh Mixed Partial Partial derivatives
- Replies: 6
- Forum: Differential Geometry
-

Why aren't the derivatives equal?
Homework Statement Homework Equations see above The Attempt at a Solution After getting ##v = |\frac{dz}{dt}|=\frac{3}{t^2+1}## why can't I simply take the derivative of that with respect to ##t## to get the acceleration? ]- Calpalned
- Thread
- Derivatives
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-

Undergrad Gradients vs. Partial Derivatives
What is the difference between partial derivatives and gradients, if there is any? I'm asking because I need to derive a function " f (T,P) " for air convection; where T is temperature and P is pressure and both are variables in this case. Thanks- shanepitts
- Thread
- Derivatives Partial Partial derivatives
- Replies: 3
- Forum: Calculus
-
F
Applications of Partial Derivatives
Homework Statement Let l, w, and h be the length, width and height of a rectangular box. The length l is increasing with time at at rate of 1 m/s, while the width and the height are decreasing at rates 2 m/s and 1m/s respectively. At a certain moment in time the dimensions of the box are l=5...- FuturEngineer
- Thread
- Applications Derivatives Partial Partial derivatives
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
B
Graduate Question about partial derivatives.
I have a multivariable function z = x2 + 2y2 such that x = rcos(t) and y = rsin(t). I was asked to find (I know the d's should technically be curly, but I am not the best at LaTeX). I thought this would just be a simple application of chain rule: ∂2/(∂y∂t) = (∂z/∂x)(ⅆx/ⅆt) + (∂z/∂y)(ⅆy/ⅆt)...- BigFlorida
- Thread
- Derivatives Partial Partial derivatives
- Replies: 3
- Forum: Calculus
-

Graduate Understanding Partial Derivatives in Position-Velocity Relationship
Hi, I'm a little confused about something. I have an object, and I want to take the partial derivative of its position wrt velocity and vice versa. I'm not sure how to begin solving this problem. Essentially, what I have is this: ## \frac{\partial x}{\partial \dot x} ## and ## \frac{\partial... -
N
What Is the Equation of State Given Compressibility and Expansivity Relations?
Homework Statement Find the equation of state given that k = aT^(3) / P^2 (compressibility) and B = bT^(2) / P (expansivity) and the ratio, a/b? Homework Equations B = 1/v (DV /DT)Pressure constant ; k = -1/v (DV /DP)Temperature constant D= Partial derivative dV = BVdT -kVdP (1) ANSWER is...- NucEngMajor
- Thread
- Derivatives Partial Partial derivatives Thermo
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
T
Geometric series and its derivatives
Homework Statement I was browsing online and stumbled upon someone's explanation as to why 1 -2 +3 -4 + 5... towards infinity= 1/4. His explanation didn't make sense to me. He starts with a geometric series, takes a derivative, and plugs in for x = -1, and gets a finite value of 1 -2 + 3 - 4...- thepatient
- Thread
- Derivatives Geometric Geometric series Series
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
S
Time derivatives of polar motion
Homework Statement A particle moves with v=constant along the curve $$r = k(1+\cos \theta)$$Find ##\mathbf{a}## Homework Equations $$ \mathbf{r} = r\mathbf{e_r}$$ $$ \mathbf{v} = \frac{\partial}{\partial t}(r\mathbf{e_r}) $$ $$ \mathbf{a} = \frac{\partial \mathbf{v}}{\partial t} $$...- stumpoman
- Thread
- Derivatives Motion Polar Time
- Replies: 1
- Forum: Advanced Physics Homework Help
-
J
Partial Derivatives: Solve f(x,y)=1,000+4x-5y
Homework Statement Find ∂2f ∂x2 , ∂2f ∂y2 , ∂2f ∂x∂y , and ∂2f ∂y∂x . f(x, y) = 1,000 + 4x − 5y Homework EquationsThe Attempt at a Solution Made somewhat of an attempt at the first one and got 0, however my teacher has poorly covered this in class, and I would value some further explanation.- Julian12345
- Thread
- Derivatives Partial Partial derivatives
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
B
Time derivatives in Spherical Polar Coordinates
Homework Statement Evaluate r(hat and overdot), θ(hat and overdot), φ(hat and overdot) in terms of (θ , Φ) and the time derivatives of the two remaining spherical polar coordinates. Your results should depend on the spherical polar unit vectors. Homework Equations ∂/∂t= The Attempt at a...- Biffinator87
- Thread
- Coordinates Derivatives Polar Polar coordinates Spherical Time
- Replies: 3
- Forum: Advanced Physics Homework Help
-
S
Chain Rule Problem (Partial derivatives)
Homework Statement Homework EquationsThe Attempt at a Solution I have the solution to this problem and the issue I'm having is that I don't understand this step: Maybe I'm overlooking something simple but, for the red circled part, it seems to say that ∂/∂x(∂z/∂u) =...- slr77
- Thread
- Chain Chain rule Derivatives Partial derivatives
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
I
Graduate Commutator of two covariant derivatives
Hello all, I'm trying to calculate a commutator of two covariant derivatives, as it was done in Caroll, on page 122. The problem is, I don't get the terms he does :-/ If ##\nabla_{\mu}, \nabla_{\nu}## denote two covariant derivatives and ##V^{\rho}## is a vector field, i need to compute...- ibazulic
- Thread
- Commutator Covariant Derivatives
- Replies: 5
- Forum: Special and General Relativity
-
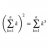
Graduate Sterman's QFT - 2.7b (on functional derivatives)
I've been trying to fill in my mathematical blanks of things I just took as dogma before. Especially, not having a background in functional analysis, the functional derivatives often seem to me mumbo jumbo whenever things go beyond the "definition for physicists". In particular I tried looking...- ddd123
- Thread
- Derivatives Functional Functional analysis Qft
- Replies: 3
- Forum: Quantum Physics
-
Graduate How does the Kalman filter calculate derivatives?
Suppose we have a Kalman filter. We have a position sensor, for example GPS. We use the filter to estimate position. However in all examples I see higher derivatives in the state vector: speed, acceleration and sometimes jerk. There is no sensor that calculates these values directly, so they...- haael
- Thread
- Derivative Derivatives Filter Kalman filter
- Replies: 3
- Forum: General Math
-
M
Graduate Making sense of vector derivatives
Im trying to understand helmholts decomposition, and in order to do so, I feel the need to understand the different ways to apply the del operator to a vector valued function. The dot product and the cross product between two ordinary vectors are easy to understand, thinking about them as a... -
C
Undergrad Derivatives in Action, Change in radius per time of circle.
Hi, I'm trying to understand how Differentiation and integral works in practice, and would really appreciate some help interpreting this calculation- If we have a circle with Area A=pi*r^2 1) If i want to find the change in Area with respect to radius then dA/dr= 2pi*r2) If I'm told...- christian0710
- Thread
- Change Circle Derivatives Per Radius Time
- Replies: 2
- Forum: Calculus
-
C
Undergrad Mixing units with functions or derivatives?
Hi, How do you correctly use units when writing derivatives and functions in math? Example A car goes 17miles per gallon, so a function m with the equation m(g)=17g describes the distance it can go with g gallons. And the derivative dm/dg = 17 miles/gallon. Question: could you write the...- christian0710
- Thread
- Derivatives Functions Mixing Units
- Replies: 4
- Forum: Calculus
-
D
How Do You Derive the Acceleration Function from a Given Velocity Equation?
Homework Statement Derive the function for the acceleration from this function v=√(2P/M)(√T) The answer is √(P/2MT) I have tried many different attempts but I am still unable to reach this answer. [/B] I am sure the process to get to the answer is a simple one but for some reason I am...- david98999
- Thread
- Derivatives Derive Function Mathematics Velocity
- Replies: 4
- Forum: Introductory Physics Homework Help
-
M
Undergrad What Are Examples of Non-Linear Operators in Mathematics?
Hello every one . If the derivative is a linear operator ( linear map ) Then what is the example of non-linear operator Thanks .- mikeeey
- Thread
- Derivatives Intro Non-linear Operators
- Replies: 5
- Forum: Linear and Abstract Algebra
-
C
Covariant derivatives commutator - field strength tensor
Homework Statement So I've been trying to derive field strength tensor. What to do with the last 2 parts ? They obviously don't cancel (or do they?) Homework EquationsThe Attempt at a Solution [D_{\mu},D_{\nu}] = (\partial_{\mu} + A_{\mu})(\partial_{\nu} + A_{\nu}) - (\mu <-> \nu) =...- caimzzz
- Thread
- Commutator Covariant Derivatives Field Field strength Strength Tensor
- Replies: 2
- Forum: Advanced Physics Homework Help
-

Graduate Is There a Defined Method for Calculating Quaternion Derivatives?
I am trying to work out some basic aspects in the theory of quaternions for some work in physics I'm doing. I have went through complex analysis and saw that the only way division ( and hence the derivative) could be defined was through a numerical definition of (i). My question is does there...- Topolfractal
- Thread
- Derivatives Quaternion
- Replies: 5
- Forum: Differential Equations
-
N
Graduate Relation between inequalities for first and second derivatives
Hi, If f'(x) >= f'(y) can we say that f''(x) >= f''(y) also holds ? And if yes under which conditions ? Thanks -
B
MHB How Do You Prove a Vector is Unit Along a Parametric Curve?
Hey everyone, I am given the following function f(x,y) = xy+x+y along the curve x(s)=rcos(s/r) and y(s)=rsin(s/r). I have to show that (dx/s)i + (dy/ds)j is a unit vector. I am unsure where to begin with this :/ Can anyone please give me some hints/ideas on how to approach this question?- brunette15
- Thread
- Derivatives Proof
- Replies: 1
- Forum: Calculus
-
M
MHB Partial Derivatives: Find $\frac{\partial^2{w}}{\partial{u}\partial{v}}$
Hey! :o Let $w=f(x, y)$ a two variable function and $x=u+v$, $y=u-v$. Show that $$\frac{\partial^2{w}}{\partial{u}\partial{v}}=\frac{\partial^2{w}}{\partial{x^2}}-\frac{\partial^2{w}}{\partial{y^2}}$$ I have done the following: We have $w(x(u,v), y(u, v))$. From the chain rule we have... -
S
Graduate Find the function phi(r,t) given its partial derivatives.
I would like to define t^*= \phi(r, t) given dt^* = \left( 1-\frac{k}{r} \right) dt + 0dr where k is a constant. Perhaps it doesn't exist. It appears so simple, yet I've been running around in circles. Any hints?- stedwards
- Thread
- Derivatives Function Partial Partial derivatives
- Replies: 2
- Forum: Differential Equations
-
C
MHB Partial derivatives of the natural logs
Find the partial derivatives of the following function: Q=(1/3)logeL+(2/3)logeK Any help would be much appreciated! Below is my working out so far: \frac{\partial Q}{\partial L}= \frac{\frac{1}{3}}{L} \frac{\partial Q}{\partial K}= \frac{\frac{2}{3}}{L} Are these correct?- claratanone
- Thread
- Derivatives Natural Partial Partial derivatives
- Replies: 1
- Forum: Calculus
-
R
Graduate Derivatives and Linear transformations
Let G be a non-empty open connected set in Rn, f be a differentiable function from G into R, and A be a linear transformation from Rn to R. If f '(a)=A for all a in G, find f and prove your answer. I thought of f as being the same as the linear transformation, i.e. f(x)=A(x). Is this true?- raghad
- Thread
- Complex analysis Derivative Derivatives Linear Linear transformation Linear transformations Transformations
- Replies: 12
- Forum: Topology and Analysis
-

Undergrad Is differentiation a possible approach?
Question: I have a function of time. Its expression has a constant 'b' in it. I am asked to ascertain how changing 'b' affects the function. Specifically, I have velocity as a function of time which accounts for drag forces; 'b' is the drag coefficient. I am asked to ascertain how changing 'b'... -
H
Graduate Proof of equality of mixed partial derivatives
In the proof, mean value theorem is used (in the equal signs following A). Hence, the conditions for the theorem to be true would be as follows: 1. ##\varphi(y)## is continuous in the domain ##[b, b+h]## and differentiable in the domain ##(b, b+h),## and hence ##f(x,y)## is continuous in the...