Learn About the Speed of Light and Galilean Relativity
Table of Contents
Speed of Light Key Points
- Early experiments attempted to measure the speed of light, including Galileo‘s lantern experiment, Ole Rømer‘s eclipse experiment, and James Bradley‘s stellar aberration experiment.
- Hippolyte Fizeau was the first to accurately measure the speed of light with his cogwheel and water experiments.
- The Fizeau water experiment showed that light velocity is not additive with the velocity of its source, as predicted by Galilean relativity.
- The de Sitter double star experiment proposed that if the speed of light were additive with its source, strange effects should be observed in binary star systems. No such effects have been observed.
- The Michelson–Morley experiment found no evidence for a preferred reference frame for the propagation of light, contrary to expectations from the ether theory.
- All these experiments led to the conclusion that the speed of light is constant in all reference frames, giving rise to the formulation of special relativity.
Introduction
In this article, I will discuss some experiments in the 19th and early 20th centuries that looked at how the velocity of a light source affects the speed of the light emitted from it. In particular, the Fizeau water experiment, the de Sitter double star experiment, and the Michelson-Morley experiment, which is the most well-known. These experiments cast significant observational doubt on the Galilean idea of relativity as it applies to light, that the velocities of the emitted light and the source simply add together. We know now that this is wrong and that special relativity must be taken into account, but that was not always the case and had to be inferred from observation.
I will not discuss experiments devised with the hindsight of special relativity (such as measurements of time dilation), although they are interesting. I will also not go into the details of ether theory, because I’m not too familiar with it.
All images in this article are from Wikipedia.
Early Determination of the Speed of Light
The first attempted measurement of the speed of light that I know of was by Galileo himself and an assistant, who stood on opposing hilltops and attempted to communicate by opening a lantern shutter and waiting for the lantern on the opposing hill to be opened in response. They did not notice a delay and concluded that the speed of light must be much faster than the speed of sound. Although this experiment was inconclusive, it was one of the first examples of a negative result being used to constrain the bound of an unknown quantity, an analytical technique so common in physics today.
Diagram of Romer’s observations. The timing of Io’s eclipses is different if the Earth is at H or at E.
The first partially successful measurement was by Ole Rømer who was making careful observations of eclipses of the moon Io by Jupiter’s shadow. He noticed that the eclipses did not appear on a regular schedule as expected, but varied by a few minutes depending on where Earth was for Jupiter in its orbit. He reasoned that this variation was due to the time taken for the light to reach the Earth, and took an extra 22 minutes to cross the diameter of Earth’s orbit if it was farther from Jupiter. This isn’t too far off from the 16 minutes we now know it takes. With an accurate knowledge of the astronomical unit, this puts his speed of light at 222,000 km/s. This is significant because it was the first piece of evidence that the speed of light is finite.
In the 18th century, James Bradley made a measurement of stellar aberration, the apparent change in the position of a star due to the velocity of Earth relative to the star (not to be confused with parallax, which is a change in apparent position due to the changing position of Earth). Based on the 20-arcsecond change in a star’s position due to aberration over a year, he concluded that light must travel about 10,000 times as fast as Earth does around the sun, and was able to conclude that light takes eight minutes to reach the Earth from the sun, even though he didn’t know the speed of light or the astronomical unit.
The first “modern” measurement of the speed of light was in the 1840s by Hippolyte Fizeau. He shone light through the teeth of a quickly rotating cog, off a distant mirror, and back through the cog. If the cog rotated slowly, the light would pass through the same gap. If it was going sufficiently fast, it would be blocked as the tooth would rotate into its path. If it were going even faster, the next gap would rotate into its path and it would get through again. By measuring the amount of light getting through as a function of the cog’s rotational speed, he could measure the speed of light by finding the cog speed that would allow it to get through the next gap. He measured about 313,000 km/s, within 5% of the actual value.
Diagram of Fizeau’s experiment. He presumably did not use a lightbulb, and the mirror was eight kilometers away.
The Fizeau Water Experiment
In addition to his cogwheel experiment, Fizeau did an experiment measuring the speed of light through moving water. Light through water is slower than light in a vacuum, and if the light is “dragged” along with the water then one could naively expect that its velocity would just be the sum of the velocity of the water and the speed of light in the water. To test this, Fizeau designed an experiment where two parallel beams of light were sent through two columns of counter-flowing water, reflected off a mirror, and sent back through the other column of water. One beam of light would always be traveling with the current, and one always against it. The beams were then projected onto the same spot so that an interference pattern could be seen. The magnitude of the interference depends on the relative velocity of the two beams.
Set up from the Fizeau experiment. Light emitted at S is split into two beams at G, through two slits at E, and through tubes of water in A where it flows in the directions of the arrow. After being reflected at m, the light goes back through the opposite tube of water, and the two beams meet again at G and interfere. One beam is always going with the flow of water, while one is always going against the flow.
The result was not null. However, it did not verify the Galilean dragged light hypothesis. The size of the interference fringe he observed was about half of what was expected. Taking special relativity into account, we can apply relativistic velocity addition to find that the two beams differ in speed by a factor ##1-\frac{1}{n^2}\approx 0.43## times the speed of the water (n is the index of refraction), so the special relativistic effect is roughly half of the Galilean effect. Fizeau wasn’t aware of this derivation, but he could see that the Galilean prediction was wrong by a factor of two.
Looking at an English translation of his initial report, he comments that the observed interference effect is half that of his expectation, but quite close to the “ether drag” theory that the medium of light propagation was dragged along with the water. Again, hindsight is 20/20 but this was a step in the right direction.
The de Sitter Double Star Experiment
This analysis actually took place in the 1910s, after special relativity had been formulated, but conceptually it could have been understood centuries earlier. It was proposed by Willem de Sitter, better known for the eponymous space-time and its arch-nemesis, de Sitter space and anti-de Sitter space.
A diagram of the “experiment,” an observation of an orbiting star at two phases of its orbit, with the assumption that the speed of light is additive.
Consider the light being emitted by one member of a binary star system, with the Earthward velocity of the star oscillating periodically with the orbit. If the speed of the light adds to the speed of the star, it could eventually catch up with the light emitted by the star as it moves away from us in its orbit. If the stars are sufficiently far from Earth, we would observe some strange things as the blue-shifted light caught up with the red-shifted light, including spontaneous duplications of spectral lines, multiple appearances of the same star at a given time, and violations of Kepler’s laws, all of which would be more extreme for more distant stars, as there would be more time for the fast light to catch up with the slow light.
An animation of faster-blueshifted light catching up with slower redshifted light from a member of a binary star system. If both pulses reach Earth at the same time, the image of the star briefly doubles.
Fortunately, we live in a galaxy full of binary star systems, so we can test this. In 1913, none of these effects had been observed (although de Sitter’s paper is a little skimpy on the data), and they still haven’t. If the simple velocity addition of light were true, then to be consistent with observations the laws of orbital mechanics would have to depend on their distance from Earth.
The Michelson-Morley Experiment
This experiment is typically mentioned when introducing special relativity, sort of as an experimental nail of the coffin for ether theory. There’s a lot of mixing and mashing of historical timelines that are rearranged to introduce concepts in a pseudo-chronological order, and it’s not known to what extent Einstein was influenced by it in 1905, as he only credits the Fizeau experiment.
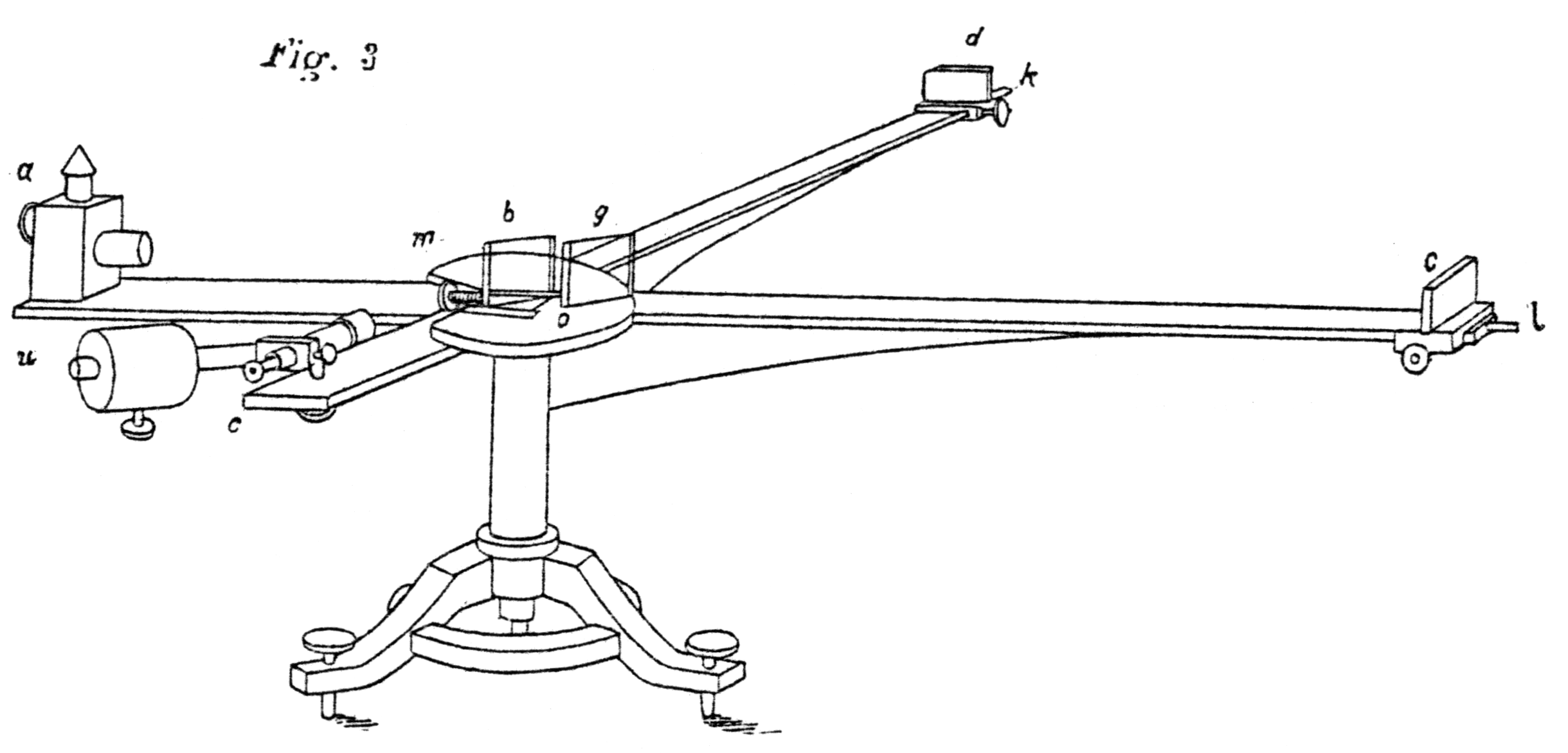
A Michelson interferometer, where light from a is split at b, bounces off the mirrors at d and c, we recombined at q and then observed at e.
The experiment was not so much a refutation of Galilean relativity per se, but rather the idea that there is a fixed reference frame through which light propagates. This experiment was the most sensitive interferometer of its time, spitting two beams of light, sending them along different perpendicular paths, and then reuniting to form an interference fringe. If the speed of light were different in different directions due to the motion of the Earth relative to the rest frame of light propagation, the interference pattern would change. By rotating the entire experiment, they closely probed the relative velocities of light in the two arms relative to Earth’s movement, and they found nothing. Any potential signal that could be observed was less than a fortieth that of the theoretical prediction.
The Michelson-Morley experiment with a preferred light frame. If the entire apparatus, on the orbiting Earth, moves with respect to light’s reference frame, the beams going in perpendicular directions would arrive at different times.
These results, according to my 21st-century physics education, really made people think about a potential rest frame for light and the existence of luminiferous ether. Lorentz developed his transformations to explain this experiment, which fit nicely into special relativity.
Conclusion
All of these experiments probe a fairly simple idea, that the velocity of light is additive with its source. Each of them is fairly straightforward to understand on a conceptual level and doesn’t require special relativity to understand (although it certainly helps in interpreting their results). By considering these experiments, I think one could discount the idea that light’s speed simply adds to the speed of its source, as is required by Galilean relativity, and would force the physicists of the day to dig deeper to uncover the nature of light, which is indeed what happened. Physics students have been told for generations that the speed of light is constant in all rest frames and that that leads to Lorentz transformations, but it’s important to remember how we know that is the case.
Ph.D. McGill University, 2015
My research is at the interface of biological physics and soft condensed matter. I am interested in using tools provided from biology to answer questions about the physics of soft materials. In the past I have investigated how DNA partitions itself into small spaces and how knots in DNA molecules move and untie. Moving forward, I will be investigating the physics of non-covalent chemical bonds using “DNA chainmail” and exploring non-equilibrium thermodynamics and fluid mechanics using protein gels.
Thank you for your reply. I love Heidelberg especially the castle. My sons played with the Waldorf Astoria team. I think I got it now. I had not read the Maxwell equations. Still learning Physics speech.
It's a bit late, but I missed this reply. In my language they have the saying "better sometime than never", so here it goes.
Can you be more explicit? I wasn't aware that there was such a thing. Maxwell's equations are Maxwell's equations; they are Lorentz invariant, not Galilean invariant.My point was, that when you want to consider elecotromagnetism in the non-relativistic limit (such that you obtain equations that are Galilei-covariant), the time derivatives of both fields drop out. Levy-Leblond (Nuovo Cimento B 14, 217-234) showed that these equations correspond to the limit c –> oo of the Maxwell equations. For an arxiv-link, see e.g.
https://arxiv.org/abs/1303.5608
Very enjoyable read. Now have to go think again.:-)
[QUOTE="Laurie K, post: 5618904, member: 578188"]The diagrams are not of world lines but more like the Optical Appearance plot used by Øyvind Grøn in the Fig 9 part C plot in his paper "Space geometry in rotating reference frames: A historical appraisal". http://areeweb.polito.it/ricerca/relgrav/solciclos/gron_d.pdf“This does not change the fact that calling them photon paths is a huge misnomer.
[QUOTE="Orodruin, post: 5618197, member: 510075"]Actually, calling the world line of a classical massless particle in SR a "photon path" is a huge misnomer.”The diagrams are not of world lines but more like the Optical Appearance plot used by Øyvind Grøn in the Fig 9 part C plot in his paper "Space geometry in rotating reference frames: A historical appraisal". http://areeweb.polito.it/ricerca/relgrav/solciclos/gron_d.pdf
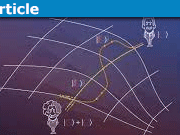
[QUOTE="vanhees71, post: 5618188, member: 260864"]Whatever is shown in your diagrams are no photon paths. There is not even a position observable for photons. Maybe it shows "light rays" in the proper sense of the eikonal approximation, but that must not be thought of as "photon trajectories".”I was originally wondering how a simple geometric rotating observational model would work on galactic scales and if the apparent changes in shift along the way could appear within the optical Depth of Field of our astronomical observations. This is how the light rays, if you like, were plotted for the 45 degree plot vanhees71. The observer is at the point where the photons arrive after one complete rotation of the source(s) and the 'light rays' shown are for the photons still in transit between the source(s) and the observer. After one quarter of rotation photons from the start point 1,0 have travelled directly towards the observer and reach point 1, 1 while their source moves to position 4,0. Accordingly the photons emitted from start point 3,0 travel to point 3,1 while their source moves to point 2,0. All other photons emitted from their sources (heading directly towards the observer) are spread between points 4,0 & 1,1 and 2,0 & 3,1 respectively.After two quarters of rotation the photons that arrived at point 1,1 have traveled to point 1,2, the photons at 4,0 traveled to point 4,1 and the source has moved to point 3,0 so the newly emitted photons are spread out between 3,0 and 4,1. The photons that arrived at point 3,1 have traveled to point 3,2, the photons at 2,0 traveled to point 2,1 and the source has moved to point 1,0 so the newly emitted photons are spread out between 1,0 and 2,1. After three quarters of rotation the photons at point 1,2 have traveled to point 1,3, the photons at 4,1 traveled to point 4,2, the photons at point 3,0 traveled to point 3,1 and the source is at 2,0. The newly emitted photons are spread out between 2,0 and 3,1. The photons at point 3,2 have traveled to point 3,3, the photons at 2,1 traveled to point 2,2, the photons at point 1,0 traveled to point 1,1 and the source is at 4,0. The newly emitted photons are spread out between 4,0 and 1,1. After one complete rotation the photons at point 1,3 have traveled to the observer at point 1,4, the photons at 4,2 traveled to point 4,3, the photons at point 3,1 traveled to point 3,2, the photons at 2,0 traveled to point 2,1 and the first source is back at its start point 1,0. The newly emitted photons are spread out between 1,0 and 2,1. The photons at point 3,3 have traveled to the observer at point 3,4, the photons at 2,2 traveled to point 2,3, the photons at point 1,1 traveled to point 1,2, the photons at 4,0 traveled to point 4,1 and the second source is back at its start point 3,0. The newly emitted photons are spread out between 3,0 and 4,1.
I try to consistently use the term "light pulse" when I am talking about classical flashes of light. Especially if I am neglecting diffraction and other complications.
[QUOTE="Laurie K, post: 5618177, member: 578188"]That would make it very hard to solve SR based relativistic rolling wheel problems, especially for solutions with "optical appearance" plots.”There is no need to talk about photons in this respect. Just as there is no need to talk about photons when doing classical ray optics. Actually, calling the world line of a classical massless particle in SR a "photon path" is a huge misnomer. See also the reply by vanhees71.
Usually when in wanna-be modern textbooks about classical phenomena photons are used you can as easily also use the more consistent and correct description of classical electrodynamics. What's called a "photon" in such cases is often just "ray optics" (i.e., the eikonal approximation) or just kinematics of the wave-number four-vector ##(k^{mu})=(omega/c,vec{k})##. Whatever is shown in your diagrams are no photon paths. There is not even a position observable for photons. Maybe it shows "light rays" in the proper sense of the eikonal approximation, but that must not be thought of as "photon trajectories".
[QUOTE="Orodruin, post: 5326611, member: 510075"]There is no need to even talk about photons in special relativity, photons are not present.”That would make it very hard to solve SR based relativistic rolling wheel problems, especially for solutions with "optical appearance" plots. [QUOTE="Orodruin, post: 5326611, member: 510075"]Photons are not small billiard balls. Regardless, the events of emission and detection exist in all frames – they are not coordinate dependent. Any other statement borders on misinformation.”I tend to agree with you on this one. Have you ever wondered what happens, 'optical appearance' wise, between emission and detection in a de Sitter double star type experiment with a constant c? The following diagram shows the photon paths, emitted from 2 rotating sources, that travel directly to an observer at c over one complete rotation. These photons exist at the time of the observation as long as the sources continued to emit during the previous complete rotation and the emitted photons were not blocked or distorted. The observation point is stationary wrt to the center of the sources plane of rotation and the photon paths are shown for the observer being at various different angles 0, 45, 60, 90 degrees to the plane of rotation. The color of the paths reflects the shift at the point of emission, for each quarter, which is then kept consistent as the photon travels through to the observer. The speed of light is kept constant because the distance between the 2 emission start points 1,0 3,0 and the observer will always be the same regardless of the angle of the observer to the plane of rotation of the sources or the angular velocity of the sources themselves. This distance will always equal 2 * Pi * r * c/v after one complete rotation of the sources for both sources angular velocities<c.
In the section on de Sitter's experiment, there is a trivial typo, "more extreme for more distance stars" should be "more distant stars".The possibility of the speed of the source adding to the speed of the light was proposed by Ritz, as I remember in 1908, as an alternative explanation for the Michelson-Morley experiment but I'm not sure if that was part of de Sitter's motivation.
[QUOTE="exmarine, post: 5326593, member: 106947"]Any photon that one sees apparently arrives with velocity c. … I don't think one can detect a photon destined to be observed in some other reference frame.”I would suggest you think carefully about how one could determine the speed of arrival from a single event, namely the detection of the photon.
Interesting ideas, but is there a follow-up paper showing that it's consistent with the high-precision results of standard QED, i.e., the usual radiative corrections also predicting, among other things, the vacuum polarization (or photon self-energy)? The directly observable consequences of standard QED radiative corrections are in great agreement with experiment (Lambshift of hydrogen, anomalous magnetic moment of the electron; some quibbles for the anomalous magnetic moment of the muon due to the more significant QCD corrections), and any (speculative) semiclassical model of vacuum polarization should be at least as precise as the standard QED results!
Here is one of the two papershttps://arxiv.org/abs/1301.3923Edit: and the otherhttps://arxiv.org/abs/1302.6165When they are available on arXiv it is always polite to provide links.
There were 2 papers in the European Phys.J. in March 2016, one by M. Urban et al., the other by Leuchs and Sanchez concerning the effects of virtual particles on c. Also a book by J. Maguegeyo, Faster than the speed of light:The story of a scientific speculation, Basic Books, 2003 dealing with a higher c in the early universe.
[QUOTE="nettleton, post: 5616394, member: 601270"]I have read a couple of papers, which have been subject to criticisms, that c may vary via its interactions with virtual particles in space.”Please give a specific reference. We can't answer your question without knowing what specific papers you have looked at.
I am puzzled why c is defined as the velocity of light in presumably a perfect vacuum. I have read a couple of papers, which have been subject to criticisms, that c may vary via its interactions with virtual particles in space. Is there an accepted theory dealing with the effect of variation in the number densities in space through which light propagates?
“How do you explain the The Fizeau Water Experiment which demonstrates 3 inertial frames being observed having 3 different speeds relative to each other?
“Some interesting points of discussion have been brought up, some of which you are discussing amongst yourselves. I will attempt to address the questions asked to me directly.
Regarding Fizeau’s experiment with the cogwheel, I do not have the original source unfortunately.
“Maxwell’s equations showing that the speed of light propagates with a constant velocity is usually used as the motivation for replacing Galilean relativity with Einstein’s relativity. Where do Maxwell’s equations fit into this picture? Were the scientists motivated by testing his prediction of a constant velocity of light or were they just trying to measure the speed of light as a experimental challenge?”
I think this is where a bit of historical rearrangement comes into it for pedagogical purposes. Many of these experiments took place before Maxwell’s electromagnetic wave equation was derived. The derivation of the speed of light from Maxwell’s equations shows that its speed is related to the magnetic and electric properties of the vacuum, which is interesting, especially so in the 19th century I imagine, but by themselves I don’t see how they imply special relativity unless you already assume that the Lorentz transform is the right way to go between reference frames. To show that the speed is the same in all reference frames you’d have to know that, let’s say, the electric attraction between two charges didn’t depend on how fast they were moving with respect to some fixed frame. We now know that’s true, but that information would have to be input into Maxwell’s derivation somehow, which it normally isn’t.
Regarding the definition of Galilean invariance, I was going with the idea that considering dynamics of ball throwers on a riverboat in the rest frame of the shore by subtracting the speed of the river would also work for people playing laser tag. I guess technically this means that Galilean relativity assumes that the Galilean transformation is the correct way to go between frames, which is an equivalent statement to the ones you pasted.
I am not familiar with Schulenberger’s work.”
If you are genuinely interested in figuring things out about how the universe works, perhaps you should peruse Schulenberger’s little paper. It is brief and to the point: The Michelson-Morley experiment is irrelevant; thus an aether may exist.
Some interesting points of discussion have been brought up, some of which you are discussing amongst yourselves. I will attempt to address the questions asked to me directly.
Regarding Fizeau’s experiment with the cogwheel, I do not have the original source unfortunately.
“Maxwell’s equations showing that the speed of light propagates with a constant velocity is usually used as the motivation for replacing Galilean relativity with Einstein’s relativity. Where do Maxwell’s equations fit into this picture? Were the scientists motivated by testing his prediction of a constant velocity of light or were they just trying to measure the speed of light as a experimental challenge?”
I think this is where a bit of historical rearrangement comes into it for pedagogical purposes. Many of these experiments took place before Maxwell’s electromagnetic wave equation was derived. The derivation of the speed of light from Maxwell’s equations shows that its speed is related to the magnetic and electric properties of the vacuum, which is interesting, especially so in the 19th century I imagine, but by themselves I don’t see how they imply special relativity unless you already assume that the Lorentz transform is the right way to go between reference frames. To show that the speed is the same in all reference frames you’d have to know that, let’s say, the electric attraction between two charges didn’t depend on how fast they were moving with respect to some fixed frame. We now know that’s true, but that information would have to be input into Maxwell’s derivation somehow, which it normally isn’t.
Regarding the definition of Galilean invariance, I was going with the idea that considering dynamics of ball throwers on a riverboat in the rest frame of the shore by subtracting the speed of the river would also work for people playing laser tag. I guess technically this means that Galilean relativity assumes that the Galilean transformation is the correct way to go between frames, which is an equivalent statement to the ones you pasted.
I am not familiar with Schulenberger’s work.
“But please note carefully what I said. I did NOT say that LIGHT has speed c in only one reference frame. I said that A PHOTON has speed c in only one inertial frame, that of the eventual observer. The two observers in relative motion in Einstein’s derivation of the Lorentz Transform did not / could not observe the same photon – they must observe at least two different photons. Any photon that one sees apparently arrives with velocity c relative one’s own frame and not relative to any other’s frame.”
There is no need to even talk about photons in special relativity, photons are not present. You need to quantise the EM field to have photons and this is one of the most involved processes in quantum field theory. Photons are not small billiard balls. Regardless, the events of emission and detection exist in all frames – they are not coordinate dependent. Any other statement borders on misinformation.
“I don’t think one can detect a photon destined to be observed in some other reference frame. If I am wrong please let me know. But if this is correct, then it removes some of the strange and mysterious aspects of SRT for me. Thanks.”
Photons are not observed “in a frame”. Frames are only different ways of putting different coordinates on the same events in space-time.
“Your pet peeve seems to be wrong. There is nothing special about any particular inertial frame and the speed of light is going to be the same in any inertial frame. In fact, the special relativity “inertial frame” is generally just a substitute for a particular type of coordinate system on Minkowski space. In general, you can use any coordinate system and get the same results. The propagation of light is not tied into any particular coordinate system, it is a property of space-time.”
Thank you for your response. But please note carefully what I said. I did NOT say that LIGHT has speed c in only one reference frame. I said that A PHOTON has speed c in only one inertial frame, that of the eventual observer. The two observers in relative motion in Einstein’s derivation of the Lorentz Transform did not / could not observe the same photon – they must observe at least two different photons. Any photon that one sees apparently arrives with velocity c relative one’s own frame and not relative to any other’s frame. That is right there in his derivation. I think that is also true for all the experimental verifications of SRT. I don’t think one can detect a photon destined to be observed in some other reference frame. If I am wrong please let me know. But if this is correct, then it removes some of the strange and mysterious aspects of SRT for me. Thanks.
“I’m looking at these issues from the Correspondence Principle point of view.”
I understand. In my backburner project, I am also interested in a correspondence. However, I prefer to disentangle (or at least distinguish) the many roles of “c” in relativity: Speed of light (experimental value), speed of Maxwell-type equations, invariant-speed of relativity theories, unit-conversion factor, etc… Then, when one examines a particular limit… possibly interesting features about the structure of physical theories may be better revealed.
It’s along the lines of … If we discover that the photon has a tiny but nonzero rest-mass (so that its speed is not Lorentz invariant), does special relativity fall apart? I would argue “no”.
“I guess my point of view is that we already have something called “light” which we have experimentally measured its speed to be 3e8 m/s (say, in the frame of the source).
We write down a theory [on electricity and magnetism] yielding a set of PDEs, which satisfies some symmetries under (say) Galilean or Lorentz transformations.
If those PDEs have an invariant-propagation-speed that is infinite or finite but not equal to 3e8 m/s,
then why would one associate the finitely-measured-speed of light with that invariant propagation-speed?
That is to say, one would likely look elsewhere to explain “light”…. There would still be the finite “speed of light” at 3e8 m/s (which wouldn’t be invariant under that PDE’s transformations) and an invariant-speed associated with that PDE.
If those PDEs have an invariant-propagation-speed that is finite and equal to 3e8 m/s,
then one would look further to try to associate light with that PDE.”
I’m looking at these issues from the Correspondence Principle point of view.
“But the speed of a photon is not c in all inertial reference frames. In fact, it is c in only one inertial reference frame, and that is the frame of its eventual absorber / detector.”
Your pet peeve seems to be wrong. There is nothing special about any particular inertial frame and the speed of light is going to be the same in any inertial frame. In fact, the special relativity “inertial frame” is generally just a substitute for a particular type of coordinate system on Minkowski space. In general, you can use any coordinate system and get the same results. The propagation of light is not tied into any particular coordinate system, it is a property of space-time.
“klotza submitted a new PF Insights post
[URL=’https://www.physicsforums.com/insights/speed-light-galilean-relativity/’]The Speed of Light and of Galilean Relativity[/URL]
[IMG]https://www.physicsforums.com/insights/wp-content/uploads/2015/12/speedoflight1-80×80.png[/IMG]
[URL=’https://www.physicsforums.com/insights/speed-light-galilean-relativity/’]Continue reading the Original PF Insights Post.[/URL]”
Alex Klotza,
Excellent post, thank you! I’m delighted to know that there is someone out there who is taking an honest look at physics fundamentals.
You’ve probably not heard of John R Schulenberger. This link, [URL]http://www.tandfonline.com/doi/abs/10.1080/03605308008820135[/URL]
might get you to some references to his paper, “Isomorphisms of hyperbolic systems and the aether.” At the level of deeply fundamental physics you may find it interesting, because he shows that the M-M experiment could not have detected the aether.
Thus, while the old “aether” concept has been left by the wayside, because relativistic concepts bypassed it like a Texas driver ignores roadkill, however unusual it might be, the aether has not yet been mathematically discredited.
Schulenberger was not the ordinary physicist. He obtained his first university level degree in Electrical Engineering by merely testing for it, without taking or auditing courses. He remained on the fringes of academia throughout his life, living simply and economically, making conventional income by bicycling to Idaho and building a house every year with a brother. He made beer and cigar money in Tucson by translating Russian math and physics papers for the University of Arizona. His life’s focus was the investigation of fundamental physics concepts. You might find him to be a kindred spirit. Or, you might not.
“Writing down a Galilei-covariant form of the Maxwell’s equations”
Can you be more explicit? I wasn’t aware that there was such a thing. Maxwell’s equations are Maxwell’s equations; they are Lorentz invariant, not Galilean invariant.
“Hmm, quoting is not going right. So let me repeat. Writing down a Galilei-covariant form of the Maxwell’s equations gives eqn.’s similar to Newton’s grav.eqn’s. Hence instanteneous propagation, hence an infinite speed of light.
”
I guess my point of view is that we already have something called “light” which we have experimentally measured its speed to be 3e8 m/s (say, in the frame of the source).
We write down a theory [on electricity and magnetism] yielding a set of PDEs, which satisfies some symmetries under (say) Galilean or Lorentz transformations.
If those PDEs have an invariant-propagation-speed that is infinite or finite but not equal to 3e8 m/s,
then why would one associate the finitely-measured-speed of light with that invariant propagation-speed?
That is to say, one would likely look elsewhere to explain “light”…. There would still be the finite “speed of light” at 3e8 m/s (which wouldn’t be invariant under that PDE’s transformations) and an invariant-speed associated with that PDE.
If those PDEs have an invariant-propagation-speed that is finite and equal to 3e8 m/s,
then one would look further to try to associate light with that PDE.
“By considering these experiments, I think one could discount the idea that light’s speed simply adds to the speed of its source, as is required by Galilean relativity.”
Hi [USER=569939]@klotza[/USER]:
I very much liked your article, but the sentence above confuses me. In the article
[INDENT][URL]https://en.wikipedia.org/wiki/Galilean_invariance[/URL][/INDENT]
Wikipedia says
[INDENT]”Galilean relativity states that the laws of motion are the same in all [URL=’https://en.wikipedia.org/wiki/Inertial_frame’]inertial frames[/URL].”[/INDENT]
Other Internet sources say the same thing in different words. For example
[INDENT][URL]http://physics.ucr.edu/~wudka/Physics7/Notes_www/node47.html[/URL][/INDENT]
says
[INDENT]”Generalizing these observations Galileo postulated his relativity hypothesis: any two observers moving at constant speed and direction with respect to one another will obtain the same results for all mechanical experiments.”[/INDENT]
What confuses me is that these definitions of Galilean relativity do not seem to imply what the quote above from your article says. Were you perhaps thinking of some other Galileo writings in which he said that light’s speed adds to the speed of its source?
Regards,
Buzz
Really nice article. It’s always fun to read about some of the elegant experiments that scientists designed long ago.
Maxwell’s equations showing that the speed of light propagates with a constant velocity is usually used as the motivation for replacing Galilean relativity with Einstein’s relativity. Where do Maxwell’s equations fit into this picture? Were the scientists motivated by testing his prediction of a constant velocity of light or were they just trying to measure the speed of light as a experimental challenge?
Nice write-up. But it repeats my pet peeve that is in all the textbooks. That is some version of: “The velocity of light is c in all inertial reference frames”. It takes a really generous reading of that sentence to have it be correct. Yes, the speed of light is independent of the emitter’s speed. But the speed of a photon is not c in all inertial reference frames. In fact, it is c in only one inertial reference frame, and that is the frame of its eventual absorber / detector. That fact is right there in Einstein’s brilliant derivation of the Lorentz Transform. It just seems to me that it should be explicitly stated.
see this video
[MEDIA=youtube]ScN-btW8ST8[/MEDIA]
near 0:56
Hi
I was reading your article and you mentioned Fizeau’s experiment to measure the speed of light using a cog wheel.
I believe it said that he shone a light some 15 km to a mirror and then it was reflected back.
I have tried to find more details about how he actually achieved this. For example, what did he use as a light source and what did he use the drive the cog wheel? Any ideas?
I have not yet been able to track down any proper diagrams/drawing of the actuall apparatus he used. A French university tried a while back to reproduce the experiment using a modern laser and hi-tech brushless motor and simply were not able to do the experiment.
“klotza submitted a new PF Insights post
[URL=’https://www.physicsforums.com/insights/speed-light-galilean-relativity/’]The Speed of Light and of Galilean Relativity[/URL]
[IMG]https://www.physicsforums.com/insights/wp-content/uploads/2015/12/speedoflight1-80×80.png[/IMG]
[URL=’https://www.physicsforums.com/insights/speed-light-galilean-relativity/’]Continue reading the Original PF Insights Post.[/URL]”
Nice Insight! [USER=569939]@klotza[/USER]
How do you explain the The Fizeau Water Experiment which demonstrates 3 inertial frames being observed having 3 different speeds relative to each other?
I also very much enjoyed Alex’s article.
Hmm, quoting is not going right. So let me repeat. Writing down a Galilei-covariant form of the Maxwell’s equations gives eqn.’s similar to Newton’s grav.eqn.’s. Hence instantaneous propagation, hence an infinite speed of light.@Klotza Nice article by the way, haven’t said that yet!
Your text, “Thanks!” is already correctly spelled. There’s no need for any corrections.
In my opinion, it is best to leave the “speed of light” ‘c’ as 3e8 m/s always. For this causality parameter, call it “maximum signal speed” ‘c_max’ or “invariant speed” ‘c_invariant’. The dimensionless ratio c/c_max can then take the value of 1 for special relativity and 0 for Galilean relativity.