A Principle Explanation of the “Mysteries” of Modern Physics
All undergraduate physics majors are shown how the counterintuitive aspects (“mysteries”) of time dilation and length contraction in special relativity (SR) follow from the light postulate, i.e., that everyone measures the same value for the speed of light c, regardless of their motion relative to the source (see this Insight, for example). And, we can understand the light postulate to follow from the principle of relativity, sometimes referred to as “no preferred reference frame” (NPRF). Simply put, if the speed of light from a source was only equal to ##c=\frac{1}{\sqrt{\epsilon_o \mu_o}}## (per Maxwell’s equations) for one particular velocity relative to the source, that would certainly constitute a preferred reference frame. Borrowing from Einstein [1], NPRF might be stated (see this Insight):
No one’s “sense experiences,” to include measurement outcomes, can provide a privileged perspective on the “real external world.”
While time dilation and length contraction follow “analytically” from the light postulate, there are those who do not consider the light postulate explanatory, since it does not provide “hypothetically constructed” mechanisms to “synthetically” account for time dilation and length contraction [2][3]. That is, the postulates of SR are “empirically discovered” principles offered without corresponding “constructive efforts.” In what follows, Einstein explains the difference between the two [4]:
We can distinguish various kinds of theories in physics. Most of them are constructive. They attempt to build up a picture of the more complex phenomena out of the materials of a relatively simple formal scheme from which they start out. Thus the kinetic theory of gases seeks to reduce mechanical, thermal, and diffusional processes to movements of molecules – i.e., to build them up out of the hypothesis of molecular motion. When we say that we have succeeded in understanding a group of natural processes, we invariably mean that a constructive theory has been found which covers the processes in question.
Along with this most important class of theories there exists a second, which I will call “principle-theories.” These employ the analytic, not the synthetic, method. The elements which form their basis and starting point are not hypothetically constructed but empirically discovered ones, general characteristics of natural processes, principles that give rise to mathematically formulated criteria which the separate processes or the theoretical representations of them have to satisfy. Thus the science of thermodynamics seeks by analytical means to deduce necessary conditions, which separate events have to satisfy, from the universally experienced fact that perpetual motion is impossible.
The advantages of the constructive theory are completeness, adaptability, and clearness, those of the principle theory are logical perfection and security of the foundations. The theory of relativity belongs to the latter class. In order to grasp its nature, one needs first of all to become acquainted with the principles on which it is based.
Here is why Einstein formulated special relativity as a principle theory [5, pp. 51-52]:
By and by I despaired of the possibility of discovering the true laws by means of constructive efforts based on known facts. The longer and the more despairingly I tried, the more I came to the conviction that only the discovery of a universal formal principle could lead us to assured results.
Despite the fact that “there is no mention in relativity of exactly how clocks slow, or why meter sticks shrink” (no “constructive efforts”), the “empirically discovered” principles of SR are so compelling that “physicists always seem so sure about the particular theory of Special Relativity, when so many others have been superseded in the meantime” [6].
As it turns out, we are in a similar position today with quantum mechanics (QM). For example, QM accurately predicts violations of the Clauser-Horne-Shimony-Holt (CHSH) inequality all the way to the Tsirelson bound for Bell state entanglement without providing a corresponding constructive account (see this Insight, for example). This prompted Lee Smolin to write [7, p. 227]:
So, my conclusion is that we need to back off from our models, postpone conjectures about constituents, and begin again by talking about principles.
Other physicists are also calling for a principal account of QM. Chris Fuchs writes [8, p. 285]:
Compare [quantum mechanics] to one of our other great physical theories, special relativity. One could make the statement of it in terms of some very crisp and clear physical principles: The speed of light is constant in all inertial frames, and the laws of physics are the same in all inertial frames. And it struck me that if we couldn’t take the structure of quantum theory and change it from this very overt mathematical speak — something that didn’t look to have much physical content at all, in a way that anyone could identify with some kind of physical principle — if we couldn’t turn that into something like this, then the debate would go on forever and ever. And it seemed like a worthwhile exercise to try to reduce the mathematical structure of quantum mechanics to some crisp physical statements.
That QM accurately predicts the violation of the CHSH inequality to the Tsirelson bound without spelling out any corresponding constructive account prompted Smolin to write [7, p. xvii]:
I hope to convince you that the conceptual problems and raging disagreements that have bedeviled quantum mechanics since its inception are unsolved and unsolvable, for the simple reason that the theory is wrong. It is highly successful, but incomplete.
Of course, this is precisely the complaint leveled by Einstein, Podolsky, and Rosen (EPR) in their famous paper, “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?” [9]. In an equally famous paper (published after Einstein’s death), John Bell showed how any naïve “completion” of QM via hidden variables could conflict with the predictions of QM for two entangled particles (e.g., see this Insight) [10]. As long as the particles couldn’t communicate faster than light and didn’t have access to information about measurement settings until they were actually being measured, the outcomes for entangled particles with hidden variables would have to obey the “Bell inequality” (the CHSH inequality is a variation thereof). There are two-particle entangled states (“Bell states“) in QM that can violate the Bell inequality (and therefore, the CHSH inequality) and these violations are now experimentally well-confirmed. This “mystery” is in large part responsible for “the conceptual problems and raging disagreements that have bedeviled quantum mechanics.”
However, contra Smolin, we recently showed that Bell state entanglement does not render QM “wrong” or “incomplete” by extending NPRF to include the measurement of another fundamental constant of nature, Planck’s constant h [11][12][30]. As Steven Weinberg points out, measuring an electron’s spin via Stern-Gerlach (SG) magnets constitutes the measurement of “a universal constant of nature, Planck’s constant” [13, p. 3] (Figure 1). So if NPRF applies equally here, everyone must measure the same value for Planck’s constant h, regardless of their SG magnet orientations relative to the source, which like the light postulate is an “empirically discovered” fact. By “relative to the source” of a pair of spin-entangled particles, I mean relative “to the vertical in the [symmetry] plane perpendicular to the line of flight of the particles” [14, p. 943] (Figure 2). Thus, different SG magnet orientations relative to the source constitute different “reference frames” in QM just as different velocities relative to the source constitute different “reference frames” in SR.
Just as NPRF and the speed of light c produce the “mysteries” of time dilation and length contraction in SR, we showed that NPRF and Planck’s constant h produce the “mysteries” of Bell state entanglement and the Tsirelson bound for QM. Generally speaking, Bell spin state entanglement results from the conservation of spin angular momentum, and conservation principles and gauge invariance follow from Wheeler’s “boundary of a boundary” principle, ##\partial\partial = 0## [15][16][17] (Figure 3), which with NPRF underwrite all of physics [17][18].
Specifically, when Alice and Bob make their SG spin measurements at the same angle in the plane of symmetry (same reference frame), conservation of spin angular momentum dictates that they obtain the same result (both +1 or both -1) for the spin triplet states (opposite results for the spin singlet state). This suggests (naively) that if Bob makes his SG spin measurement at angle ##\theta## with respect to Alice (different reference frames), then he should obtain ##\cos{(\theta)}## when Alice obtains +1 in accord with the conservation of spin angular momentum (Figure 4). But, Bob can only ever measure ##\pm 1## per NPRF, just like Alice, so the conservation principle is constrained to hold only on average per NPRF (Figures 5 & 6). Thus, Bell state entanglement and the Tsirelson bound are “mysteries” precisely because of “average-only” conservation, which is conservation per NPRF (Figure 7). So we see that the principle of NPRF reveals an underlying coherence between non-relativistic QM and SR (Figure 8) where others have perceived tension.
For example, in his paper “On the Incompatibility of Special Relativity and Quantum Mechanics” Marco Mamone-Capria’s argument is based on “The EPR correlations … as a simple example of quantum mechanical macroscopic effects with spacelike separation from their causes” [19]. He points out that in 1972 Dirac wrote [20, p. 11]:
The only theory which we can formulate at the present is a non-local one, and of course one is not satisfied with such a theory. I think one ought to say that the problem of reconciling quantum theory and relativity is not solved.
And, Bell also voiced concerns about the compatibility of SR and QM based on quantum entanglement [21, p. 172]:
For me then this is the real problem with quantum theory: the apparently essential conflict between any sharp formulation and fundamental relativity. That is to say, we have an apparent incompatibility, at the deepest level, between the two fundamental pillars of contemporary theory.
Of course, we know QM is not Lorentz invariant and so it deviates trivially from SR in that fashion. In order to get QM from Lorentz invariant quantum field theory one needs to make low energy approximations [22, p. 173]. But, the charge of incompatibility based on QM entanglement actually carries serious consequences, because we have experimental evidence confirming the violation of the CHSH inequality per QM entanglement. So, if the violation of the CHSH inequality is in any way inconsistent with SR, then SR is being challenged empirically. By analogy, we know Newtonian mechanics deviates from SR because it is not Lorentz invariant. As a consequence, Newtonian mechanics predicts a very different velocity addition rule, so suppose we found experimentally that velocities do add as predicted by Newtonian mechanics. That would not merely mean that Newtonian mechanics and SR are incompatible, that would mean Newtonian mechanics has been empirically verified while SR has been empirically refuted. So, if one believes the violation of the CHSH inequality is in any way inconsistent with SR, and one believes the experimental evidence is accurate, then one believes SR has been empirically refuted. Clearly that is not the case, so their reconciliation as regards the violation of the CHSH inequality must certainly obtain in some fashion and here we see how the principle of NPRF does the job.
Further, contrary to Smolin and EPR, Bell state entanglement does not mean that QM is “incomplete” or “wrong.” Rather, QM is as complete as possible per the principles of ##\partial\partial = 0## and NPRF.
Given this result, one immediately wonders if general relativity (GR) can be brought into the mix via NPRF and the gravitational constant G. Of course it can and the associated counterintuitve aspect (“mystery”) in GR is the contextuality of mass. We already showed how this might resolve the missing mass problem without having to invoke non-baryonic dark matter [23][24].
Specifically, I am pointing out the well-known result per GR that matter can simultaneously possess different values of mass when it is responsible for different combined spatiotemporal geometries. Here “reference frame” refers to each of the different spatiotemporal geometries associated with one and the same matter source. Tacitly assumed in this result is of course that G has the same value in each reference frame, which is consistent with NPRF as applied to c and h above. This spatiotemporal contextuality of mass is not present in Newtonian gravity where mass is an intrinsic property of matter. For example, when a Schwarzschild vacuum surrounds a spherical matter distribution the “proper mass” ##M_{p}## of the matter, as measured locally in the matter, can be different than the “dynamic mass” ##M## in the Schwarzschild metric responsible for orbital kinematics about the matter [25, p. 126]. This difference is attributed to binding energy and goes as ##dM_p = \left(1-\frac{2GM(r)}{c^2r}\right)^{-1/2} \: dM##. In another example, suppose a Schwarzschild vacuum surrounds a sphere of Friedmann-Lemaitre-Robertson-Walker (FLRW) dust, as used originally to model stellar collapse [15, pp. 851-853]. The dynamic mass ##M## of the surrounding Schwarzschild metric is related to the proper mass ##M_{p}## of the FLRW dust, as joined at FLRW radial coordinate ##\chi_o##, by
\begin{equation}
\frac{M_p}{M} = \frac{3(2\chi_o -\sin(2\chi_o))}{4 \sin ^3(\chi_o)} \label{massratio}
\end{equation}
where
\begin{equation}
ds^2 = -c^2d\tau^2 + a^2(\tau)\left(d\chi^2 + \sin^2\chi d\Omega^2 \right) \label{FLRWmetric}
\end{equation}
is the closed FLRW metric [26]. I should quickly point out that this may prima facie seem to constitute a violation of the equivalence principle, as understood to mean inertial mass equals gravitational mass, since inertial mass can’t be equal to two different values of gravitational mass. But, the equivalence principle says simply that spacetime is locally flat [27, pp. 68-69] and that is certainly not being violated here nor with any solution to Einstein’s equations.
Thus, contrary to what some believe about SR, QM, and GR collectively, these theories are comprehensive (not “incomplete” as claimed in [7] and [9]) and coherent (not “in conflict” as claimed in [19] and [20]). In order to appreciate the beauty of these theories collectively, one need only view them per the principles of ##\partial\partial = 0## and NPRF with their associated “mysteries” corresponding to c, h, and G, respectively. I close with this quote from Wolfgang Pauli [28, p. 33]:
‘Understanding’ nature surely means taking a close look at its connections, being certain of its inner workings. Such knowledge cannot be gained by understanding an isolated phenomenon or a single group of phenomena, even if one discovers some order in them. It comes from the recognition that a wealth of experiential facts are interconnected and can therefore be reduced to a common principle. In that case, certainty rests precisely on this wealth of facts. The danger of making mistakes is the smaller, the richer and more complex the phenomena are, and the simpler is the common principle to which they can all be brought back. … ‘Understanding’ probably means nothing more than having whatever ideas and concepts are needed to recognize that a great many different phenomena are part of a coherent whole.
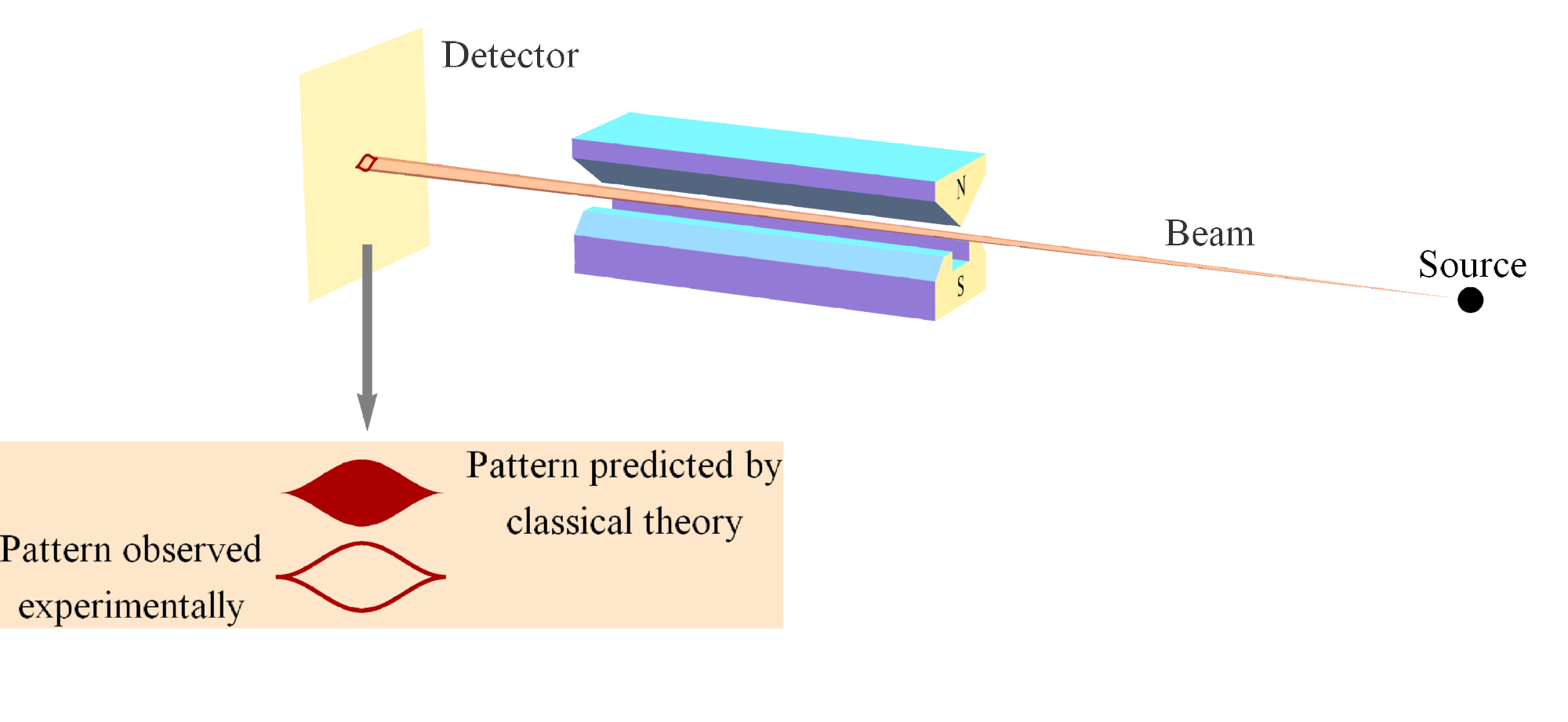
Figure 1. A Stern-Gerlach (SG) spin measurement showing the two possible outcomes, up (##+\frac{\hbar}{2}##) and down (##-\frac{\hbar}{2}##) or +1 and -1, for short. The important point to note here is that the classical analysis predicts all possible deflections, not just the two that are observed. The difference between the classical prediction and the quantum reality uniquely distinguishes the quantum joint distribution from the classical joint distribution for the Bell spin states [29].
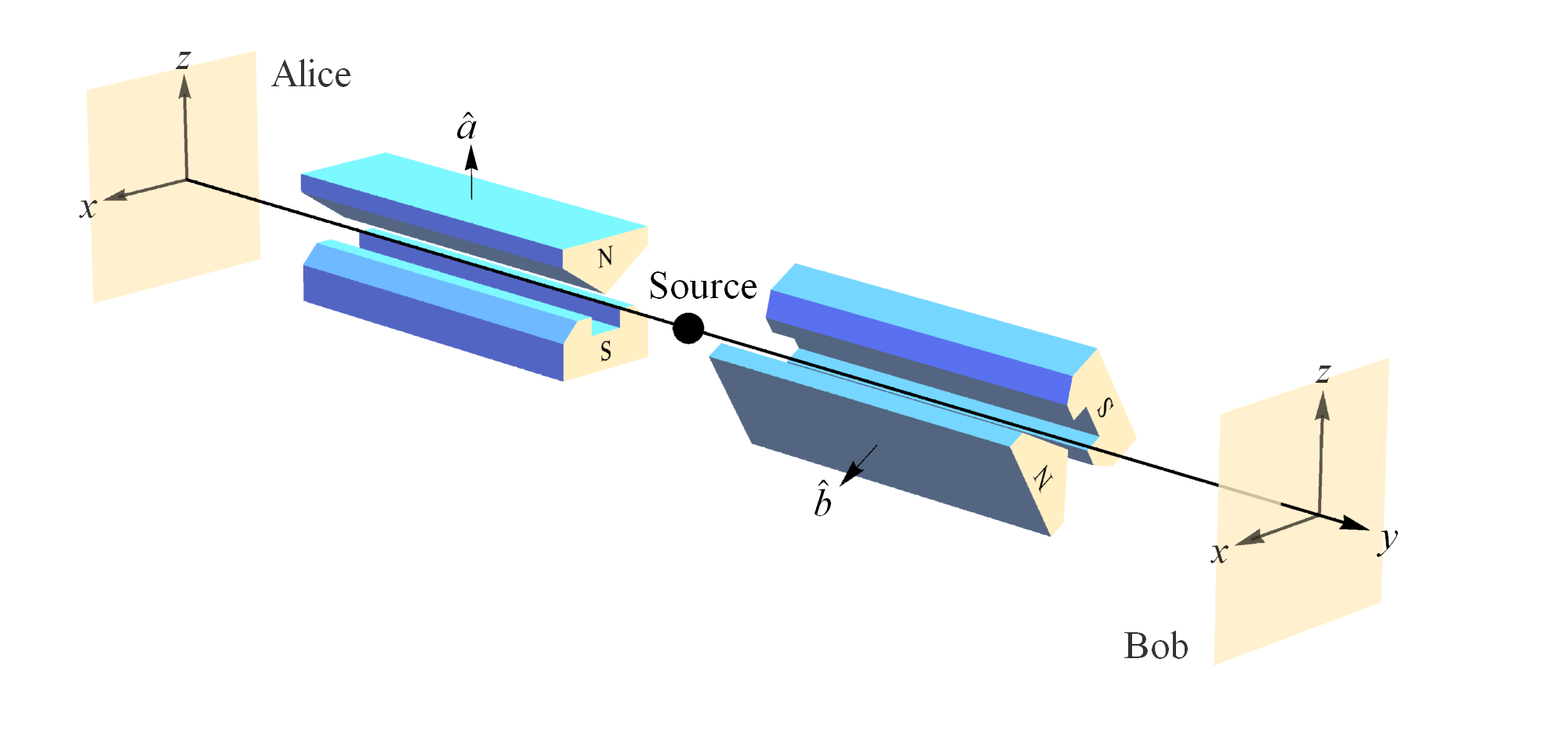
Figure 2. Alice and Bob making spin measurements on a pair of spin-entangled particles with their Stern-Gerlach (SG) magnets and detectors in the xz-plane. Here Alice and Bob’s SG magnets are not aligned so these measurements represent different reference frames.
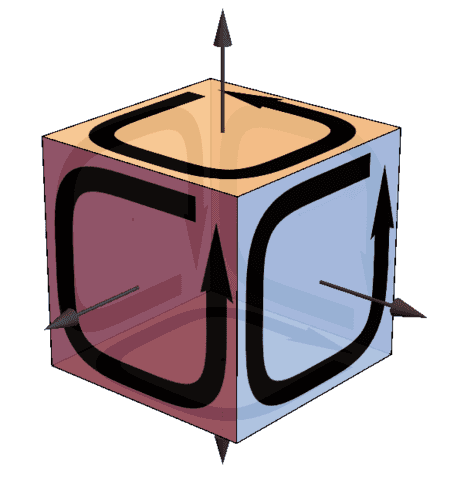
Figure 3. The boundary of a boundary is zero. The oriented plaquettes bound the cube and the directed edges bound the plaquettes. As you can see from the picture, every edge has oppositely oriented directions that cancel out. Thus, the boundaries of the plaguettes (the edges), which bound the cube, sum to zero.
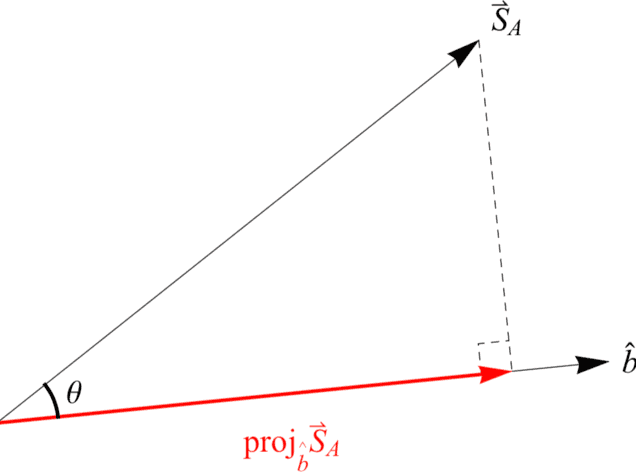
Figure 4. The angular momentum of Bob’s particle ##\vec{S}_B = \vec{S}_A## projected along his measurement direction ##\hat{b}##. This does not happen with spin angular momentum because Bob must always measure ##\pm 1##, no fractions, in accord with NPRF.
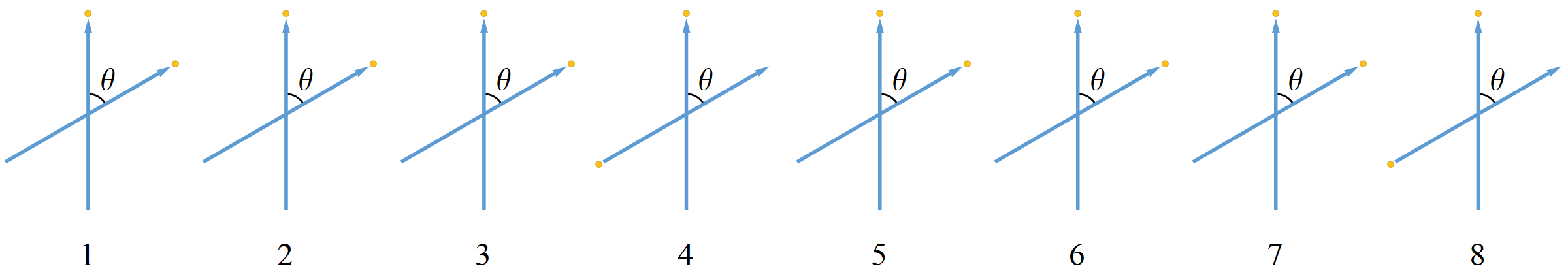
Figure 5. A spatiotemporal ensemble of 8 experimental trials for the spin triplet states showing Bob’s outcomes corresponding to Alice’s +1 outcome when ##\theta = 60^\circ##. Blue arrows depict SG magnet orientations and yellow dots depict the measurement outcomes. Spin angular momentum is not conserved in any given trial, because there are two different measurements being made, i.e., outcomes are in two different reference frames, but it is conserved on average for all 8 trials (six up outcomes and two down outcomes average to ##\cos{(60^\circ)}=\frac{1}{2}##).
Figure 6. Average View for the Spin Triplet States. Reading from left to right, as Bob rotates his SG magnets relative to Alice’s SG magnets for her +1 outcome, the average value of his outcome varies from +1 (totally up, arrow tip) to 0 to -1 (totally down, arrow bottom). This obtains per conservation of spin angular momentum on average in accord with no preferred reference frame. Bob can say exactly the same about Alice’s outcomes as she rotates her SG magnets relative to his SG magnets for his +1 outcome. That is, their outcomes can only satisfy conservation of spin angular momentum on average in different reference frames, because they only measure ##\pm 1##, never a fractional result. Again, just as with the light postulate of special relativity, we see that no preferred reference frame leads to a counterintuitive result. Here it requires quantum outcomes ##\pm 1 \left(\frac{\hbar}{2}\right)## for all measurements leading to the “mystery” of “average-only” conservation.
Figure 7. Bub’s version of Wheeler’s question “Why the quantum?” is “Why the Tsirelson bound?” The “constraint” is the principle of “conservation per no preferred reference frame”.
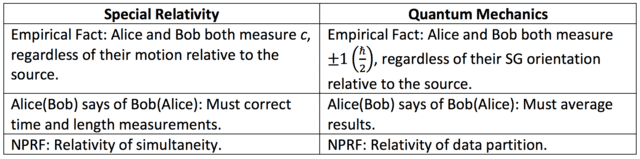
Figure 8. Comparing SR with QM according to no preferred reference frame (NPRF). Because Alice and Bob both measure the same speed of light c, regardless of their motion relative to the source per NPRF, Alice(Bob) may claim that Bob’s(Alice’s) length and time measurements are erroneous and need to be corrected (length contraction and time dilation). Likewise, because Alice and Bob both measure the same values for spin angular momentum ##\pm 1## ##\left(\frac{\hbar}{2}\right)##, regardless of their SG magnet orientation relative to the source per NPRF, Alice(Bob) may claim that Bob’s(Alice’s) individual ##\pm 1## values are erroneous and need to be corrected (averaged, Figures 5 & 6). In both cases, NPRF resolves the “mystery” it creates. In SR, the apparently inconsistent results can be reconciled via the relativity of simultaneity. That is, Alice and Bob each partition spacetime per their own equivalence relations (per their own reference frames), so that equivalence classes are their own surfaces of simultaneity and these partitions are equally valid per NPRF. This is completely analogous to QM, where the apparently inconsistent results per the Bell spin states arising because of NPRF can be reconciled by NPRF via the “relativity of data partition.” That is, Alice and Bob each partition the data per their own equivalence relations (per their own reference frames), so that equivalence classes are their own +1 and -1 data events and these partitions are equally valid.
References
- A. Einstein, Journal of the Franklin Institute 221(3), 349 (1936).
- H. Brown, Physical Relativity: Spacetime Structure from a Dynamical Perspective (OxfordUniversity Press, Oxford, UK, 2005).
- H. Brown, O. Pooley, in The Ontology of Spacetime, ed. by D. Dieks (Elsevier, Amsterdam, 2006), p. 67.
- A. Einstein, London Times pp. 53–54 (1919).
- A. Einstein, in Albert Einstein: Philosopher-Scientist, ed. by P.A. Schilpp (Open Court, La Salle,IL, USA, 1949), pp. 3–94.
- P. Mainwood. What Do Most People Misunderstand About Einstein’s Theory Of Relativity? (2018).
- L. Smolin, Einstein’s Unfinished Revolution: The Search for What Lies Beyond the Quantum (Penguin Press, New York, 2019).
- C. Fuchs, B. Stacey, in Quantum Theory: Informational Foundations and Foils, ed. by G. Chiribella, R. Spekkens (Springer, Dordrecht, 2016), pp. 283–305.
- A. Einstein, B. Podolsky, N. Rosen, Physical Review 47, 777 (1935).
- J. Bell, Physics 1, 195–200 (1964).
- W. Stuckey, M. Silberstein, T. McDevitt, I. Kohler, Entropy 21, 692 (2019). https://arxiv.org/abs/1807.09115
- W. Stuckey, M. Silberstein, T. McDevitt, T. Le, Scientific Reports 10, 15771 (2020). www.nature.com/articles/s41598-020-72817-7
- S. Weinberg. The Trouble with Quantum Mechanics (2017).
- N. Mermin, American Journal of Physics 49(10), 940 (1981).
- C. Misner, K. Thorne, J. Wheeler, Gravitation (W.H. Freeman, San Francisco, 1973).
- D. Wise, Classical and Quantum Gravity 23(17), 5129 (2006).
- A. Kheyfets, J. Wheeler, International Journal of Theoretical Physics 25, 573–580 (1986).
- M. Silberstein, W. Stuckey, Entropy 22, 551 (2020). https://www.mdpi.com/1099-4300/22/5/551/pdf
- M. Mamone-Capria, Journal for Foundations and Applications of Physics 8(2), 163 (2018). https://arxiv.org/pdf/1704.02587.pdf
- P. Dirac, in The Physicist’s Conception of Nature, ed. by J. Mehra (Reidel, Boston, 1973).
- J. Bell, Speakable and Unspeakable in Quantum Mechanics (Cambridge University Press, Cambridge, Massachusetts, 1987).
- A. Zee, Quantum Field Theory in a Nutshell (Princeton University Press, Princeton, 2003).
- W. Stuckey, T. McDevitt, A. Sten, M. Silberstein, International Journal of Modern Physics D 25(12), 1644004 (2016). http://arxiv.org/abs/1605.09229
- W. Stuckey, T. McDevitt, A. Sten, M. Silberstein, International Journal of Modern Physics D 27(14), 1847018 (2018). https://arxiv.org/abs/1509.09288
- R. Wald, General Relativity (University of Chicago Press, Chicago, 1984).
- W. Stuckey, American Journal of Physics 62(9), 788 (1994).
- S. Weinberg, Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity (John Wiley & Sons, New York, 1972).
- W. Heisenberg, Physics and Beyond: Encounters and Conversations (Harper & Row, New York, 1971).
- A. Garg, N. Mermin, Physical Review Letters 49, 901 (1982).
- M. Silberstein, W. Stuckey, T. McDevitt, Entropy 23(1), 114 (2021). https://www.mdpi.com/1099-4300/23/1/114/htm
PhD in general relativity (1987), researching foundations of physics since 1994. Coauthor of “Beyond the Dynamical Universe” (Oxford UP, 2018).
doesn't raise conservation of mass-energy issues the way that GR does
"
Can you elaborate on this?
there is no need for a fundamental constant to quantify dark energy, so his approach actually has one less free parameter than GR with a cosmological constant
"
This struck me when I was reading the article you linked to; I think this is a very nice feature of the model.
There is a complete annotated bibliography here.
"
I'm a little confused by this statement in the article:
"Deur's approach does not reproduce the conclusions of conventional classical General Relativity in the weak gravitational fields and spherically asymmetric systems where it dark matter and dark energy phenomena are observed"
At least as regards the effects I described in post #84 (particularly the first one), I don't see how this is correct. AFAIK it is perfectly true that conventional models of galaxies, the ones in which the discrepancy between mass inferred from luminosity and mass inferred from rotation curves is observed, are Newtonian and do not include any post-Newtonian terms, which means they do not include any effects of nonlinearity in the EFE. Those post-Newtonian terms and nonlinear effects are certainly present in principle, and in this respect Deur simply seems to be arguing that, contrary to the assumption underlying conventional models, those effects are not in fact negligible for galaxies. Since the magnitude of those effects is extremely hard to estimate from first principles (it's not feasible to numerically solve the Einstein-Infeld-Hoffman equations for a system of ##10^{11}## bodies), the arguments underlying the conventional assumption that they are negligible are heuristic, and so proposing a model that challenges those assumptions does not strike me as being inconsistent with GR.
Some of the other effects mentioned (such as the confinement invoked to account for dark energy effects) are not, as I understand it, present at all in classical GR, so the article's remark would apply to those; but the article doesn't seem to be drawing any distinction of this kind, it just seems to be making a blanket statement that none of Deur's claimed effects are present in classical GR, and that seems to me to be too strong.
what do you think about the ScienceX News article I linked earlier?
"
I'm not sure about all aspects of the analogy between SR and QM that is described in the paper.
I agree that all observers in relativity having to measure ##c## for the speed of light, regardless of their state of motion, is analogous to all observers in QM having to measure ##\pm \hbar / 2## for spin, regardless of their choice of measurement direction. And I agree that the latter fact requires that, when analyzing conservation of angular momentum in QM, the best we can possibly do is the "average conservation" that the paper describes.
I'm not sure how length contraction or time dilation correspond to the spin "corrections" that have to be made to verify "average conservation", since length and time aren't conserved quantities and the contracted lengths and dilated times that a given observer assigns to objects in motion relative to him are not "corrections" applied to any calculation of conservation.
I'm wondering, though, if the latter issue could be addressed by looking at energy and momentum instead of time and length, since they are "corrected" by the same factors and they are conserved quantities. That would still leave as a difference between SR and QM the fact that the SR conservation laws are not average only.
I would like to see their fits of X-ray cluster mass profiles, since that's where MOND fails miserably and MOND also works well with galactic rotation curves. I would like to see their fits of the type Ia SN data and the Planck CMB anisotropy data, since they claim to account for dark energy effects.
"
These are good points, I would like to see the same things for Deur's proposed model.
The work is highly speculative of course, since it's based on a direct quantization of GR which we know doesn't work.
"
Actually, from what I can see, the effects described in the 2009 Deur paper I linked to, and the 2020 paper @ohwilleke linked to, are classical effects and should be present in a classical GR model. His investigation was motivated by considering graviton-graviton interactions in a quantum field theory of a spin-2 field, but the actual Lagrangian he presents in the 2009 paper is classical; it's just a power series expansion of the standard Einstein-Hilbert Lagrangian around a zero order flat metric.
It seems to me that there are basically two classical effects he is describing:
(1) Nonlinearity in the Einstein Field Equation, which leads to terms in a post-Newtonian expansion that amount to adding a ##\ln(r)## term to the Newtonian potential, which in turn adds a ##1 / r## term to the Newtonian force, which is basically the same thing that MOND does, but now without requiring any modification to GR;
(2) Non-sphericity, the fact that a galaxy is a flattened disc and not a sphere, which, according to Deur, prevents different nonlinear effects under #1 above from canceling out. If this is correct, it is very interesting, because it would mean that the effects he is talking about would not be visible in a spherically symmetric model of the sort I have been considering in framing the questions I've asked. Which unfortunately makes checking the whole thing a lot harder, since there are no known closed form solutions for the flattened disc case (which is why Deur has to rely on numerical simulations).
You're claiming that the authors, judges, referees, and editors all missed the fact that the application of the effect was backwards.
"
You're misunderstanding my point here. I am not saying that the application of your claimed GR effect in the paper was backwards. I am saying that the only GR effect I can come up with that could apply to ##M_L##, which is where you say the change needs to happen, is in the opposite direction from what it would need to be to resolve the issue your claimed effect is supposed to resolve. That observation in itself doesn't tell me that anything specific in the paper is wrong; it just tells me that, whatever your claimed GR effect is, if it exists, it can't be any of the ones I can come up with. Which is why I keep asking questions to try to help me figure out what your claimed GR effect is, since if it exists it must be something different from any of the ones I have come up with.
All I've seen from you are value judgments and unsupported beliefs
"
No, that's not all you have seen from me. You have also seen specific, simple questions from me. You have not answered my latest one, in post #76. Can you answer it?
"
regarding what is a highly tangential point of the Insight, i.e., principle explanation in modern physics
"
Most of what I have posted in this discussion has not been about that at all. It has been about the GR effect claimed in your paper which I have not been able to understand.
Let me review the scholarly process at work here.
"
I am not trying to criticize or disparage the scholarly process. I am certainly not trying to claim that the journal should not have published your paper. That is entirely up to them. I am also not at all saying that your Insights article should not have been written or that PF should not have published it.
I am just trying to understand the heuristic argument you are making in the paper regarding the presence of a GR effect with the claimed properties. Lecturing me on the scholarly process does not help me with that at all. What would help me with that would be if you would answer the questions I posed in post #76. If you're not going to do that, I'll just bow out of the discussion since I have nothing further either to gain from it or to contribute to it.
You may not respect the authorities and/or your colleagues in the community, but you nonetheless have to get them to sign off on your ideas if you want your ideas distributed and/or recognized by that community. I understand PF only allows Insights based on ideas that have successfully passed this process. My Insight is based 100% on that process. I have not seen you post any references refuting anything in my Insight that have passed that process. All I've seen from you are value judgments and unsupported beliefs regarding what is a highly tangential point of the Insight, i.e., principle explanation in modern physics. For example, what do you think about the ScienceX News article I linked earlier?
If you can cite a no-go theorem having passed the scholarly process, you will save me a lot of time in the future. Otherwise, you're wasting a lot of my time responding to your unsupported beliefs and value judgments. I'm sorry, I just can't spare the time in that direction, Peter.
How does this compare to the works of Deur
"
A more pertinent paper by Deur for this discussion might be this one:
https://arxiv.org/pdf/0901.4005.pdf
This is ref. 3 in the paper linked to in the quote above, and appears to be the original paper presenting his proposed effect and estimating its impact on galaxy rotation curves.
You've totally misunderstood what was published.
"
Btw, I should clarify something: nothing I have said should be taken as claiming that this statement just quoted is wrong. In fact I don't understand the claims being made in the paper about things like "globally determined" vs. "locally determined" mass, or how an observer in the surrounding FLRW dust region in what I quoted in my previous post just now can measure ##M_p##. What I am trying to figure out is whether I don't understand because I've missed something, or because the paper is actually wrong in its claims about the existence of an effect within standard GR that has the necessary properties.
So far, the responses I have gotten have moved me in the direction of "the paper is actually wrong", but that's still just opinion on my part because I still have not gotten a response which helps me to make sense of the parts of the paper that I can't understand. In my previous post I tried to frame a simple question that focuses on one particular part that I can't understand, in the hope that I will get a response that helps me to understand it. I may still not agree with it even after I understand it, but I would much prefer, if I am going to end up disagreeing, to be able to do so with confidence that I understand the claim I am disagreeing with. That is why I have persisted in asking questions.
"
The spacetime geometry of the surrounding FLRW dust will be unaffected by the intervening Schwarzschild vacuum, so observers in the surrounding FLRW dust (global context) will obtain the “globally determined” proper mass ##M_p## for the collapsed dust ball while observers in the Schwarzchild vacuum (local context) will obtain the “locally determined” dynamic mass ##M## for the collapsed dust ball.
"
The question is this: how will each of these observers obtain the masses they are said to obtain in the above?
I'll give what I understand to be the answer for the observer in the Schwarzschild vacuum region: this observer puts a test object into orbit about the "galaxy" (which in this model is actually a collapsing FLRW dust region, but let's ignore that and assume it's a stationary compact region like a galaxy) and measures its orbital parameters, and uses the well-known equations for orbits in Schwarzschild spacetime to derive the mass ##M## of the central object.
So to rephrase the question: first, is my understanding above correct? And if it isn't, what is the correct description of how the observer in the Schwarzschild vacuum region will measure his ##M##?
And second, how will the other observer, the one in the surrounding FLRW dust region, measure ##M_p##? What I am looking for is an explicit description of a measurement procedure similar to what I described above for the Schwarzschild observer. I have speculated about this in previous posts, but since you are saying I have misunderstood the paper, I will refrain from speculating. I would like you (@RUTA) to tell me.
The judges at the Gravity Research Foundation, journal referees, and journal editors disagree with you there, as it received Honorable Mention and was published.
"
I don't accept arguments from authority. In fact, when I see someone retreat into an argument from authority, my Bayesian prior is to raise my estimate of the probability that their claims are mistaken. Just to help you calibrate your estimate of me, I posted a thread in the relativity forum not too long ago proposing that an argument by Schild that is presented in MTW is erroneous. The thread is linked below if you care to read it; there is quite a bit of good discussion by a number of PF members, several of whom raised good points I had not thought of:
https://www.physicsforums.com/threa…me-dilation-imply-spacetime-curvature.919181/
"
You've totally misunderstood what was published.
"
If that's the only response you can give, I'm afraid we have reached an impasse. But I'll try and frame a simpler question that might elicit a more helpful response from you in a follow-up post.
"
You're claiming that the authors, judges, referees, and editors all missed the fact that the application of the effect was backwards. But, it's obvious to you. Doesn't that give you pause at all?
"
No. I have no idea who these people are or what expertise they have in GR.
I won't respond to the rest of your post since I don't see any basis there for a constructive discussion. But, as I said, I'll try to frame a simpler question in a follow-up post.
So it sounds like this is basically a discovery of an empirical formula that works well with broad applicability that is only dimly motivated by very top level concepts in GR, which doesn't mean that it isn't potentially a big deal, or that it might be possible to reverse engineer the formula to determine what kind of gravitational effect is necessary to produce this formula.
How does this compare to the works of Deur who derives a similar effect from the self-interactions of gravitons a naive effort to build a quantum gravity LaGrangian, more or less from first principles and informed by an analogy to parallel QCD equations (although his approach is not inherently quantum in nature and can also be described classically in terms of the self-interactions of a classical gravitational field)?
The formula seems very different but the result seems to be very similar.
"
I'll check that out, thnx.
This is probably where I see the disconnect.
First, as I think I've said before, I don't think "heuristically" is enough. You can't just assume the effect you want to be there actually is there in a solution that is applicable to a galaxy and our observations of it. You have to show that the effect is there and of the right general order of magnitude. Just assuming it's there because it appears to be there in a different solution is not enough.[/quote]
The judges at the Gravity Research Foundation, journal referees, and journal editors disagree with you there, as it received Honorable Mention and was published.
"
Second, the "fact" you are talking about, even in the solution you explicitly examine (collapsing FRW surrounded by Schwarzschild vacuum surrounded by expanding FRW), is not an effect that produces what you are looking for, as you are describing it later in your post. More on that below.
This is simply invalid handwaving. "GR allows for simultaneously differing mass values for one and the same matter" is not a magic wand. It's a specific statement about a specific pair of measurements, and it has a specific effect, and that effect is not what you're looking for.
A correct application of "GR allows for simultaneously differing mass values for one and the same matter" would look like this:
The mass ##M_L##, because it is obtained from observed luminosities, is a sum of "locally measured" masses–masses that would be measured by an observer in the same local region of the galaxy as the stars whose luminosities are being observed. Those are the masses that appear in the mass-luminosity relationships that are being used.
The mass ##M_R##, because it is obtained from observed rotation curves, is a sum of "externally measured" masses–masses that would be measured by an observer in the vacuum region outside the system. (There are some technicalities to this, but I think it's reasonable for the case under consideration.)
GR allows "externally measured" masses to be different from "locally measured" masses for systems like galaxies, because the latter include the effects of gravitational binding energy while the former do not. But that effect, as I've already noted, is in the wrong direction: "locally measured" masses are larger than "externally measured" masses, not smaller. So if the only matter in a galaxy is luminous matter, we would expect a GR correction to make ##M_L > M_R##, which is the opposite of what we need. (Also, the magnitude of this correction is small; it is of rough order of magnitude ##G M / c^2 R##, where ##R## is some appropriate value for the radius of the galaxy. For all galaxies we know of, this correction is a tiny fraction of a percent at best.)
GR also includes spatial curvature, which is not included in the standard Newtonian models of galaxies, but as I've already said, this does not affect either ##M_R## or ##M_L##; it only affects our estimate of average density.[/quote]
You've totally misunderstood what was published. Your analysis is so far off the mark, I would have to reproduce most of the paper to correct it here. Think carefully about your assertion, Peter. You're claiming that the authors, judges, referees, and editors all missed the fact that the application of the effect was backwards. But, it's obvious to you. Doesn't that give you pause at all?
"
There is no other GR effect I know of that is applicable here. [/quote]
Is that your basis for a no-go theorem?
"
As an empirical finding, this is fine. But it does not support any claim that there is a valid GR correction that will produce such a functional form. I don't see how there can be one, for the reasons given above. [/quote]
Unfortunately, the reasons given above are totally misguided.
"
And as I've already remarked, and you have agreed, you are not deriving your functional form from any underlying GR equations; you are just assuming it as an ansatz and seeing how it fits the data. So the fact that it fits the data well does not provide any support for the claim that there is in fact a valid GR correction that leads to your ansatz.[/quote]
That is true.
"
So if your functional form turns out to be valid (i.e., if it doesn't turn out to be just another way of representing the effects of dark matter), I think it will be because it is a reasonable approximation to some underlying effect that is not present in GR, but is present in some modified theory (possibly derived from quantum gravity) that includes effects that are not present in GR. (I personally think this is extremely unlikely, but that's just my opinion; once we actually have a working theory of gravity, possibly quantum gravity, that goes beyond GR, we'll see what it says.)"
Do you have any calculations or references to support your beliefs here? Because the reasons given above are totally erroneous. You have totally misunderstood the paper and I don't have the time to help you there, my friend.
That fact alone is used heuristically
"
This is probably where I see the disconnect.
First, as I think I've said before, I don't think "heuristically" is enough. You can't just assume the effect you want to be there actually is there in a solution that is applicable to a galaxy and our observations of it. You have to show that the effect is there and of the right general order of magnitude. Just assuming it's there because it appears to be there in a different solution is not enough.
Second, the "fact" you are talking about, even in the solution you explicitly examine (collapsing FRW surrounded by Schwarzschild vacuum surrounded by expanding FRW), is not an effect that produces what you are looking for, as you are describing it later in your post. More on that below.
"
The correction we proposed is simply to replace ##M_L## in the Newtonian acceleration with a corrected value, since the mass of the matter responsible for the acceleration is being measured in two different ways and GR allows for simultaneously differing mass values for one and the same matter
"
This is simply invalid handwaving. "GR allows for simultaneously differing mass values for one and the same matter" is not a magic wand. It's a specific statement about a specific pair of measurements, and it has a specific effect, and that effect is not what you're looking for.
A correct application of "GR allows for simultaneously differing mass values for one and the same matter" would look like this:
The mass ##M_L##, because it is obtained from observed luminosities, is a sum of "locally measured" masses–masses that would be measured by an observer in the same local region of the galaxy as the stars whose luminosities are being observed. Those are the masses that appear in the mass-luminosity relationships that are being used.
The mass ##M_R##, because it is obtained from observed rotation curves, is a sum of "externally measured" masses–masses that would be measured by an observer in the vacuum region outside the system. (There are some technicalities to this, but I think it's reasonable for the case under consideration.)
GR allows "externally measured" masses to be different from "locally measured" masses for systems like galaxies, because the latter include the effects of gravitational binding energy while the former do not. But that effect, as I've already noted, is in the wrong direction: "locally measured" masses are larger than "externally measured" masses, not smaller. So if the only matter in a galaxy is luminous matter, we would expect a GR correction to make ##M_L > M_R##, which is the opposite of what we need. (Also, the magnitude of this correction is small; it is of rough order of magnitude ##G M / c^2 R##, where ##R## is some appropriate value for the radius of the galaxy. For all galaxies we know of, this correction is a tiny fraction of a percent at best.)
GR also includes spatial curvature, which is not included in the standard Newtonian models of galaxies, but as I've already said, this does not affect either ##M_R## or ##M_L##; it only affects our estimate of average density.
There is no other GR effect I know of that is applicable here. The only other thing you discuss in the paper that seems at all relevant is the claim on p. 5, after equation (7), that observers in the exterior FRW region will somehow measure ##M_p## instead of ##M##; I have already explained why I don't find that claim to be valid. The only thing I would add to that here is that, as far as I can tell, any such effect, if it were valid, would affect how we infer ##M_R## from observations, not how we infer ##M_L##; but you are saying in what I've quoted above that your claimed effect changes how we infer ##M_L##.
"
We found a functional form for correcting ##M_L## that rivals or beats all competitors across three different astronomical matter distributions — galactic, galactic cluster, and cosmological
"
As an empirical finding, this is fine. But it does not support any claim that there is a valid GR correction that will produce such a functional form. I don't see how there can be one, for the reasons given above. And as I've already remarked, and you have agreed, you are not deriving your functional form from any underlying GR equations; you are just assuming it as an ansatz and seeing how it fits the data. So the fact that it fits the data well does not provide any support for the claim that there is in fact a valid GR correction that leads to your ansatz.
So if your functional form turns out to be valid (i.e., if it doesn't turn out to be just another way of representing the effects of dark matter), I think it will be because it is a reasonable approximation to some underlying effect that is not present in GR, but is present in some modified theory (possibly derived from quantum gravity) that includes effects that are not present in GR. (I personally think this is extremely unlikely, but that's just my opinion; once we actually have a working theory of gravity, possibly quantum gravity, that goes beyond GR, we'll see what it says.)
When you adjoin the FRW and Schwarzschild solutions, the comparative mass can be equal, larger, or smaller, and the matter can be surrounded by vacuum or vice-versa, as I explain in the corresponding AJP paper. That fact alone is used heuristically as follows.
##M_R## is inferred from orbital speeds (or other data in the cases of mass profiles of X-ray clusters and anisotropies in the angular power spectrum of the cosmic microwave background) by assuming Newtonian gravity supplies the centripetal acceleration for UCM of the orbiting stars and gas. When the orbital speeds are measured (via redshifts) we find ##M_R## is much larger than ##M_L##. So, we are considering a correction to Newtonian gravity for a situation that otherwise doesn't seem to warrant it (very small spatial curvature). The correction we proposed is simply to replace ##M_L## in the Newtonian acceleration with a corrected value, since the mass of the matter responsible for the acceleration is being measured in two different ways and GR allows for simultaneously differing mass values for one and the same matter. We found a functional form for correcting ##M_L## that rivals or beats all competitors across three different astronomical matter distributions — galactic, galactic cluster, and cosmological. That is interesting because no other approach works as well across all three distributions. The rivals we compared are:
1. Two different DM distribution models (Burkett and NFW). The functional forms for these DM distributions are not based on any knowledge of the physics for these hypothetical and unlikely (as shown by Carroll) particles.
2. Correction to Newtonian physics (MOND). The ad hoc change of Newtonian acceleration at large scales. There is a relativistic counterpart for this now, but it's ugly and does not satisfy local conservation (not divergence-free).
3. Two different corrections to GR (MSTG and STVG). These are also otherwise unmotivated and do not satisfy local conservation.
Again, none of the rivals match our fits using our simple functional form for the correction of ##M_L## across all three matter distributions. Keep in mind that we're not talking about a new phenomenon here. The missing mass phenomenon was introduced in the 1930's (e.g., Zwicky, F: On the masses of nebulae and clusters of nebulae. The Astrophysical Journal 86, 217-246 (1937)). So, after 80+ years these are still our best guesses.
Conclusion, maybe it's reasonable to consider the idea from GR that matter can simultaneously possess different values of mass based on spatially different measurement contexts. We already know it's true for different temporal contexts, e.g., free neutron mass greater than bound neutron mass. So, is this such a stretch?
That's the best I can do, Peter. Hope it suffices.
Including non-Newtonian effects of the kind implied by "two different measurements of mass for one and the same matter" (which means correcting for things like spatial curvature) should not change either ##M_L## or ##M_R##.
"
On further thought, this way of putting it, while it is correct, might not really get at the issue I'm trying to describe. So let me try it another way.
Suppose we know ##M_R## for some galaxy but we don't know ##M_L## (say we can't see the galaxy directly because it's obscured by a dust cloud, but we've been sent rotation curve data for the galaxy by some alien civilization that isn't behind the dust cloud). What value for ##M_L## would we predict from our knowledge of ##M_R##? Or, to put it another way that makes the logic clearer, what value for total luminosity for the galaxy would we predict from our knowledge of ##M_R##, if we assume that all the matter in the galaxy is luminous (stars) and has similar properties to stars in our own galaxy?
The Newtonian prediction is simple: we expect ##M_L = M_R##, so we just apply some expected distribution of stellar luminosities, plug those into an integral for total luminosity, and use known mass-luminosity relationships to apply the appropriate weighting factors in the integral so that the total mass, given our assumed distribution of stellar luminosities (which we can translate into an assumed distribution of stellar masses) comes out to ##M_L##. This kind of calculation, since it gives an answer for total luminosity that is significantly larger than the total luminosity we actually observe, is the basic argument used by proponents of dark matter: there must be non-luminous matter present to make up the total mass that is needed to account for the observed rotation curves.
Since in actual fact we observe ##M_L < M_R## by some significant factor, if we want to avoid dark matter (and if we also want to avoid modifying our theory of gravity, which is what the paper under discussion wants to do–it wants to find a solution within GR), we need to find some non-Newtonian effect that would modify the above prediction procedure. The first obvious non-Newtonian effect to consider is gravitational binding energy: in Newtonian gravity, binding energy doesn't affect mass, but in GR, it does. However, this effect is in the wrong direction: it leads us to expect ##M_L > M_R## in the above prediction procedure (i.e., it leads us to expect a larger total luminosity than what we would infer by assuming ##M_L = M_R## in the above procedure), because gravitational binding energy is negative; the mass measured "from the outside" by something like rotation curves is smaller than the mass measured "from the inside", by an observer locally that is next to some particular star, and that locally measured mass is what is correlated with the luminosity in our known mass-luminosity relationships. This kind of effect is what I was thinking of in post #65, but I incorrectly mixed it up with space curvature.
A second non-Newtonian effect to consider is space curvature; but as I noted in my previous post (quoted above), that doesn't affect either ##M_R## or ##M_L## in the above prediction procedure (i.e., it doesn't affect the total luminosity we would infer from rotation curve data). It just affects the proper volume we assign to the galaxy, which means it affects the average density we expect a local observer, inside the galaxy, to measure.
So neither of those non-Newtonian effects can account for our observation that ##M_L < M_R##. And I am not aware of any other non-Newtonian effect that would be significant in this scenario, nor does the paper appear to me to suggest one; it only suggests one of the above two, neither of which work.
The only sense I can make of "two different measurements of mass for one and the same matter" gives an answer that makes the discrepancy worse, not better, for the reason I gave in post #65 (it doesn't change ##M_L## and it makes ##M_R## larger, not smaller).
"
Actually, on thinking this over some more, I think I have misstated this a bit. Including non-Newtonian effects of the kind implied by "two different measurements of mass for one and the same matter" (which means correcting for things like spatial curvature) should not change either ##M_L## or ##M_R##. What it should change is our calculation of how much proper spatial volume the mass occupies, i.e., it should change our estimate of the average density (more precisely, proper density, the density measured by an observer locally inside the galaxy) of the matter in a galaxy, as compared to a Newtonian calculation (our estimate of average proper density should be reduced–more spatial volume for the same mass). But it should not change the mass we infer from rotation curves or luminosity at all, because those estimates are independent of our estimate of the average density.
There is no error
"
What I am calling the "error" there is the discrepancy between ##M_R## and ##M_L## when using standard methods to estimate both. So there is an error. I am trying to understand how your proposed method resolves it. See below.
"
they are two different measurements of mass for one and the same matter, as allowed per GR. You can map them one to the other as I showed in the paper.
"
This doesn't answer my question, because I can't make what you're describing here give an answer that resolves the discrepancy. I don't understand how to relate what you are saying in the paper to what I am calling ##M_R## and ##M_L##, or how what you are describing in the paper corrects the discrepancy between the two. The only sense I can make of "two different measurements of mass for one and the same matter" gives an answer that makes the discrepancy worse, not better, for the reason I gave in post #65 (it doesn't change ##M_L## and it makes ##M_R## larger, not smaller). So I'm confused. I am hoping that if you give explicit answers to the two questions I gave, it will help to resolve, or at least reduce, my confusion.
I don't think it's a formal inconsistency; I think it's a physical error.
I don't see how that helps any, but perhaps I'm misunderstanding your argument. Let me try to frame a question that might help to elucidate what your argument is.
We on Earth observe some distant galaxy, and we see a discrepancy between two methods of estimating that galaxy's mass:
Method #1: Measure the rotation curves and use that to estimate the mass from the appropriate dynamical equations. This gives us a mass which I'll call ##M_R##.
Method #2: Measure the aggregate luminosity and use that to estimate the mass using the appropriate relationships between mass and luminosity for stars. This gives us a mass which I'll call ##M_L##.
The discrepancy is that we find ##M_R > M_L## by some significant factor.
Now the question, in two parts:
(1) Which of the two observations above, ##M_R## or ##M_L##, do you think is affected by whatever source of error your paper is describing, and which your alternative method of analysis in the paper claims to fix?
(2) How does your alternative method of analysis fix the error? That is: if your answer to #1 is that ##M_R## as estimated by standard methods is larger than it should be, how does your method make ##M_R## smaller so it matches ##M_L##? Or, if your answer to #1 is that ##M_L## as estimated by standard methods is smaller than it should be, how does your method make ##M_L## larger so it matches ##M_R##?
"
There is no error, they are two different measurements of mass for one and the same matter, as allowed per GR. You can map them one to the other as I showed in the paper.
my read on the paper (and RUTA can correct me if I'm wrong) is that B1 and B2 are the answers here as well, although not so much "the wrong dynamical equations" as the wrong operationalization of the right dynamical equations
"
This was my initial read as well, based on the usage of the terms "proper mass" and "dynamical mass" — basically, that the non-Newtonian effects mean that the "proper mass", which includes corrections for things like spatial curvature, is a better thing to plug into the dynamical equations than the "dynamical mass", which does not include those corrections. However, that can't be the right answer because, as I noted in an earlier post, the correction is in the wrong direction: the corrections due to things like including spatial curvature make the estimate for ##M_R## larger, not smaller.
Now the question, in two parts:
(1) Which of the two observations above, ##M_R## or ##M_L##, do you think is affected by whatever source of error your paper is describing, and which your alternative method of analysis in the paper claims to fix?
(2) How does your alternative method of analysis fix the error? That is: if your answer to #1 is that ##M_R## as estimated by standard methods is larger than it should be, how does your method make ##M_R## smaller so it matches ? Or, if your answer to #1 is that ##M_L## as estimated by standard methods is smaller than it should be, how does your method make ##M_L## larger so it matches ?
"
Perhaps it will also help if I give what I take to be the answers to these questions that would be given by a proponent of (A) dark matter, and (B) MOND.
(A1) ##M_R## is correct, but ##M_L## is too small because it only counts luminous matter.
(A2) There is other matter present, dark matter, which is not luminous and so can't be counted that way. When we add in the mass of dark matter, we get ##M_L + M_D = M_R##, which fixes the discrepancy.
(B1) ##M_L## is correct, but ##M_R## is too large because it is estimated using the wrong dynamical equations.
(B2) MOND changes the dynamical equations so that ##M_R## is smaller and matches ##M_L##, which fixes the discrepancy.
there is a formal inconsistency exactly as you point out
"
I don't think it's a formal inconsistency; I think it's a physical error.
"
The reason for that is we have discrete objects (stars) separated by light years modeled by a continuum
"
I don't see how that helps any, but perhaps I'm misunderstanding your argument. Let me try to frame a question that might help to elucidate what your argument is.
We on Earth observe some distant galaxy, and we see a discrepancy between two methods of estimating that galaxy's mass:
Method #1: Measure the rotation curves and use that to estimate the mass from the appropriate dynamical equations. This gives us a mass which I'll call ##M_R##.
Method #2: Measure the aggregate luminosity and use that to estimate the mass using the appropriate relationships between mass and luminosity for stars. This gives us a mass which I'll call ##M_L##.
The discrepancy is that we find ##M_R > M_L## by some significant factor.
Now the question, in two parts:
(1) Which of the two observations above, ##M_R## or ##M_L##, do you think is affected by whatever source of error your paper is describing, and which your alternative method of analysis in the paper claims to fix?
(2) How does your alternative method of analysis fix the error? That is: if your answer to #1 is that ##M_R## as estimated by standard methods is larger than it should be, how does your method make ##M_R## smaller so it matches ##M_L##? Or, if your answer to #1 is that ##M_L## as estimated by standard methods is smaller than it should be, how does your method make ##M_L## larger so it matches ##M_R##?
Yes, I see that part, but I don't think it's correct. On p. 2, the relationship between proper mass and dynamic mass is given by:
$$
dM_p = \left( 1 – \frac{2 G M}{c^2 r} \right)^{- 1/2} dM
$$
where ##M_p## is proper mass and ##M## is dynamic mass. This formula clearly says that proper mass is locally measured and dynamic mass is externally measured, and the text accompanying the formula agrees with that.
However, on p. 5, in the text you refer to, "proper mass" ##M_p## is now claimed to be "globally determined" and to be the mass that would be measured by an observer in the surrounding FRW region. That is inconsistent with the formula and text on p.2, and also with the standard GR treatment of the spacetime geometry the paper is describing.
In the text on p. 5, you are describing a collapsing FRW region, which I'll call the "interior region" (which, to properly model something like a galaxy, should really be a stationary region containing matter, as I have commented before, but making that change would not affect what I am about to say), surrounded by a Schwarzschild vacuum region, surrounded by an expanding FRW region, which I'll call the "exterior universe". The interior region and Schwarzschild vacuum region together I will call the "bubble".
In the Schwarzschild vacuum region, the mass of the interior region, as measured by orbital dynamics of objects in the Schwarzschild vacuum region, is ##M##. The text on p. 5 agrees with that.
However, the mass of the interior region as measured by an observer in the exterior universe, will not be ##M_p##. An observer in the exterior universe cannot even measure the mass of the interior region directly, using orbital dynamics, because any such orbit will be affected by the stress-energy in the exterior universe that is closer to the bubble than the orbit itself. And if we imagine correcting such a measurement to subtract out the mass in the exterior universe that is affecting the orbit, the remainder will be ##M##, not ##M_p##.
The simplest way to see this is to observe that the function ##m(r)##, which gives the "mass inside radius ##r##" ("mass" meaning the mass measured by orbital dynamics) as a function of the areal radius ##r## centered on the bubble, must be continuous, and its value in the Schwarzschild vacuum region is ##M##. Call the areal radius of the exterior boundary of the bubble ##R_0##. Then we have ##m(R_0) = M##. Now consider ##m(R_0 + dr)##, the value of ##m(r)## just a little way into the exterior universe. This value, by continuity, must be ##M + dM## for ##dM## infinitesimal. But the paper's claim would require it to be ##M_p + dM##, where ##M_p – M## is not infinitesimal. So the paper's claim is inconsistent with continuity of ##m(r)##.
"
Yes, there is a formal inconsistency exactly as you point out. The reason for that is we have discrete objects (stars) separated by light years modeled by a continuum for data collection and curve fitting. I'm thinking of the discrete objects for the use of varying boundaries for varying mass values while modeling the effect in continuum fashion for comparison with the data (which has to be collected that way obviously).
On another note, the mass we obtain from atomic/molecular spectra (ultimately responsible for the mass-luminosity relationship and mass of orbiting gas) is the "locally measured interior mass," since the spectra depend on the mass of the atoms/molecules as would be obtained in a lab on Earth.
One more note and I have to run. Note that the missing mass seems large (as large as a factor of 10 increase), but in terms of spatial curvature on galactic scales, it's tiny. It's in the paper, but I think the spatial curvature for galactic mass densities is on the order of ##10^{-45}m^{-2}##. So, a change by a factor of 10 one way or another isn't very big in terms of GR.
So this T bound says there is some cutoff that makes the classical world have zero QM (neutral monistic) magic (no long-distance-large-object/ensemble-non-local …ness), is that roughly right?
Is it related to “decoherence” which I sort of interpret as the Gaussian noise canceling effect of Lots of long distance large object/ensemble non-localness – which seems plausible but statistical and therefore unsatisfying (FYI that was a joke)… or is it somehow a clean unavoidable deduction?
And if it seemingly analytic and clean could that be due to the fact all Alice and Bob cases are toys (I.e they pretend there are these bounds on the lab to begin with)? Alternatively could it be that there are something more like Tsirelson “gaps” or troughs (waves) recurrence etc?
I know that’s a lot of question, so, just say I’m looking forward to learning about that one. Also, to me it bears on the discussion you and Peter were having about observes “inside the mass” vs “orbiting the mass”
"
The Tsirelson bound is the most QM can violate the Bell inequality known as the CHSH inequality. Classical physics says the CHSH quantity must reside between ##\pm 2##, but the Bell states give ##\pm 2 \sqrt{2}## (the Tsirelson bound). Superquantum correlations respect no-superluminal-signaling and give a CHSH quantity of 4. So, quantum information theorists want to know "Why the Tsirelson bound?" That is, why doesn't Nature produce superquantum correlations? Our answer is "conservation per NPRF." Of classical, QM, and superquantum, only QM satisfies this constraint.
Yes, I see that part, but I don't think it's correct. On p. 2, the relationship between proper mass and dynamic mass is given by:
$$
dM_p = \left( 1 – \frac{2 G M}{c^2 r} \right)^{- 1/2} dM
$$
where ##M_p## is proper mass and ##M## is dynamic mass. This formula clearly says that proper mass is locally measured and dynamic mass is externally measured, and the text accompanying the formula agrees with that.
However, on p. 5, in the text you refer to, "proper mass" ##M_p## is now claimed to be "globally determined" and to be the mass that would be measured by an observer in the surrounding FRW region. That is inconsistent with the formula and text on p.2, and also with the standard GR treatment of the spacetime geometry the paper is describing.
In the text on p. 5, you are describing a collapsing FRW region, which I'll call the "interior region" (which, to properly model something like a galaxy, should really be a stationary region containing matter, as I have commented before, but making that change would not affect what I am about to say), surrounded by a Schwarzschild vacuum region, surrounded by an expanding FRW region, which I'll call the "exterior universe". The interior region and Schwarzschild vacuum region together I will call the "bubble".
In the Schwarzschild vacuum region, the mass of the interior region, as measured by orbital dynamics of objects in the Schwarzschild vacuum region, is ##M##. The text on p. 5 agrees with that.
However, the mass of the interior region as measured by an observer in the exterior universe, will not be ##M_p##. An observer in the exterior universe cannot even measure the mass of the interior region directly, using orbital dynamics, because any such orbit will be affected by the stress-energy in the exterior universe that is closer to the bubble than the orbit itself. And if we imagine correcting such a measurement to subtract out the mass in the exterior universe that is affecting the orbit, the remainder will be ##M##, not ##M_p##.
The simplest way to see this is to observe that the function ##m(r)##, which gives the "mass inside radius ##r##" ("mass" meaning the mass measured by orbital dynamics) as a function of the areal radius ##r## centered on the bubble, must be continuous, and its value in the Schwarzschild vacuum region is ##M##. Call the areal radius of the exterior boundary of the bubble ##R_0##. Then we have ##m(R_0) = M##. Now consider ##m(R_0 + dr)##, the value of ##m(r)## just a little way into the exterior universe. This value, by continuity, must be ##M + dM## for ##dM## infinitesimal. But the paper's claim would require it to be ##M_p + dM##, where ##M_p – M## is not infinitesimal. So the paper's claim is inconsistent with continuity of ##m(r)##.
"
Sorry for the delay, I'm working on another paper now, let me get back to you with my thinking on this :-)
the terms are flipped. See on p. 5
"
Yes, I see that part, but I don't think it's correct. On p. 2, the relationship between proper mass and dynamic mass is given by:
$$
dM_p = \left( 1 – \frac{2 G M}{c^2 r} \right)^{- 1/2} dM
$$
where ##M_p## is proper mass and ##M## is dynamic mass. This formula clearly says that proper mass is locally measured and dynamic mass is externally measured, and the text accompanying the formula agrees with that.
However, on p. 5, in the text you refer to, "proper mass" ##M_p## is now claimed to be "globally determined" and to be the mass that would be measured by an observer in the surrounding FRW region. That is inconsistent with the formula and text on p.2, and also with the standard GR treatment of the spacetime geometry the paper is describing.
In the text on p. 5, you are describing a collapsing FRW region, which I'll call the "interior region" (which, to properly model something like a galaxy, should really be a stationary region containing matter, as I have commented before, but making that change would not affect what I am about to say), surrounded by a Schwarzschild vacuum region, surrounded by an expanding FRW region, which I'll call the "exterior universe". The interior region and Schwarzschild vacuum region together I will call the "bubble".
In the Schwarzschild vacuum region, the mass of the interior region, as measured by orbital dynamics of objects in the Schwarzschild vacuum region, is ##M##. The text on p. 5 agrees with that.
However, the mass of the interior region as measured by an observer in the exterior universe, will not be ##M_p##. An observer in the exterior universe cannot even measure the mass of the interior region directly, using orbital dynamics, because any such orbit will be affected by the stress-energy in the exterior universe that is closer to the bubble than the orbit itself. And if we imagine correcting such a measurement to subtract out the mass in the exterior universe that is affecting the orbit, the remainder will be ##M##, not ##M_p##.
The simplest way to see this is to observe that the function ##m(r)##, which gives the "mass inside radius ##r##" ("mass" meaning the mass measured by orbital dynamics) as a function of the areal radius ##r## centered on the bubble, must be continuous, and its value in the Schwarzschild vacuum region is ##M##. Call the areal radius of the exterior boundary of the bubble ##R_0##. Then we have ##m(R_0) = M##. Now consider ##m(R_0 + dr)##, the value of ##m(r)## just a little way into the exterior universe. This value, by continuity, must be ##M + dM## for ##dM## infinitesimal. But the paper's claim would require it to be ##M_p + dM##, where ##M_p – M## is not infinitesimal. So the paper's claim is inconsistent with continuity of ##m(r)##.
I understand what the actual data says. But the statement of yours that I quoted in post #51 does not seem correct as a description of the effect that is present in the model. In the model, "dynamic mass" is smaller than "proper mass", not larger. So if the "dynamic mass" in the model is supposed to correspond to the orbital mass obtained from rotation curve data, and the "proper mass" in the model is supposed to correspond to the mass obtained from luminosity data, then the model is obviously wrong, since the model says "dynamic mass" should be smaller than "proper mass" but the actual data says "dynamic mass" is larger than "proper mass".
So either the model is wrong or I've misunderstood how the "dynamic mass" and "proper mass" in the model are supposed to correspond to the "orbital mass" (from rotation curves) and the "proper mass" (from luminosity) in the data.
"
I went back and looked at the paper and you're right, we flipped the terms there from what I said above. I was using the term "dynamical mass" as in astronomy where it corresponds to "orbital mass" (the larger mass). In the paper, the term "dynamical mass" corresponds to what we were going to take as the mass obtained from the mass-luminosity relationship, i.e., the "local" value, since that's how one ultimately obtains the ML relationship. Thus, the terms are flipped. See on p. 5 starting with "Suppose that the Schwarzschild vacuum surrounding the FLRW dust ball in our example above is itself surrounded … ."
The orbital mass obtained from galactic rotation curve data is larger than the locally-determined proper mass (obtained from mass-luminosity ratios for example).
"
I understand what the actual data says. But the statement of yours that I quoted in post #51 does not seem correct as a description of the effect that is present in the model. In the model, "dynamic mass" is smaller than "proper mass", not larger. So if the "dynamic mass" in the model is supposed to correspond to the orbital mass obtained from rotation curve data, and the "proper mass" in the model is supposed to correspond to the mass obtained from luminosity data, then the model is obviously wrong, since the model says "dynamic mass" should be smaller than "proper mass" but the actual data says "dynamic mass" is larger than "proper mass".
So either the model is wrong or I've misunderstood how the "dynamic mass" and "proper mass" in the model are supposed to correspond to the "orbital mass" (from rotation curves) and the "proper mass" (from luminosity) in the data.
Isn't the difference the opposite? The "orbital mass" is what you are calling "dynamic mass" in the paper, and it is smaller than the "proper mass".
"
The orbital mass obtained from galactic rotation curve data is larger than the locally-determined proper mass (obtained from mass-luminosity ratios for example). That's the "missing mass" problem.
I'm not taking about the effect of geometry on the light rays.
"
Ok, good. I didn't think so, but thanks for confirming.
we know such adjoined solutions allow for larger orbital mass than proper mass
"
Isn't the difference the opposite? The "orbital mass" is what you are calling "dynamic mass" in the paper, and it is smaller than the "proper mass".
The way the momentum-energy content of the matter-occupied region of spacetime affects the geometry of the vacuum region surrounding it is via the coupling between regions as expressed in the extrinsic curvature K on the spatial hypersurface boundary.
"
This is one way of viewing the connection, but not the only one. A drawback of viewing it this way is that the extrinsic curvature you describe depends on how you slice up the spacetime into spacelike slices. In the simple examples you discuss, there is a "preferred" slicing given, roughly speaking, by the "rest frame" of the central body in the asymptotically flat vacuum region. But there won't always be any way to pick out a slicing from any symmetries in the problem.
Also, if we're talking about something like galaxy rotation curves, what we're really interested in is how the stress-energy in the interior region affects the geometry in the interior region. The rotation curves we measure for galaxies are not measurements of objects outside the galaxy orbiting it; they are measurements of objects inside the galaxy, responding to the local spacetime geometry in the galaxy's interior. The geometry in the exterior vacuum region only comes into play to the extent it affects the trajectories of the light rays we see coming from the galaxy, and that effect is going to be small, and is not the kind of effect you're looking for in any case.
"
I don't have hydrodynamic support and I don't want radially expanding or collapsing shells.
"
Yes, that's indeed a problem, but it's a problem in the interior region; you need a stationary blob of matter that is not supported by hydrostatic equilibrium. That doesn't necessarily require the exterior region to be Kerr; in principle the total angular momentum of the whole blob could be zero, with various individual pieces of matter in the blob orbiting in different planes so their individual orbital angular momenta end up cancelling. (Or, more realistically, the total overall angular momentum could be very small compared to other parameters, so it could be ignored or approximated by small corrections to the zero total angular momentum case.) But in the interior, of course, each individual piece of matter has to be in a geodesic orbit about the overall center of mass, since there's no other way for the system to be stationary.
I wasn't referring to any potential paper I am working on; I'm not an academic. If I find the time to make any calculations along the lines I was describing, I will post them here.
"
If you do find something that's not suitable for PF (since it's not been properly refereed), please notify me! Let me say specifically what I hope someday to have the time to explore.
The way the momentum-energy content of the matter-occupied region of spacetime affects the geometry of the vacuum region surrounding it is via the coupling between regions as expressed in the extrinsic curvature K on the spatial hypersurface boundary. The goal would be to find the cumulative functional form for nested embeddings, i.e., K1 to K2 to … . How does the mass M in a vacuum geometry vary from "shell" to "shell" as a function of the K's? You can see why I was considering a Kerr solution, since I don't have hydrodynamic support and I don't want radially expanding or collapsing shells.
https://www.physicsforums.com/threads/is-there-a-simple-dark-matter-solution-rooted-in-gr.994526/
I ask because it seems to me that one of the papers (ref. 24, the one we have been discussing here) is using standard GR, while the other (ref. 23) is not–it is proposing a model in which the GR assumption of spacetime as a continuous manifold is only an approximation. If I am correct about that, discussion of those two papers should be in separate threads; the thread I linked to above, which is in the Beyond the Standard Model forum, would be appropriate for ref. 23, since it is proposing a model that goes beyond standard GR, but discussion of ref. 24, if it were to go anywhere other than this thread, should properly be in the relativity forum, since that paper is using standard GR.
if you'd like another pair of eyes on your paper before submitting it, send me the arXiv link when you get it done
"
I wasn't referring to any potential paper I am working on; I'm not an academic. If I find the time to make any calculations along the lines I was describing, I will post them here.
there is a tacit assumption of the DM models that is just as speculative because they have no candidates for what they're placing in the stress-energy tensor
"
Yes, that's true. DM models have to assume that there is some non-baryonic kind of matter that will give rise to the stress-energy tensor they need, even though we have not found any such kind of matter in any experiments.
The place I would look first would be interior solutions for the rotating Kerr solution exterior.
"
I'm actually starting with something simpler, a Schwarzschild exterior around a spherically symmetric matter distribution. To add angular momentum to the system, which is the primary reason for using a Kerr exterior, it might be sufficient to just add small correction terms to the interior and exterior metric, rather than trying to use the full-blown Kerr exterior metric, which, as you note, is significantly more complicated. That is how, for example, an experiment like Gravity Probe B is analyzed, as I understand it.
However, I'm not actually convinced that it is necessary to add angular momentum to the system, because the effects that doing that would be required to account for, such as the Lense-Thirring precession that Gravity Probe B was testing, are much too small to be what you are looking for. If the effect you are looking for is actually present in a GR model, it should be present in a model in which the angular momentum of the gravitating system overall can be ignored. So a Schwarzschild exterior with a stationary interior matter distribution should be enough.
"
dark matter models are nothing more than searches for functional fitting forms
"
Yes, but what is being fitted in that case is simply a distribution for the stress-energy tensor, which is already a free parameter in GR. In other words, the assumption is that the actual stress-energy tensor distribution is different from the one that would be inferred solely from the observed distribution of luminous matter, and the fitting is done to see how much different the actual stress-energy tensor distribution has to be to account for the observed rotation curves, using standard assumptions about the effects of spacetime geometry.
That's not what you're doing; you're assuming that the stress-energy tensor distribution is fixed by the distribution of luminous matter, and proposing that the spacetime geometry created by that stress-energy tensor distribution will have effects that differ from the standard assumptions, and that this effects will include a mismatch between the mass inferred from rotation curves and the mass inferred from the distribution of luminous matter. There are no free parameters to fit in such a model. The "fitting" you are doing is based on assumptions about what effects will be present in such a model, without actually constructing it to see if those assumptions are correct.
"
if you deviate from GR, then you lose its divergence-free nature, i.e., you violate local conservation laws (which they readily admit). That's why I wanted to find something in GR proper.
"
I agree that this is a very good reason to want to find a model that works within standard GR.
If you look at what else is being done in this area, you'll see for example the dark matter models are nothing more than searches for functional fitting forms (in that case, a search for the distribution of dark matter). And, as we point out in one of our papers, our ansatz is just as motivated as MOND's. I think modified GR is better theoretically, but even there one can ask, why those particular additions to the Lagrangian? The bottom line is always the same, because they work to fit the data. Of course, if you deviate from GR, then you lose its divergence-free nature, i.e., you violate local conservation laws (which they readily admit). That's why I wanted to find something in GR proper.
Have you done the fits for these data using MOND, various modified gravity theories, and the different DM models?
"
I'm not approaching this from the perspective of trying to do empirical curve fits. Your basic contention is that, if we properly model something like a galaxy using GR instead of a Newtonian approximation, we can explain the discrepancy between the mass inferred from observed galaxy rotation curves and the mass inferred from observed total luminous objects in the galaxy without having to use dark matter. I'm trying to figure out if I agree that some kind of GR model could be constructed that would do that.
You're not exhibiting any such model in the paper; you're just using an ansatz that "looks reasonable" to you and doing empirical curve fitting with it. To me that's backwards. First you would need to construct a GR model–an actual spacetime geometry–that was a viable simplified model for something like a galaxy (i.e., stationary, which, as I have pointed out, the "interior" FRW region in the example you give is not), although obviously it would not be able to capture all the details of a real galaxy. Then you would need to show that this model exhibits the effect you are looking for–that there is a discrepancy between the mass inferred from rotation curves in the model and the mass inferred from observed total luminous objects in the model–and that the size of the effect is of the right rough order of magnitude. Only once you have done that would it be justified, IMO, to extract an ansatz from such a model and use it for empirical curve fitting.
What I'm trying to do for myself is the first two steps I just described: to see if I think there could be a simplified GR model that exhibits the effect in question of the right rough order of magnitude, based on your general description of a difference between "proper mass" and "dynamic mass", but a model whose "interior region" is stationary.
Correct.
"
Ok. One thing about that example that makes it inappropriate for modeling something like galaxy rotation curves is that the "interior" FRW spacetime region cannot be stationary, whereas to model something like a galaxy, you would need an "interior" spacetime region that was stationary. This would also be true for modeling an individual star in a galaxy, but a stationary model for a star is easy: a spherically symmetric blob of matter in hydrostatic equilibrium with a constant surface area. A galaxy is not a continuous distribution of matter, although a really rough approximation could perhaps model it as such; but a better model would be a system of objects orbiting their common center of mass under their mutual gravity. I don't know how much models of that sort have been constructed in the literature; the only one that I can bring to mind at the moment is the one in a paper by Einstein in the 1930s where he was trying to prove that black holes were impossible (of course he didn't use the term "black hole" since it hadn't been invented yet) by showing that no such stationary system of mutually orbiting objects could have an "areal radius" smaller than ##3 G M / c^2##, where ##M## is the externally measured mass of the system. A galaxy of course has a much larger "areal radius" so that wouldn't be an issue for such a model.
Just to be clear, you mean that the spacetime in this solution has a region which is Schwarzschild and a region which is FRW, with a boundary between them, correct?
[Edit: This is in reference to the example in ref. 24 in the article.]
"
Correct.
In order that the DM fits are compelling, we would need to derive theoretical predictions for the fitting factors currently found empirically (for galactic rotation curves, galactic cluster mass profiles, CMB anisotropies) using contributions from those boundary terms. Again, that's just a simplification, but no one is ever going to solve Einstein's equations for a real galaxy. What we need to do is at least motivate the fitting factors via other measurements (luminosity, temperature, etc.). Then check the theoretical (approximated) predictions for the fitting factors against those obtained empirically. The work done to date was simply to find out whether or not the inverse square law functional form is reasonable (the answer there is clearly affirmative), so we know what we're looking for in the GR formalism. Have you done the fits for these data using MOND, various modified gravity theories, and the different DM models? If so, you'll see that our result is on par with all of those (I did all those and showed the comparisons in our papers). Anyway, finding theoretical predictions for the fitting factors should be possible, but I've been working on other questions in foundations that I find more interesting :-)
What I find more interesting than finishing the "no-DM-GR-is-correct model" is showing how the whole of physics is coherent, contrary to popular belief. And, I found a big piece of that by answering Bub's question, "Why the Tsirelson bound?" So, I've been busy these past two years working on the consequences of that answer.
One solution obtained by combining two other solutions.
"
Just to be clear, you mean that the spacetime in this solution has a region which is Schwarzschild and a region which is FRW, with a boundary between them, correct?
[Edit: This is in reference to the example in ref. 24 in the article.]
one and the same matter has two different values of mass — one obtained by inertial observers inside the matter and one obtained by inertial observers in orbit around the matter.
"
I see what you mean, but I still think your language is misleading. An inertial observer in orbit around an object made of matter is not measuring the "dynamic mass" of individual small pieces of matter in the object; he's mesauring the "dynamic mass" of the whole object. He has no way of separating that into individual pieces.
The inertial observer inside the matter, OTOH, is measuring the "proper mass" of the individual piece of matter with which he is co-located. He cannot directly measure the mass of the whole object. He can only calculate it using observations and assumptions.
"
This differs from the usual notion of binding energy
"
In the sense that, in your description, the spacetime is not stationary (since the FRW region cannot be stationary), yes, this is true. However…
"
e.g., a free neutron has one mass and a bound neutron has another mass.
"
…this is stated incorrectly, IMO. A correct statement would be that a system containing bound neutrons (such as an atomic nucleus) has a mass that is smaller than the sum of the free masses of its constituents (for example, the mass of a deuteron is less than the mass of a free proton plus the mass of a free neutron). A measurement of the mass of the bound system cannot be separated into a measurement of the "bound mass" of individual constituents: you can't separate the measured mass of a deuteron into "mass of a bound proton" and "mass of a bound neutron".
After further perusal of the paper, I think the choice of words here is misleading. What is being described in the paper is simply the fact that the externally measured mass of a gravitationally bound system in GR is not equal to the "naive" sum of the masses of its constituents–where "naive" sum means we just add up the locally measured masses of the constituents instead of actually doing a proper integral with a proper integration measure that takes the spacetime geometry into account. The difference between the "naive" sum and the externally measured mass of the system as a whole is usually referred to as "gravitational binding energy".[/quote]
The two different values of mass for one and the same matter are obtained properly using the local metric.
"
All of that is fine, but the phrase "different combined spatiotemporal geometries" is misleading. There is only one spacetime geometry in any given spacetime in GR. [/quote]
One solution obtained by combining two other solutions. Standard GR, nothing misleading here.
"
What I called the "locally measured mass" of a constituent of a gravitationally bound system above is the mass that would be measured by an observer co-located with the constituent, in a local inertial frame in which spacetime curvature can be ignored. But the fact that spacetime curvature can be ignored in such a local measurement does not mean it isn't there; the actual spacetime geometry is still curved, and doesn't change when we go from a local measurement on a single constituent to an external measurement of the system as a whole.[/quote]
Again the meaning of "mass" in the two solutions is unambiguous and intuitive. In the cosmology part, it is just dust density times co-moving volume. In the Schwarzschild part, it is obtained by rotational dynamics. In both cases, the observers are in inertial frames (following geodesics). Again, standard GR, nothing unusual.
"
I also don't think "contextuality for mass" is an appropriate term in this context. All of the measurements being described are invariants; they don't depend on who is measuring them or what other measurements are being done in combination with them. So I don't see any valid analogy with contextuality in QM.
"
Thus, one and the same matter has two different values of mass — one obtained by inertial observers inside the matter and one obtained by inertial observers in orbit around the matter. This differs from the usual notion of binding energy, e.g., a free neutron has one mass and a bound neutron has another mass. In that case, the mass is different at different times, the context changes temporally. Here the mass is different in different regions of space, it is the same in each spatial region at all times. Either way, the mass of matter is clearly a function of the context, thus the phrase.
There is nothing "crank" about this result, it's not like this idea slipped past referees and editors at different journals. No referee or editor has ever questioned the result or the terminology because it comports with GR.
The phrase "matter can simultaneously possess different values of mass when it is responsible for different combined spatiotemporal geometries" doesn't seem correct to me
"
After further perusal of the paper, I think the choice of words here is misleading. What is being described in the paper is simply the fact that the externally measured mass of a gravitationally bound system in GR is not equal to the "naive" sum of the masses of its constituents–where "naive" sum means we just add up the locally measured masses of the constituents instead of actually doing a proper integral with a proper integration measure that takes the spacetime geometry into account. The difference between the "naive" sum and the externally measured mass of the system as a whole is usually referred to as "gravitational binding energy".
All of that is fine, but the phrase "different combined spatiotemporal geometries" is misleading. There is only one spacetime geometry in any given spacetime in GR. What I called the "locally measured mass" of a constituent of a gravitationally bound system above is the mass that would be measured by an observer co-located with the constituent, in a local inertial frame in which spacetime curvature can be ignored. But the fact that spacetime curvature can be ignored in such a local measurement does not mean it isn't there; the actual spacetime geometry is still curved, and doesn't change when we go from a local measurement on a single constituent to an external measurement of the system as a whole.
I also don't think "contextuality for mass" is an appropriate term in this context. All of the measurements being described are invariants; they don't depend on who is measuring them or what other measurements are being done in combination with them. So I don't see any valid analogy with contextuality in QM.
References [23] and [24] make some very bold claims (namely that dark energy and dark matter are chimeras of improper application of GR thus explaining the CMB, galaxy rotation curves, clusters, and dark energy phenomena). Are there any other groups that have concurred in that conclusion?
"
There are lots of other fits, we share some in those papers. No one has anything compelling at this point. I’d like to get back and develop the physics, but I’ve been too busy working on foundations stuff
We then outline how one might extrapolate to theories of quantum gravity based on those principles.
"
Ok, I need to read that part of the Insight more carefully. The phrase "matter can simultaneously possess different values of mass when it is responsible for different combined spatiotemporal geometries" doesn't seem correct to me, but perhaps I'm misunderstanding what it's intended to mean.
You can't possibly know this without a theory of quantum gravity. All you can know without that is that the relationship is valid under conditions where gravity can be ignored.
Not as long as your definition of "foundations of physics" is ok with the fact that claims based on theories that are known to have a limited domain of validity cannot be asserted as valid outside that domain.
"
We can possibly know what is shown deductively in the paper. It's not a matter of opinion, we are stating mathematical and empirical facts. Now, it may be the case that what we are observing and describing mathematically in current experimental situations does not extrapolate to other experimental situations. But, that's the point of physics — to articulate empirically discovered principles/laws/regularities/constraints, extrapolate them theoretically, and test the extrapolations. What we point out in https://www.mdpi.com/1099-4300/22/5/551/pdf is that dd = 0 and the relativity principle that held for Newtonian physics and E&M are still holding in modern physics. We then outline how one might extrapolate to theories of quantum gravity based on those principles. That's one way to use foundations of physics.
The relationship between SR and QM that we point out is valid, so de facto it is independent of gravity.
"
You can't possibly know this without a theory of quantum gravity that has been experimentally confirmed. All you can know without that is that the relationship is valid under conditions where gravity can be ignored.
"
we don't need a theory of everything to do foundations of physics.
"
As long as your definition of "foundations of physics" is ok with the fact that claims based on theories that are known to have a limited domain of validity cannot be asserted as valid outside that domain.
To me, that's because your analysis is limited in scope, which, as I said, doesn't seem viable if you are talking about foundations. For example, your analysis doesn't cover gravity.
"
The relationship between SR and QM that we point out is valid, so de facto it is independent of gravity. Indeed, the principle relating them (relativity principle) and dd = 0 hold across all theories of physics, Newtonian and modern. Thus, it is clear that we don't need a theory of everything to do foundations of physics.
The theoretical structure of GR in no way undermines that relationship and does not add anything to the analysis.
"
To me, that's because your analysis is limited in scope, which, as I said, doesn't seem viable if you are talking about foundations. For example, your analysis doesn't cover gravity.
Perhaps in a practical sense this is true for many problem domains. But you are talking about foundations. For foundations, the fact that GR is more accurate than SR is critical.
We use coordinates to describe the results of measurements. We do not use coordinates to make measurements. Measurement results are invariants. Coordinate values are not.
"
The comparison I'm talking about is the relativity principle of SR as applied to c with its application in QM to h. The theoretical structure of GR in no way undermines that relationship and does not add anything to the analysis. The coordinate values can (and usually do) correspond to or directly relate to measured values, e.g., SG magnet angles. The point of a coordinate system is, as the name states, to "coordinate."
We rarely have to worry about GR corrections.
"
Perhaps in a practical sense this is true for many problem domains. But you are talking about foundations. For foundations, the fact that GR is more accurate than SR is critical.
"
we do use distant coordinates all the time in making measurements, e.g., probes around distant planets
"
We use coordinates to describe the results of measurements. We do not use coordinates to make measurements. Measurement results are invariants. Coordinate values are not.
But there's no unique way of doing that. In SR, if the observer is inertial forever, there is at least a coordinate chart that is picked out by the observer's state of motion–but in our real universe spacetime is not flat and no observer is ever inertial forever.
Only on the observer's worldline. The coordinates picked by an observer on Earth don't represent what the observer directly measures in the Andromeda galaxy since the observer can't directly measure anything there.
"
We rarely have to worry about GR corrections. And we do use distant coordinates all the time in making measurements, e.g., probes around distant planets.
The coordinates are associated with the observer here
"
But there's no unique way of doing that. In SR, if the observer is inertial forever, there is at least a coordinate chart that is picked out by the observer's state of motion–but in our real universe spacetime is not flat and no observer is ever inertial forever.
"
they certainly do have physical meaning for the observer, they represent what that observer will measure.
"
Only on the observer's worldline. The coordinates picked by an observer on Earth don't represent what the observer directly measures in the Andromeda galaxy since the observer can't directly measure anything there.
No, it's coordinate dependent. Which means that, according to the standard way that GR is interpreted, it has no physical meaning, since only invariants have physical meaning.
"
The coordinates are associated with the observer here and they certainly do have physical meaning for the observer, they represent what that observer will measure.
I'm talking about partitions per surfaces of simultaneity for any given observer.
"
Yes, I know that.
"
The partition I'm talking about is therefore observer dependent
"
No, it's coordinate dependent. Which means that, according to the standard way that GR is interpreted, it has no physical meaning, since only invariants have physical meaning.
Relativity does not partition spacetime into two regions with respect to a particular event. It partitions spacetime into three regions: the past light cone, the future light cone, and the spacelike separated region. This partitioning, for any given event, is invariant.
It seems to me that the above fact should be taken into account in any attempt to provide an explanation.
"
That is a different partition altogether. I'm talking about partitions per surfaces of simultaneity for any given observer. The partition I'm talking about is therefore observer dependent, which is key to the entire explanation.
relativity of simultaneity (different partitions of spacetime)
"
Relativity does not partition spacetime into two regions with respect to a particular event. It partitions spacetime into three regions: the past light cone, the future light cone, and the spacelike separated region. This partitioning, for any given event, is invariant.
It seems to me that the above fact should be taken into account in any attempt to provide an explanation.
I've started a thread in the BSM forum zeroing in only on the subtopic of a discussion of references [23] and [24] in the Insights article. https://www.physicsforums.com/threa…d-dark-energy-with-minor-tweaks-to-gr.994343/
"
Moderator's note: That thread has been put in moderation for review. On an initial look, it is much too long and much too broad for a single thread discussion; a single thread discussion should be focused on one particular reference, and ideally on one particular question raised by that reference.
Also, that thread is asking for people's "gut check" opinions, which is off topic and doesn't lead to fruitful discussion.
hmm. I sort of read the table in the article up and down and that's why "at least both are chickens" aha. And I guess I see NPRF as exactly that pretty neat coincidence between relativity of simultaneity and the discrete partitioning of information for Bell observers in different frames.
to me these sound like accurate historical accounts of "what happened"
So, I guess I see NPRF as a statement of "connected fact" rather than pejorative "amazing coincidence".
"
That could be true
I’m going to go with “partition”, and venture even further… that is what physical chemistry sort of is.
"
Let's look at SR. Here is the explanatory hierarchy as we present it in our paper:
NPRF –> everyone measures c –> time dilation and length contraction –> relativity of simultaneity (different partitions of spacetime).
So, NPRF is not the equivalence relation, but it is the ultimate basis for our equivalence relation, which is strictly speaking the synchronized proper time of the comoving observers for either Alice or Bob (or … ). Here we have NPRF/equivalence relation leading to the partition. Now let's flip it:
Relativity of simultaneity –> time dilation and length contraction –> everyone measures c –> NPRF.
For QM we have:
NPRF –> everyone measures h –> average-only conservation and Bell state correlations –> relativity of data partition (different partitions of Bell state data).
Again, NPRF isn't the equivalence relation, but it is the ultimate basis for it. Now let's flip it:
Relativity of data partition –> average-only conservation and Bell state correlations –> everyone measures h –> NPRF.
If you go with the equivalence relation as fundamental, you have one and the same rule leading to two different consequences. If you go the other way, you have two different rules with the exact same consequence. I think physicists would prefer the former, since they tend to be reductionists (explain more and more with less and less" per Weinberg). The other way makes NPRF look like an amazing coincidence.
Which comes first, the partition that provides the correct equivalence relation on average for (c,h,G, b?) or the equivalence relation that dictates partition?
"
Which is the superselection rule as you see it?
I enjoyed this, esp the image of other universal constants working the same as c.
it seems like a chicken and egg problem a little (QM superselection rules and NPRF physical constants) but at least they are both chickens.
"
Thnx. Would you mind expanding on that second comment for me? A referee said something similar, so I'm curious what exactly brought that to mind