Significant Figures: Rounding Rules & Examples for Science

Definition / Summary

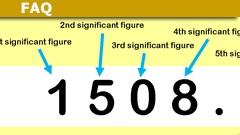
Significant figures (commonly called “sig figs”) are the digits in a number that are considered when rounding a value to reflect its precision. They show how accurately a quantity is known.

Examples: Rounding to significant figures

For example, the number 789.001 rounded to 6, 5, 4, 3, 2 and 1 significant figures becomes:

• 6 sig figs: 789.001
• 5 sig figs: 789.00
• 4 sig figs: 789.0
• 3 sig figs: 789
• 2 sig figs: 790
• 1 sig fig: 800

Comparison: decimal-place rounding

By comparison, rounding the same value to decimal places (digits after the decimal point) gives:

• 3 decimal places: 789.001
• 2 decimal places: 789.00
• 1 decimal place: 789.0

Basic rules

Rules for arithmetic operations

• Multiplication & division: Round the final result to the same number of significant figures as the input with the fewest sig figs.
• Addition & subtraction: Round the final result to the same decimal place (same place value) as the least precise input — i.e., the highest (largest) place value among the inputs.
• Intermediate steps: Keep extra digits during intermediate calculations and round only the final result to avoid cumulative rounding error.

Extended explanation

Multiplying and dividing

When multiplying or dividing, the limit on precision comes from the number with the fewest significant figures. Round the final answer to that many significant figures.

Adding and subtracting

For addition or subtraction, precision is limited by the input with the largest place value (the least precise decimal place). Round the result to that decimal place.

Whole-number trailing zeros

Special case for whole numbers that end with zeros: if an input is a whole number like 5,700 or 5,000, consider the number of trailing zeros as indicating its precision when that precision is implied. Use the largest number of trailing zeros among whole-number inputs when determining the rounding place.

Examples:

Examples: whole-number trailing zeros

• 571000 + 5300 = 576000 (uses the largest number of trailing zeros)
• 500000 + 5300 = 500000 (500000 dominates because it is only known to the hundred-thousand place)
• 571320 + 5300 = 576900 (results rounded to the same place value)

Examples: addition/subtraction with decimals

• 5.71 + 2351.2 = 2356.9
• 5.7 + 2351.21 = 2356.9
• 5.7 + 2351 = 2357
• 5.7 + 2350 = 2360

Common sense & measurement context

How you round often depends on how a quantity was measured. Consider this example:

Car-speed example

If a car takes 890.3 seconds to travel 50 kilometres, the exact calculation gives about 56.16084… m/s. How you round that value depends on the precision of the 50 km measurement:

• If the distance came from a map and is only accurate to the nearest 1 km (written as “50”), you might treat that as two significant figures and report the speed as approximately 56 m/s.
• If the distance came from the car’s odometer and is accurate to the nearest 0.1 km, you could treat it as three significant figures and report the speed as 56.2 m/s.
• If the distance was an imprecise estimate (for example, a long offshore distance without GPS), you might treat it as one significant figure and report the speed as 60 m/s.

Ignoring the unit precision (measured vs. reported)

If a value is reported with more digits because it was measured precisely (for example, “50.000 km”), then you should use that precision. Conversely, if a number is given as a defined value or exact count (for example, 1 minute = 60 seconds exactly or “5 items”), it has effectively infinite precision for the purpose of significant-figure rules.

Example: time and distance precision

Example rephrased: if you are told an object moved 23.77 metres in 1 second, you would not round the speed to 20 m/s just because the “1 second” is written with one digit — you’d usually assume the time measurement is accurate enough or was measured to match the distance precision, so you would report 23.77 m/s unless told otherwise.

Rounding around powers of ten (just above 10^n)

Applying a strict sig-fig rule can give odd results near scale boundaries. For example, if you are told to report values to 2 sig figs, four speeds of 99.31, 99.51, 100.51 and 105.51 m/s would round to:

Example list: boundary rounding

• 99.31 → 99
• 99.51 → 100
• 100.51 → 100
• 105.51 → 110

That result (99, 100, 100, 110) can be misleading because adjacent values become identical. Common-sense judgment is required: sometimes it’s better to round all values to the same number of decimal places or the same place value (for example, to 0 decimal places) so the sequence becomes 99, 100, 101, 106 — which preserves the order and meaning better. Deciding when to change rounding strategy is a matter of judgment and context.

Further reading

• 10 Math Tips to Save Time & Avoid Mistakes
• Frequently Made Errors in Equation Handling
• Comment thread: What are significant figures?