Tangent Line and Hyperplane: Definitions & Circle Example

Definition / Summary

Informal idea

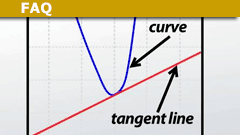
The tangent to a curve in a plane at a particular point has the same gradient as the curve at that point.

Generalization

More generally, the (n−1)-dimensional tangent hyperplane to an (n−1)-dimensional surface in n-dimensional space at a particular point has the same gradient (the same first-order linear approximation) as the surface at that point.

Implicit surface: tangent hyperplane

Let A = (a1, a2, …, an) be a point on a surface defined implicitly by F(x1, x2, …, xn) = 0. The tangent hyperplane to the surface at A is:

Tangent hyperplane equation

(∂F/∂x1)|_A · (x1 − a1) + (∂F/∂x2)|_A · (x2 − a2) + … + (∂F/∂xn)|_A · (xn − an) = 0.

Parametric curve: tangent line

If a curve in n dimensions is defined by a parameter t as A(t) = (a1(t), a2(t), …, an(t)), then the tangent line at t0 is given in vector form by

Vector form

x = A(t0) + s · A'(t0),

where A'(t0) = (da1/dt, da2/dt, …, dan/dt) evaluated at t0 and s is a scalar parameter.

Component ratios

Equivalently (when none of the components of A'(t0) are zero) you can write the component ratios

(x1 − a1(t0)) / a1′(t0) = (x2 − a2(t0)) / a2′(t0) = … = (xn − an(t0)) / an'(t0).

Circle example

Implicit form and partial derivatives

Circle equation

For example, let A = (x0, y0) lie on the circle with center (p, q) and radius r, defined by

F(x, y) = (x − p)² + (y − q)² − r² = 0. (1)

Partial derivatives

The partial derivatives at A are

(∂F/∂x)|_A = 2(x0 − p),

(∂F/∂y)|_A = 2(y0 − q).

Equation of the tangent (implicit form)

Using tangent hyperplane

Using the tangent hyperplane formula, the tangent line at A is

(x0 − p)(x − x0) + (y0 − q)(y − y0) = 0. (2)

Parametric form of the circle and tangent

Parametrization

The same circle can be parameterized by A(θ) = (p + r cos θ, q + r sin θ). The tangent at A(θ) can be written (assuming r ≠ 0) as

Tangent ratios

(x − p − r cos θ)/(−r sin θ) = (y − q − r sin θ)/(r cos θ).

Derivation: an alternate, memorable form

Point on circle

Let M = (x1, y1) be a point on the circle K. Then M satisfies the circle equation

(x1 − p)² + (y1 − q)² = r². (3)

Tangent at M

The tangent at M (from (2)) is

(x1 − p)(x − x1) + (y1 − q)(y − y1) = 0.

Combine equations

If you add (3) to that tangent equation you obtain

(x1 − p)(x − x1) + (y1 − q)(y − y1) + (x1 − p)² + (y1 − q)² = r²,

Final form

which simplifies to

(x1 − p)(x − p) + (y1 − q)(y − q) = r². (4)

Equation (4) is an alternate form of the tangent line at M(x1, y1) ∈ K that is often convenient for algebraic manipulations.

Special case: circle centered at the origin

If the circle K has center (0, 0) so it is x² + y² = r², then p = q = 0 and (4) becomes the compact form

x1·x + y1·y = r².

Further reading

References

See also https://www.physicsforums.com/insights/the-pantheon-of-derivatives-i/ and the list at the beginning of https://www.physicsforums.com/insights/journey-manifold-su2mathbbc-part/ where different views of the derivative are discussed — the slope isn’t even among them in that survey.

Comment Thread