Curves Definition and 741 Threads
-

Drawing Surfaces & Space Curves
Homework Statement Drawing surface ##f(x,y) = ...## or ##r(t) = <f(t),g(t)>## etc. The Attempt at a Solution I've been working on drawing space curves lately, by breaking into separate planes and by level curves. I'm struggling w/ this topic. (1) If I'm not mistaken, this is fundamental in...- vanceEE
- Thread
- Curves Drawing Space Surfaces
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

High School Strategies for drawing space curves?
What are some helpful strategies for drawing and conceptualizing space curves? I'm having trouble drawing them and I'm not very artistic! Also, please provide helpful videos on this topic if you can. Thanks. -
D
Graduate Can Space Curve Without Mass or Energy?
Is there such a thing as a spatial field containing energy or mass? How do you bend something without either? -
J
Finding the area between Polar Curves
Homework Statement Find the area of the region that consists of all points that lie within the circle r = 1 but outside the polar equation r = cos(2θ) Homework Equations A = ∫ 1/2 (r2^2 - r1^2) dθ, where r2 is outer curve and r1 is inner curve. The Attempt at a Solution Here is...- jojo13
- Thread
- Area Curves Polar
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

MHB Find Intersections of y=sin(x) and y=1-x^2 | Mangoqueen54
Here is the question: I have posted a link there to this thread so the OP can view my work.- MarkFL
- Thread
- Curves Intersection Points
- Replies: 1
- Forum: General Math
-
R
Slopes of tangent lines of parametric curves.
1. The problem statement,ll variables and given/known data I have the first and second derivatives of a parametric function and the book is asking for when the slope of the tangent is vertical and horizontal. I get that horizontal is when dy/dx is 0. But what about vertical, is that dy/dx is 1...- rmiller70015
- Thread
- Curves Lines Parametric Tangent
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-

MHB Roxy's question at Yahoo Answers regarding finding the area between two curves
Here is the question: I have posted a link there to this thread so the OP can view my work. -

Show that differentiable curves have measure zero in R^2
Homework Statement (a) Let \alpha:I=[a,b]→R^2 be a differentiable curve. Assume the parametrization is arc length. Show that for s_{1},s_{2}\in I, |\alpha(s_{1})-\alpha(s_{2})|≤|s_{1}-s_{2}| holds. (b) Use the previous part to show that given \epsilon >0 there are finitely many two...- Demon117
- Thread
- Curves Differentiable Measure Zero
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
R
Graduate Comparing curves using gaussian process regression
Hi guys, I have run multiple simulations on networks that are all slightly perturbed from each other. They produce slightly different curve outputs onto an x-y graph which I need to now analyse (it has been about 5 years since I did statistical analysis hence why I am here). A couple of the...- rp8308
- Thread
- Curves Gaussian Gaussian process Process Regression
- Replies: 11
- Forum: Set Theory, Logic, Probability, Statistics
-
J
What Shape Do the Characteristic Curves of This PDE Form?
Homework Statement suppose u(x,y) satisfies the partial differential equation: -4y\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}=0 Find the characteristic curves for this equation and name the shape they form The Attempt at a Solution \frac{dy}{dt}=1 \Longrightarrow y=t+y_0...- jimmycricket
- Thread
- Characteristic Curves Pde Shape
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
M
MHB Integrate the function f at the path that consists of the curves C1 and C2
Hey! :o I have the following exercise: Integrate the function $f=x+ \sqrt{y} -z^2$ at the path from $(0,0,0)$ to$(1,1,1)$ that consists of the curves $C_1:r(t)=t \hat{ \imath}+t^2\hat{ \jmath}, 0 \leq t \leq 1$ and $C_2: r(t)=\hat{ \imath}+\hat{ \jmath}+t \hat{k}, 0\leq t \leq1$.My solution is... -
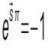
Graduate Originary Curves: Mathematical & Physical Properties
We call originary curve the curve for that at baseline the Frenet trihedron TNB coincides with the cartesian trihedron IJK. Therefore, the originary curve is the curve that passes through the origin of the cartesian landmark and for that at the origin the tangent vector to the curve coincides...- Abel Cavaşi
- Thread
- Curves
- Replies: 5
- Forum: Differential Geometry
-
N
Undergrad Determining if 3 curves have the same period
Suppose there are 3 different curves. How do I determine if they have the same period? I am aware of how to calculate period but how do we determine if they have the same period graphically? 1) what is the idea behind x(t) = x(t+T)? 2) must all 3 curves cuts a particular horizontal at...- negation
- Thread
- Curves Period
- Replies: 2
- Forum: Other Physics Topics
-
S
How Does Conformal Transformation Affect Curve Types in General Relativity?
Hi. This problem is about General Relativity. I am not actually taking a course, but studying myself. I tried to solve Hobson 2.7: Homework Statement A conformal transformation is not a change of coordinates but an actual change in the geometry of a manifold such that the metric tensor...- spookyfish
- Thread
- Curves
- Replies: 3
- Forum: Advanced Physics Homework Help
-
R
How Do You Solve the Areas Between Curves Problem Involving Unknown Functions?
Homework Statement Let a > 0 be a fixed real number. Define A to be the area bounded between y=x2,y=2x2, and y=a2. Define B to be the area between y = x2, y = f(x), and x = a where f(x) is an unknown function. a) Show that if f(0) = 0, f(x) ≤ x2, and A = B then int 0-->a2 [y1/2-(y/2)1/2] dy =...- robertmatthew
- Thread
- Areas Curves
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
D
Undergrad How do I find the length of a curve using calculus?
I am just learning how to find lengths of curves using calculus. √((dx)2+(dy)2)→∫√(1+(dy)2)dx. My question is how are you able to bring out the dx. Is this some sort of algebraic trick I've never heard of. Can someone please explain this to me? -
N
MHB Area under curves and Limit of a sequence,
Hello, I am looking for an help about this, I have very short time to do many of them and those are an example, could someone show me one solution or explain me how to do it? Thank you if you can help me, I really appreciate. Francesco.- namerequired
- Thread
- Area Curves Limit Sequence
- Replies: 3
- Forum: Calculus
-
B
Finding the Area Bounded by Curves | Quick Solution
Hello, quick question really. Homework Statement Find the area bound by the x axis, x = 1, x = 4 and y = 2/x Homework Equations The Attempt at a Solution Representing this graphically, the question is equivalent to performing the definite integral of y = 2/x from 1 to 4. Right? Which...- BOAS
- Thread
- Area Bounded Curves
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
S
MHB Finding the area bounded by the curves
So it's been a while since I've done one of these problems. Need to make sure I am using the right procedures to solve it. Q)Find the area bounded by the curve $y = \frac{1}{2}x^2$ and $x^2 + y^2 = 8$ So first thing I did was plug in numbers to get the two graphs. It looks like they intersect... -
A
Undergrad Level curves (or contour curves) of a certain 3 dimensional function.
I can't seem to quite comprehend the level curves for f(x,y)=xy. I realize this should be very simple yet the answer eludes me. f(x,y) for this the two dimensional representation of this function will be substituted with k(a fixed number). I would greatly appreciate somebody explaining my... -
B
Integral Question: Areas between curves?
Homework Statement Sketch the region in the first quadrant enclosed by the given curves. Decide whether to integrate with respect to x or y. Then find the area of the region. y=4cosx, y=6sin2x, x=0. Homework Equations The Attempt at a Solution I got the intersections, which...- baquid
- Thread
- Areas Curves Integral
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
Y
MHB Level curves: true / false question
Hello again, I have another level curves related question, which I tried solving, but I have the feeling that I did something wrong, would appreciate it if you could have a look. The question is: The function f is given by: \[f(x,y)=x^{2}+\sqrt{x+2y}\]C1 is the level curve that goes through... -
Y
Maple Exploring Level Curves of a Function with Maple
Hello all, I am trying to draw the level curves of this function: \[z=\frac{x^{2}+y^{2}}{y}\] at C=-1,-2,1,2 I started with C=1, and I got kind of stuck with this shape \[x^{2}+y^{2}=y\] Maple gave this as the answer, I don't get it: thanks !- Yankel
- Thread
- Curves Function Maple
- Replies: 3
- Forum: MATLAB, Maple, Mathematica, LaTeX
-
J
1st and 2nd moment of interia of curves and surfaces
If I can to calculate the 1st and 2st moment of inertia of areas and volumes, I can compute for curves and surfaces too?- Jhenrique
- Thread
- Curves Moment Surfaces
- Replies: 2
- Forum: General Engineering
-
E
Help - How to obtain rocking curves?
Help -- How to obtain rocking curves? Hello everyone! I'm happy to have found this forum, I hope you would help me. I need to obtain rocking curves from diffraction spots derived from a 3D X-Rays diffraction test. I've never touched this subject up to now, can somebody give me some...- ErnFrench
- Thread
- Curves
- Replies: 1
- Forum: Materials and Chemical Engineering
-
K
Graduate Stability of Closed Time-Like Curves: Current Status?
I remember reading something, long ago, to the effect that any attempt at creating a CTC would be doomed by energy from vacuum fluctuations piling up through it and leading to explosive behavior (I think the idea originated in work done by Misner and Taub in 1969?). Does anyone know what is...- ksy
- Thread
- Closed Curves Stability Time
- Replies: 4
- Forum: Special and General Relativity
-

Can Differentiation Under the Integral Sign Solve Regular Curves Family Length?
Homework Statement Let \alpha : I =[a,b]→R^{2} be a rgular curve parametrized by arc length s. Let f:I→R be a differentiable function with f(a)=f(b)=0. For small values of \epsilon \alpha_{\epsilon}:=\alpha (s) + \epsilon f(s) N(s) defines a one parameter family of regular curves...- Demon117
- Thread
- Curves Regular
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
S
Graduate Understanding Contractible Curves
I read some text to find it's definition Is it possible to tell me it's definition? I read below statements about local and global geometry and I didn't understand it. is it possible tell me it. "If M ( a manifold) has a trivial topology, a single neighborhood can be extended globally...- sadegh4137
- Thread
- Curves
- Replies: 2
- Forum: Topology and Analysis
-

MHB Calculating the Area Between Two Curves: A Shorter Method?
Problem: Calculate the area of region defined by the inequalities: $$-1<xy<1$$ $$-1<x^2-y^2<1$$ Attempt: Although I have solved the problem but I am not very satisfied with the method I used. The graph of region is symmetrical in all the four quadrants so I calculated the area in the first... -
T
Really Challenging Area Between Curves Problem
Homework Statement Suppose C:y=f(x) with f a twice-differentiable function such that f''(x)> 0 for each x on the closed interval [0,a] where a is a positive constant. Suppose T is the tangent line to C at a point P= (r,f(r)) on C where r is in the open interval (0,a). Let A be the area of the...- TheIdealist
- Thread
- Area Curves
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
D
MATLAB Plotting Gaussian Curves with Matlab
Matlab rook here, Suppose I'd want to plot the Gaussian for 10 different values for n:function gauss(c,n) = plot_gaussian.m x=-1*c:0.1:c; gauss(x,j)=sqrt(j./pi)*exp(-1*j.*x.^2); for j=1:n plot(x,y) end And then I'll type gauss(3,10) to plot 10 curves in the interval [-3,3] Also, if I'd...- Dr_Pill
- Thread
- Curves Gaussian Matlab Plotting
- Replies: 1
- Forum: MATLAB, Maple, Mathematica, LaTeX
-
A
Negative area between two curves
I've been trying to figure out what a negative area means, but I can't. Homework Statement Calculate the area between f(x) = 3^{x} \, , \, g(x)=2x+1 The attempt to a solution The intersections are located in x=0 and x=1. So I do the integral from 0 to 1. \int_{0}^{1} (g(x)-f(x))dx =...- adriaat
- Thread
- Area Curves Negative
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
S
Creating lung compliance curves but I'm terrible at the math/graphing
Homework Statement I am trying to replicate the curves in the attachment, but since I am a physiologist it has been quite a while since I've done graphing. I am simply looking for an easy way to replicate these three curves. This is for a practice exam I am creating for first year medical...- sozme
- Thread
- Compliance Curves
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
R
Graduate Hyperbolic geometry - relations between lines, curves, and hyperbolas
Hi. I studied calculus a while back but am far from a math god. I have been reading around online about hyperbolic geometry in my spare time and had a simple question about the topic. If a straight line in Euclidean geometry is a hyperbola in the hyperbolic plane (do I have that right?)...- Reuel
- Thread
- Curves Geometry hyperbolas Hyperbolic Lines Relations
- Replies: 2
- Forum: Differential Geometry
-
T
Shift Equlibrium Concentrations Curves w/o Adding Stress
Hi guys, I have been wondering if its possible to alter equilibrium concentrations without adding stress to the system? Thanks, Larry- tsaitea
- Thread
- Curves Equlibrium Shift Stress
- Replies: 5
- Forum: Biology and Chemistry Homework Help
-
K
How Do You Analyze the Function \( f(x) = \frac{x-4}{x^3} \)?
Homework Statement I am to explain all intercepts, critical numbers, extrema, inflection points, and asymptotes of the function f(x)=(x-4)/x^3. 2. The attempt at a solution a) The y-intercept does not exist, as the domain of the function is all real numbers except x=0. Solving the...- kald13
- Thread
- Curves Graphing Limits
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

MHB Orthogonal trajectories of curves
Hello ! I have to find the orthogonal trajectories of the curves : x^{2}-y^{2}=c , x^{2}+y^{2}+2cy=1 .. How can I do this?? For this: x^{2}-y^{2}=c I found \left | y \right |=\frac{M}{\left | x \right |} ,and for this: x^{2}+y^{2}+2cy=1 ,I found: y=Ax-D,c,A,D \varepsilon \Re ...- evinda
- Thread
- Curves Orthogonal Trajectories
- Replies: 6
- Forum: Differential Equations
-
M
No problem, glad I could help!
Find the values of c such that the area of the region bounded by the parabolas y = x2 - c2 and y = c2 - x2 is 576. Attempt: 576 = -cc∫-x2 + c2 - (x2 - c2) dx 576 = 2-cc∫c2 - x2 dx 576 = c2x -(1/3)(x3) l0c *I know by symmetry that the area of 0 → c is half the area of -c → c 576 = c3 -...- MathewsMD
- Thread
- Area Curves
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
P
Intersection of Two Curves: Do They Meet?
Homework Statement Show that these curves do not intersect. z=(1/a)(a-y)^2 y^2+z^2=a^2/4 Where a is the radius of the circle and other shape. Homework Equations There aren't any. The Attempt at a Solution I tried setting them equal to each other but got the equation...- PensNAS
- Thread
- Curves Intersection
- Replies: 13
- Forum: Calculus and Beyond Homework Help
-

MHB Anonymous' question at Yahoo Answers regarding the area bounded by two curves
Here is the question: I have posted a link there to this thread so the OP can see my work. -
A
Projection of space curves onto general planes
So I've encountered many "what is the projection of the space curve C onto the xy-plane?" type of problems, but I recently came across a "what is the project of the space curve C onto this specific plane P?" type of question and wasn't sure how to proceed. The internet didn't yield me answers so...- Antiderivative
- Thread
- Curves General Planes Projection Space
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
J
Graduate Moment of Inertia of Curves and Surfaces
Greetings! I enjoyed the definition of moment of inertia for a volume and for an area in the form of matrix. It's very enlightening! I = \int \begin{bmatrix} y^2+z^2 & -xy & -xz\\ -yx & x^2+z^2 & -yz\\ -zx & -zy & x^2+y^2 \end{bmatrix}dxdydz '->... -
T
Graduate Mechanism by which mass curves space
Hi everybody. This will be my first post here on PF. :) I'm wondering about the mechanism by which mass causes space to warp and curve within General Relativity. I did a cursory search on the subject and did come across some brief discussion here from a few years ago. At the time, the question...- taicleis
- Thread
- Curves Mass Mechanism Space
- Replies: 9
- Forum: Special and General Relativity
-
L
Curves on surfaces (differential geometry)
A few topics we are covering in class are: Gauss map, Gauss curvature, normal curvature, shape operator, principal curvature. I am having difficulty understanding the concepts of curves on surfaces. For example, this problem: Define the map ##\pi : (\mathbb{R}^3-\{(0,0,0)\})\to S^2## by...- Lee33
- Thread
- Curves Differential geometry Geometry Surfaces
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
L
Unit Speed Curves: Showing Frenet Frames Agree at s
Homework Statement Let ##\alpha(s)## and ##\beta(s)## be two unit speed curves and assume that ##\kappa_{\alpha}(s)=\kappa_{\beta}(s)## and ##\tau_{\alpha}(s)=\tau_{\beta}(s)##, where ##\kappa## and ##\tau## are respectively the curvature and torsion. Let ##J(s) = T_{\alpha}(s)\dot\...- Lee33
- Thread
- Curves Speed Unit
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
1
Partial Derivative Signs Through Level Curves
Homework Statement Question 2 from http://math.berkeley.edu/~mcivor/math53su11/solutions/hw6solution.pdf here. I do not understand b) and e). How do I think of the slope with respect to y? Homework Equations The Attempt at a Solution I do know that the partial derivatives are...- 1question
- Thread
- Curves Derivative Partial Partial derivative
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
1
How to draw graphs and level curves?
Homework Statement f(x,y,z) = 4x^2 + y^2 + 9z^2 another one is xy+z^2 how do u draw level curves and graphs for these? Homework Equations The Attempt at a Solution Just need somewhere to start Thanks- 1LastTry
- Thread
- Curves Graphs
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
G
Stokes theorem, parametrizing composite curves
Homework Statement Calculate the line integral: F = <xz, (xy2 + 2z), (xy + z)> along the curve given by: 1) x = 0, y2 + z2 = 1, z > 0, y: -1 → 1 2) z = 0, x + y = 1, y: 1→0 3) z = 0, x-y = 1, y: 0 → -1 Homework Equations The Attempt at a Solution I don't think the...- Gauss M.D.
- Thread
- Composite Curves Stokes Stokes theorem Theorem
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
J
Undergrad Question about Acceleration and rounding curves
So I've just been a bit confused over the concept of rounding curves and accelerating. Obviously its commonly understood that you need an acceleration to maintain a constant speed when rounding a curve, such as turning a vehicle right, left, or making a u turn. Can anyone help explain why...- Justincase_
- Thread
- Acceleration Curves
- Replies: 4
- Forum: Mechanics
-
Y
Area between two curves integral
Homework Statement Consider the region enclosed by the curves x=2-y^2 and y=-x Write a single integral that can be used to evaluate the area of the region. Find this area. Your answer should be a fraction reduced to its lowest terms. Homework Equations NA The Attempt at a Solution First...- Yosty22
- Thread
- Area Curves Integral
- Replies: 4
- Forum: Calculus and Beyond Homework Help